实录 | 平安人寿资深算法工程师谢舒翼：智能问答系统探索与实践

3 月 14 日（周四）晚 8 点，平安人寿智能平台团队资深算法工程师谢舒翼在 PaperWeekly 直播间为大家带来了智能问答系统的探索与实践主题分享，并且介绍了平安人寿基于业务场景的技术探索成果。

本文将独家分享本期活动的视频实录和嘉宾课件下载。

分享提纲

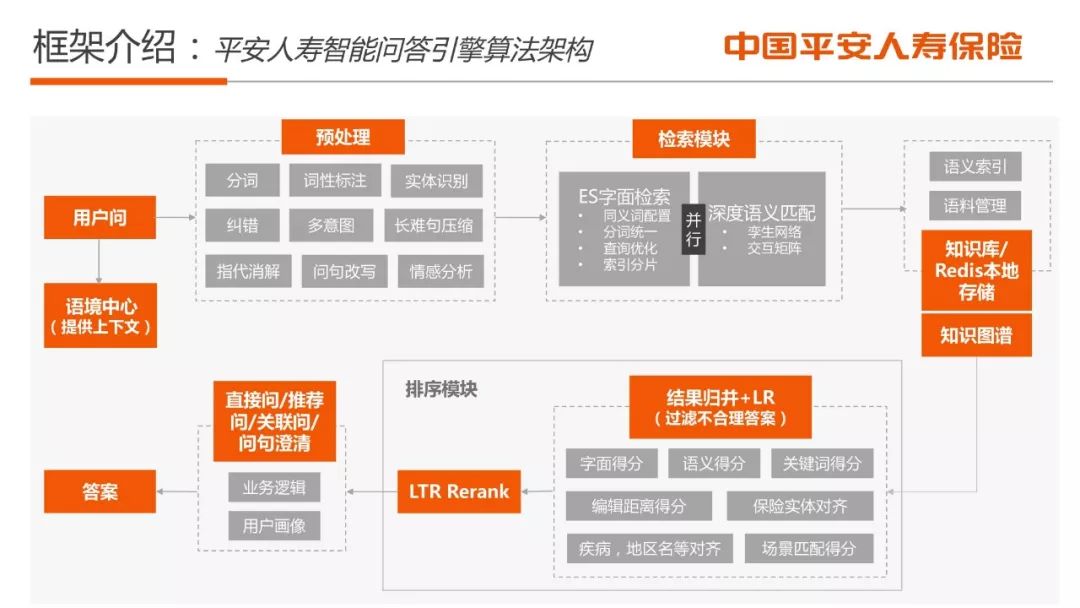
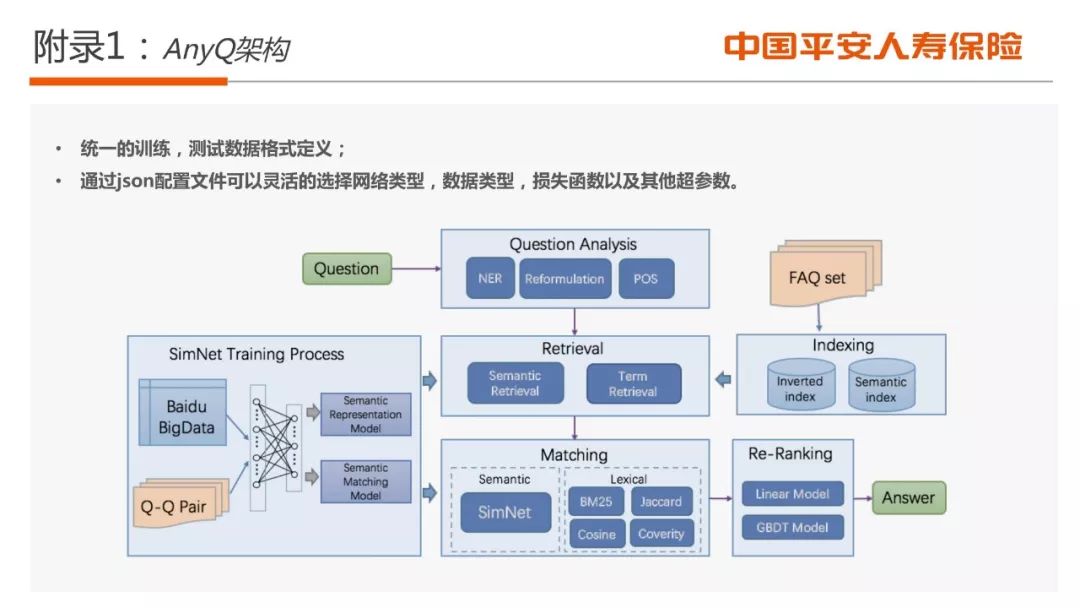
■ 寿险的智能问答系统整体框架介绍； 

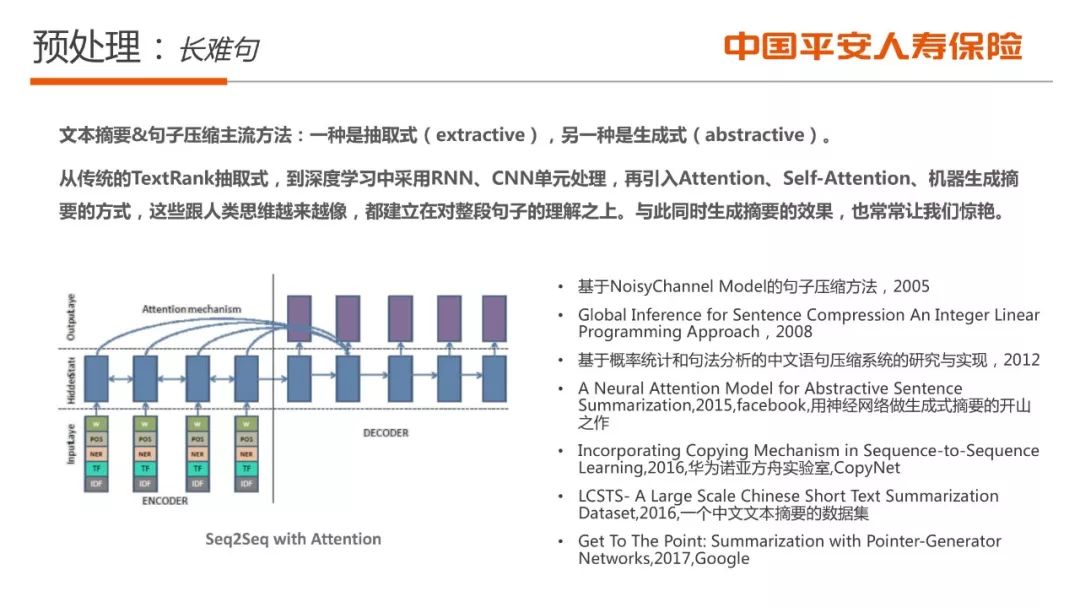
■ 问句预处理核心技术；

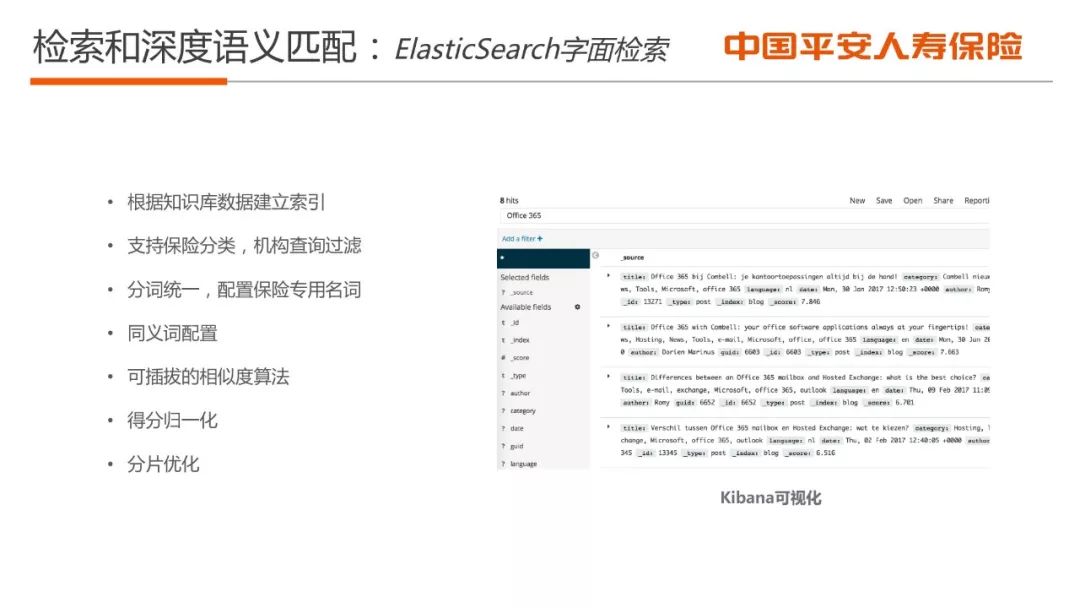
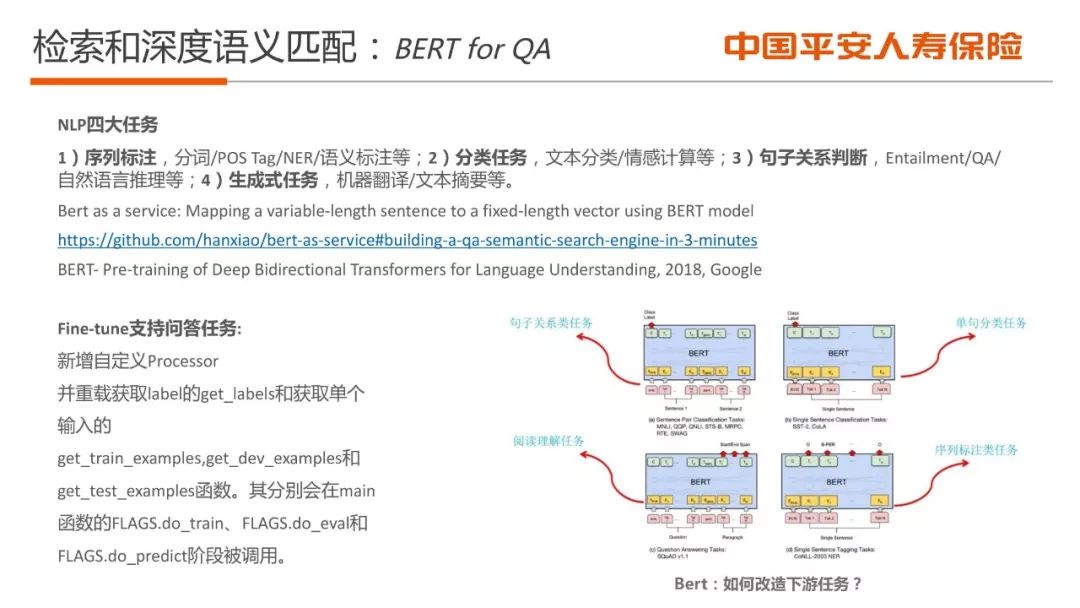
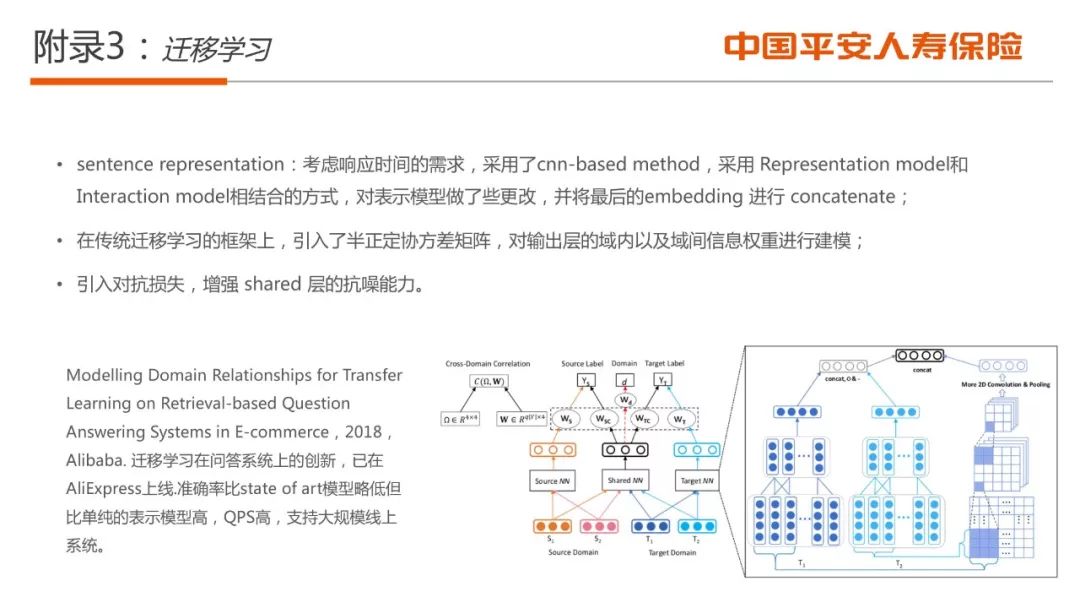
■ 检索和深度语义匹配技术；

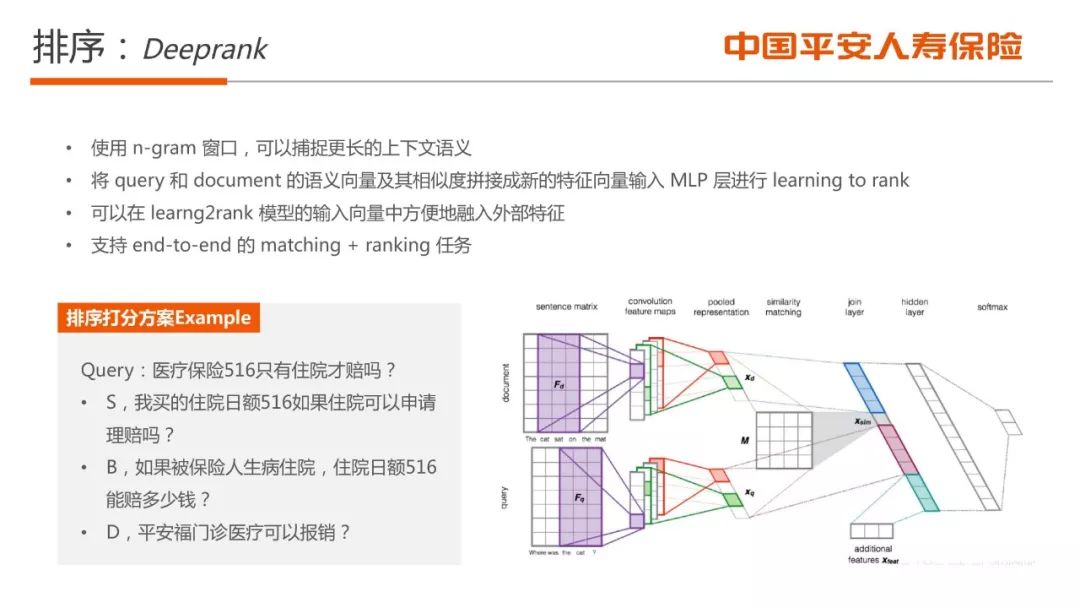
■ 基于深度学习的问答排序算法介绍；

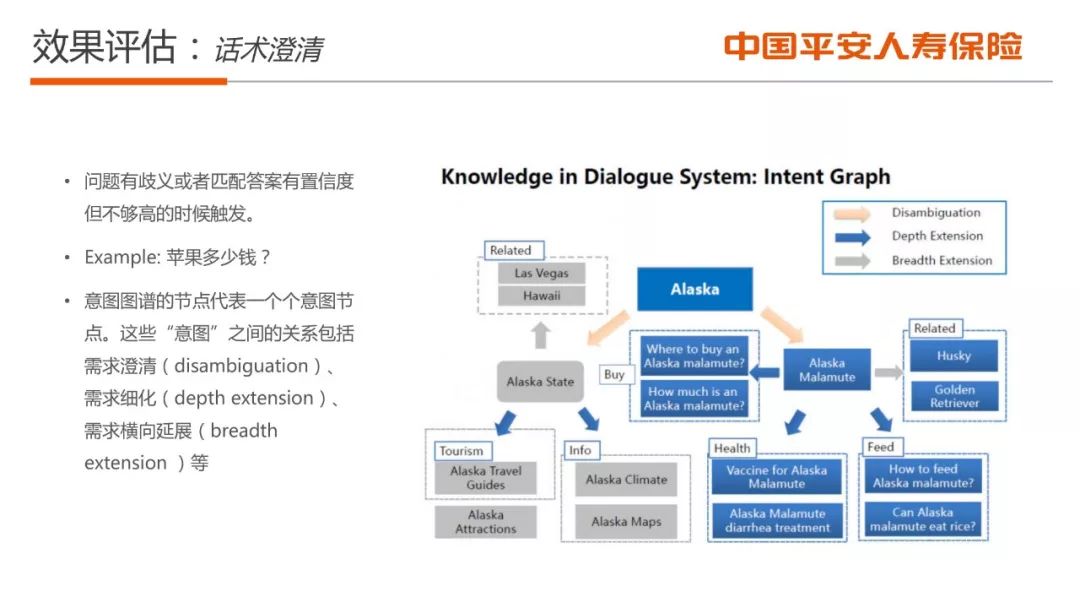
■ 算法效果评估方案。

嘉宾介绍

 谢舒翼 

谢舒翼，平安人寿智能平台团队资深算法工程师。北航计算机系本硕，ACMer，Topcoder，多次获得各类编程赛冠军、数学竞赛一等奖。曾在百度、MSRA 实习，任职于阿里巴巴，现为平安人寿智能平台团队资深算法工程师，主要研究方向为智能问答系统、知识图谱、NLP 相关算法。

实录获取

 1 / 扫码关注 

长按识别二维码，关注PaperWeekly

 2 / 回复暗号 

在后台回复 “ 智能问答” 即可获取下载链接

团队介绍

随着大数据、人工智能等新技术的蓬勃发展，保险行业亦寻求新突破，“保险科技”已成为行业新兴战场。一方面，保险业大量的数据积累提供了丰富的场景；另一方面，AI 技术的应用也为行业发展注入了新的动力。 

平安人寿智能平台团队，致力于人工智能研究以及前沿技术在招聘、培训、服务、销售、风控等保险业务中的应用。团队成员聚焦于深度学习、自然语言处理、人机交互、智能推荐、计算机视觉等研究领域，目前已自主研发了面试机器人、客服机器人、培训机器人等，并搭建了行业领先的人机交互应用平台及分布式深度学习平台。人工智能的加速赋能已成为平安人寿的核心竞争力之一，其 AI 技术突破与应用效果不断获得各界认可。 

扫码关注团队公众号，了解更多团队动态、招聘信息和技术干货。

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？ 答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。

▽ 点击 | 阅读原文 | 获取最新论文推荐