条件随机场 (CRF 入门)—

条件随机场 (CRF 入门)——引言

条件随机场（CRF）这东西，第一次接触的时候，许多小伙伴恐怕都是一脸懵逼的。为啥？定义太多，形式太多。还没开始呢，一打开参考书，铺面而来的全是各种公式以及高大上的名词：概率无向图模型，团，全局马尔科夫性……

打住！我为啥要浪费生命学这破玩意？搞这个复杂的东西有什么用，能长出庄稼来吗？看看隔壁的SVM，随机森林，定义使用多么简单清晰，关键还厉害，深度学习出来前，那俩的分类准确度可是碾压其余一切的。

于是CRF就被残忍的抛弃了。

CRF：(○´･д･)ﾉ其实，人家比那俩更简单好学呢QAQ。

机器学习中确实存在一些拍拍脑袋想出来的模型，你若是探究它的原理，总会感觉作者在强词夺理。

但CRF的从诞生到实现，脉络都非常清晰，简明和合理才是它应有的标签。

人们在生活中，总能不自觉地发现事物之间的相关性，“天上钩钩云，地上雨淋淋”，“朝霞不出门，晚霞行千里”，“雄鸡报晓天下白”，“以史为镜，可以知兴替”，“初九，潜龙勿用”……

这些相关性本身并没有什么用，只是当人们使用这些相关性进行推断时，便拥有了预测未来的能力。

但并不是所有的相关性都是一因一果，简单直接的。一因多果，一果多因，互为因果，各种不同的形式层出不同。

为了更清晰地表达各种事物之间的关系，我们以事物为结点，以关系为边，做出了一张图，是为概率图模型。

于是一切关联，一目了然。但是图中结点纷扰繁多，推理不易。纵使是两个看似完全无关的事件，也可能经过多个相关事件周转后拥有了联系。

不能求解的模型，没有任何价值，为了更简便地应用其中的知识进行推断，我们对模型进行了简化，或者说添加了约束。

两个事件相关，不再是存在联通二者的路径，而是存在联通二者的，没有确定事件的路径。

换句话说就是：

1）当其他所有的事件确定了之后，两个没有边相连的结点，完全独立——成对马尔科夫性

2）当与某个事件直接相关的所有事件确定了之后，那个事件就与其他事件失去关联——局部马尔科夫性

3）如果将两个事件联系起来的所有事件都确定了，那么这两个事件无关——全局马尔科夫性

满足这上面三条性质中的任意一条，另外两条也会同时满足，这样的概率图无向图模型，也就是著名的马尔科夫随机场（MRF）。

自然，我们若是拥有足够的样本，便可以对MMF的联合概率分布进行模拟，然后再凭借这一近似结果对未知的事件进行推断——生成式模型

不过到了具体的事件上，我们发现这样做既不经济，也不实惠。明明我们知识想知道在已知X的情况下Y是多少，为啥非得把所有的分布全部都求出来？——判别式模型

于是条件概率模型（CRF）应运而生。

其实分析到这里已经够了。在直接给出CRF的数学定义之前，我们就已经可以利用CRF模型解决实际生活中的问题了。

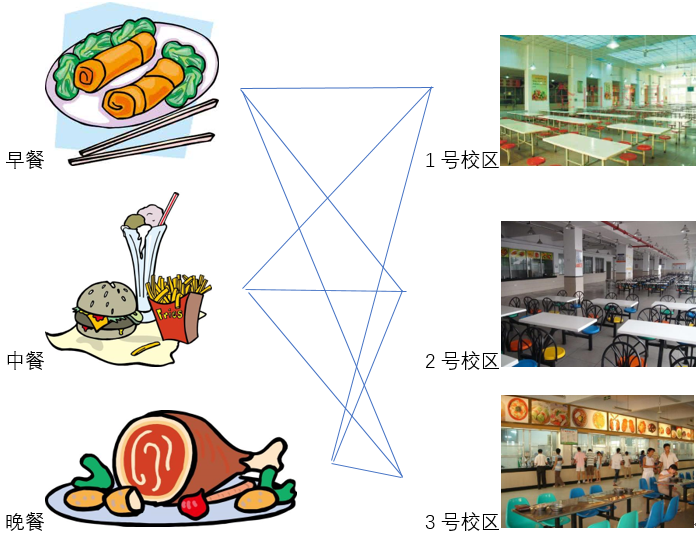
比如，小明一日三餐吃什么和他的位置有关，假如学校有123三个校区，相邻两餐的间隔时间只够他从一个校区转移到相邻的校区，而每个校区食堂的饭菜有相同也有不同。

那么，只要我们能够拥有大量的小明三餐吃的啥以及在哪吃的数据，不仅可以推断出每个校区的菜单以及小明对各道菜的评价，还可以根据小明一天的行动轨迹，推断他今天一日三餐最有可能吃了啥——这些都是简单的统计概率推断。

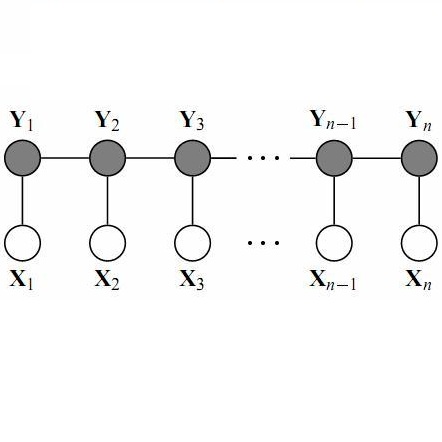
或者是根据一日三餐吃了啥来推断他今天的行动轨迹——这一推断过程就运用了CRF，在已知三餐食谱的条件下，每个时间点的位置仅仅与上一餐的位置有关（马尔可夫性）。因此我们可以以上一餐的位置，这一餐的位置，这一餐的食谱为变量，对这一餐的状态进行枚举，然后可以用Viterbi算法求解。

顺带一提，如果我们得到的训练数据中没有小明的用餐地点，那么这个模型就是隐马尔可夫模型（HMM）。我们一样可以生成每个校区的食谱，只是这模型的准确度就远不如CRF了。

当然，这只是一个简单的例子，目的只是为了方便理解，想要真正准确地弄懂CRF，还是必须再回到CRF的数学定义上。相信看完后面的篇幅再回来看这个例子，心中会有更深的理解。

《统计学习方法》李航

展开全文