仿人双足机器人步态规划-线性倒立摆(LIP)及其内在不稳定性
- 什么是LIP
近似化是处理复杂系统的一种有效方法。在天体力学中,尽管太阳和地球等行星有其复杂的内部结构,研究人员将它们简单近似为点质量而精确地算出它们在太阳系中的运行轨道。热力学中, 10^{23} 数量级的巨大分子群的运动状态经过近似化后,可以用温度和熵等几个参数来有效地描述和测量热力学现象。同样,为了抽象出双足运动的“本质”,对由几千个机械零部件和电子元器件构成的具有30个自由度的仿人机器人进行近似化时,我们作三个假设。第一,假定机器人的所有质量集中于其质心位置;第二,假设机器人的腿无质量,它与地面的接触是通过一个可以转动的支点实现的;第三,我们只考虑机器人的前后和上下方向的运动而忽略左右(横向)运动。换句话说,我们假定机器人的运动局限于由铅垂轴和步行方向的纵向轴所决定的二维平面内。在这些假定条件下,机器人可以简化为一个二维倒立摆( inverted pendulum)模型。

其动力学方程为
\ddot{x}_{\mathrm{c}}=\frac{g}{h_{o}}\left(x_{\mathrm{c}}-x_{\mathrm{a}}\right)+\frac{1}{m h_{o}}\left(\tau_{a}-\tau_{h}\right)+\frac{F(t)}{m}
- Point foot.
在没有扭矩的情况下,摆锤表示为无质量的伸缩腿,其脚位置为xa,且点质量m保持在恒定高度ho。 如果不采取任何措施,压力中心(CoP)将固定为xa。 在这种情况下,xa可被视为控制输入,并且在没有外部干扰的情况下,我们有
\ddot{x}_{\mathrm{c}}=\omega_{o}^{2} x_{\mathrm{c}}-\omega_{o}^{2} x_{\mathrm{a}}
其中: \omega_{o}=\sqrt{g / h_{o}}
此时,脚位置点就是ZMP。 x_{c o p}=x_{z m p}=x_a
关于ZMP,参见
- Finite-sized foot.
若踝关节力矩 \tau_{a} 存在,支撑点变为有限支撑面,则
x_{c o p}=x_{a}-\tau_{a} /(m g)
\ddot{x}_{\mathrm{c}}=\omega_{o}^{2} x_{\mathrm{c}}-\omega_{o}^{2} x_{c o p}
- Reaction mass.
质心会受到来自躯干运动的反作用力矩 \tau_{h} ,则
x_{c m p}=x_{c o p}+\frac{\tau_{h}}{m g}=x_{a}-\frac{\tau_{a}-\tau_{h}}{m g}
\ddot{x}_{\mathrm{c}}=\omega_{o}^{2} x_{\mathrm{c}}-\omega_{o}^{2} x_{c m p}
x_{c m p} 可视为外部作用的总和,我们用z(t)代指,得
\ddot{x}_{\mathrm{c}}(t)=\omega_{o}^{2} x_{\mathrm{c}}(t)-\omega_{o}^{2} z(t)
2. LIP的内在不稳定性
将LIP方程写成状态空间形式, \left(x_{\mathrm{c}}, \dot{x}_{\mathrm{c}}\right) 为状态量,z(t)为输入
\mathcal{S}_{c}:\left(\begin{array}{c}{x_{\mathrm{c}}} \\ {\dot{x}_{\mathrm{c}}}\end{array}\right) \quad A_{c}=\left(\begin{array}{cc}{0} & {1} \\ {\omega_{o}^{2}} & {0}\end{array}\right) \quad B_{c}=\left(\begin{array}{c}{0} \\ {-\omega_{o}^{2}}\end{array}\right)
进行坐标变换
\left(\begin{array}{c}{x_{\mathrm{u}}} \\ {x_{\mathrm{s}}}\end{array}\right)=\left(\begin{array}{cc}{1} & {1 / \omega_{o}} \\ {1} & {-1 / \omega_{o}}\end{array}\right)\left(\begin{array}{c}{x_{\mathrm{c}}} \\ {\dot{x}_{\mathrm{c}}}\end{array}\right)
整理后我们可以得到两个独立的状态量
\begin{aligned} \dot{x}_{\mathrm{u}} &=\omega_{o} x_{\mathrm{u}}-\omega_{o} z \\ \dot{x}_{\mathrm{s}} &=-\omega_{o} x_{\mathrm{s}}+\omega_{o} z \end{aligned}
x_{\mathrm{u}} 的特征值大于0,不稳定。
3. LIP不稳定的另一种解释
对倒立摆方程拉氏变换得到:
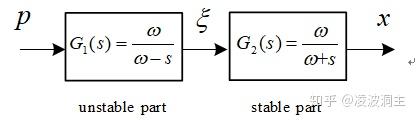
G(s)=\frac{\omega^{2}}{\omega^{2}-s^{2}}
G(s)=G_{1}(s) G_{2}(s)
其中: G_{1}(s)=\frac{\omega}{\omega-s}, \quad G_{2}(s)=\frac{\omega}{\omega+s}
4. 让不稳定分量有界的方法
- 一般情况
考虑系统:
\left[\begin{array}{c}{\dot{\gamma}_{+}} \\ {\dot{\gamma}_{-}}\end{array}\right]=\left[\begin{array}{cc}{\Lambda_{+}} & {0} \\ {0} & {-\Lambda_{-}}\end{array}\right]\left[\begin{array}{c}{\gamma_{+}} \\ {\gamma_{-}}\end{array}\right]+\left[\begin{array}{c}{L_{+}} \\ {L_{-}}\end{array}\right] \rho
\begin{aligned} \gamma_{+}(t) &=e^{\Lambda_{+} t} \gamma_{+}(0)+\int_{0}^{t} e^{\Lambda_{+}(t-\tau)} L_{+} \rho(\tau) d \tau \\ &=e^{\Lambda_{+} t}\left(\gamma_{+}(0)+\int_{0}^{t} e^{-\Lambda_{+} \tau} L_{+} \rho(\tau) d \tau\right) \end{aligned}
当:
\gamma_{+}(0)=-\int_{0}^{\infty} e^{-\Lambda_{+} \tau} L_{+} \rho(\tau) d \tau 时( \rho 有界时可保证该积分存在)
\begin{aligned} \gamma_{+}(t) &=-\int_{t}^{\infty} e^{\Lambda_{+}(t-\tau)} L_{+} \rho(\tau) d \tau \\ &=-\int_{0}^{\infty} e^{-\Lambda_{+} s} L_{+} \rho(t+s) d s \end{aligned}
该广义积分有界:
\left\|\gamma_{+}(t)\right\| \leq \frac{M}{\sigma_{+}}\left\|L_{+}\right\|\|\rho\|_{L_{\infty}}
其中:
-\sigma_{+}=\max _{i} \operatorname{Re} \lambda_{i}\left(-\Lambda_{+}\right)
M>0
- 倒立摆情况
根据上面的推导
x_{\mathrm{u}}(t ; z)=e^{\omega_{o}\left(t-t_{0}\right)} x_{\mathrm{u}}\left(t_{0}\right)-\omega_{o} \int_{t_{0}}^{t} e^{\omega_{o}(t-\tau)} z(\tau) d \tau
当初始条件满足
x_{\mathrm{u}}\left(t_{0}\right)=x_{\mathrm{u}}^{\star}\left(t_{0} ; z\right) \triangleq \omega_{o} \int_{t_{0}}^{\infty} e^{-\omega_{o}\left(\tau-t_{0}\right)} z(\tau) d \tau 时
x_{\mathrm{u}}^{\star}(t ; z)=\omega_{o} \int_{0}^{\infty} e^{-\omega_{o} \tau} z(\tau+t) d \tau
该结果有界,可保证LIP稳定,所以该初始条件可以作为QP的约束保证倒立摆稳定。
参考资料:
① Lanari, L., Hutchinson, S., & Marchionni, L. (2015). Boundedness issues in planning of locomotion trajectories for biped robots. IEEE-RAS International Conference on Humanoid Robots, 2015-Febru, 951–958.
② Lanari, L., & Wen, J. T. (1991). Feedforward calculation in tracking control of flexible robots. Proceedings of the IEEE Conference on Decision and Control, 2, 1403–1408.
③ 仿人机器人/【日】梶田秀司编著;管贻生译。一北京:清华大学出版社,2007.3


