Metric Learning科普文
度量学习(Metric Learning)是机器学习里面的一个研究方向,主要是用来学习一个距离或者用来降维,比如PCA、NCA等等都属于度量学习算法。
本文参考《A Tutorial on Distance Metric Learning: Mathematical Foundations, Algorithms and Software》这篇文章(92页),主要是介绍了一下距离度量学习(DML)里面涉及到的数学知识、距离度量学习的算法和工具包。

下面就按照文章的章节目录来介绍。
A 数学背景
机器学习里面经常会用到一些优化、矩阵和信息论的知识,在DML中也是。
- 优化
一些优化的基础知识,比如优化的定义、凸优化的定义等等,这里不重复,只补充几点:梯度下降(Gradient Descent)、凸投影(Convex Projection)、投影梯度下降(Projected Gradient Descent)、迭代投影(Iterated Projections)。
首先,回顾一下无约束优化问题:
\min_x f(x) \\
常用的解决方法是梯度下降,即:
x_{t+1} = x_t - \eta \nabla f(x_t) \\
其中 v_t = -\nabla f(x_t) 是负梯度方向,也是最速下降的梯度方向。这里解释一下为什么会是这样,采用一阶泰勒展开:
f(x + \delta) = f(x) + \delta \nabla f(x) + o(\delta) \\
取 \delta = -\eta \nabla f(x) 得到:
f(x - \eta \nabla f(x)) = f(x) - \eta \Vert \nabla f(x) \Vert^2 + o(\eta) \\
其中 o(\eta) 是泰勒展开式的余项,由于 \lim_{\eta \rightarrow 0} \frac{o(\eta)}{\eta} = 0 ,因此存在 0 < \eta^{*} < \epsilon ,使得:
\frac{o(\eta^{*})}{\eta^{*}} <\Vert \nabla f(x) \Vert^2 \\
因此,存在 \eta^{*} :
f(x - \eta^{*} \nabla f(x)) = f(x) + \eta^{*} \left( -\Vert \nabla f(x) \Vert^2 + \frac{o(\eta^{*})}{\eta^{*}} \right) \leq f(x) \\
因此,目标函数是下降的,参数更新为: x_{t+1} = x_t - \eta^{*} \nabla f(x_t) 。参数更新量记作 v_t = -\eta^{*} \nabla f(x_t) 。
实际上,只要满足 \langle v, \nabla f(x) \rangle < 0 即可实现目标函数的下降,而当 v = -\eta \nabla f(x) 时是梯度负方向,会使得目标函数下降最快,因此称为最速梯度下降。
然而有很多问题是有约束的,这里我们假设约束是凸的,因此我们使用梯度下降可能会得到一个不可行解,然后我们就将这个梯度方向再投影到可行区域,比如下图示例(橙色椭圆是优化目标,蓝色椭圆是约束可行域,红色是梯度下降更新方向,蓝色是投影梯度下降更新方向):

那么我们的优化问题变为:
\min_x f(x) \quad s.t. \quad x \in \mathcal{C} \\
其中 \mathcal{C} 是凸约束,那么投影梯度下降的方法为:
x_{t+1} = P_{\mathcal{C}}(x_t - \eta \nabla f(x_t)) \\
其中 P_{\mathcal{C}} 是一个映射,将一个向量映射到目标可行域,其定义为:
P_{\mathcal{C}}(x) = \arg\inf_y \{ d(x, y) : y \in \mathcal{C} \} \\
并且根据投影定理(Projection Theorem)有:
\langle x - P_{\mathcal{C}}(x), y - P_{\mathcal{C}}(x)\rangle \leq 0, \quad \forall y \in \mathcal{C} \\
比如下面的图示:
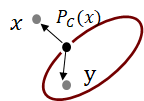
那么根据PGD的更新公式 x_{t+1} = P_{\mathcal{C}}(x_t - \eta \nabla f(x_t)) ,有 v_t = x_{t+1} - x_t = P_{\mathcal{C}}(x_t - \eta \nabla f(x_t)) - x_t ,即:
v = P_{\mathcal{C}}(x - \eta \nabla f(x)) - x \\
那么下面就说明 \langle v, \nabla f(x) \rangle \leq 0 。首先,如果 x - \eta \nabla f(x) \in \mathcal{C} ,那么显然有 v = -\eta \nabla f(x) ,和梯度下降一样;当 x - \eta \nabla f(x) \notin \mathcal{C} ,那么根据投影定理以及 x\in \mathcal{C} ,有:
\langle x - \eta \nabla f(x) - P_{\mathcal{C}}(x - \eta \nabla f(x)), x - P_{\mathcal{C}}(x - \eta f(x)) \rangle \leq 0 \\
即有:
\langle -v-\eta \nabla f(x), v\rangle \leq 0 \quad \Rightarrow \quad \langle v, \nabla f(x) \rangle \leq 0 \\
在度量学习里面,经常会涉及到带有约束的求解问题,因此需要配合使用投影梯度下降来求解。
- 矩阵分析
在数学背景知识里面,另外一块重要的则是矩阵分析。这里面会包括矩阵F范数(Matrix Frobenius norm)、半正定矩阵(Positive Semi Definite Matrix)、矩阵优化(Matrix Optimization)等知识。
首先是矩阵的F范数(F-内积),这里简单带过去,有以下定义和性质:
\langle A, B \rangle_F = \text{tr}(A^TB) = \sum_{ij}A_{ij}B_{ij} \\ \Vert A \Vert_F = \sqrt{\text{tr}(A^TA)} \\
性质有以下几点:
\Vert A \Vert_F = \Vert A^T \Vert_F \\ \Vert A U \Vert_F = \Vert V A \Vert_F = \Vert V A U\Vert_F, \quad V \in O_{d^{\prime}}(\mathcal{R}),\quad U \in O_d(\mathcal{R})
其中 O_d(\mathcal{R}) 表示 d\times d 的正交矩阵。
下面介绍一个关于如何把一个矩阵变为半正定矩阵的定理:
Let A \in S_d(\mathcal{R}) and have the spectral decomposition A = UDU^T , and the positive part A^{+} = UD^{+}U^T is the projection onto the positive semidefinite cone, where D^{+} = \text{diag}(\sigma_1^{+}, \sigma_2^{+}, \cdots, \sigma_d^{+}),\quad \sigma_i^{+} = \max(\sigma_i, 0).
Let A \in M_d(\mathcal{R}) , then ((A + A^{T})/2)^{+} is the projection onto the PSD cone.
也就是说,对于对称矩阵(用 S_d(\mathcal{R})表示 ),我们先做谱分解,然后将其负的奇异值变为0,那么得到的矩阵将是到半正定矩阵可行域的投影;对于非对称矩阵,先将其和对称矩阵相加得到的结果平均即可得到一个对称矩阵。详细的证明这里省略。
最后再介绍一下矩阵优化的东西,我们经常会遇到以下优化问题:
\max_{L \in M_{d^{\prime}\times d}} \text{tr}(LAL^T) \\ s.t. \quad LL^T = I
那么此时的最优化问题的解是对矩阵 A \in S_d(\mathcal{R}) 做特征值分解,取前 d^{\prime} 个最大特征值对应的特征向量组成的矩阵,即是最优解 L^{*} 。
- 信息论
下面介绍一下信息论(Information Theory)。首先是KL Divergence,又称为Relative Entropy的非负性:
KL(p||q) = E_{x\sim p(x)}\left[\log \frac{p(x)}{q(x)} \right] = E_{x\sim p(x)}\left[ -\log \frac{q(x)}{p(x)}\right] \geq -\log \int p(x)\frac{q(x)}{p(x)}dx = 0 \\
然而KL不是对称的,因此有Jeffery Divergence:
J(p||q) = KL(p||q) + KL(q||p) = \int_{-\infty}^{\infty}(p(x) - q(x))\log\frac{p(x)}{q(x)} dx \\
下面再引出Bregman Divergence,衡量两个矩阵变量的距离,其中 \phi : M_d(\mathcal{R}) \rightarrow \mathcal{R} 是一个凸函数,根据凸函数的性质,下面式子是非负的:
D_{\phi}(A||B) = \phi(A) - \phi(B) - \langle \nabla \phi(B), A - B\rangle_F \\\\
比如我们可以取:
\phi(X) = -\log \det(X) , \quad X \in S_d(\mathcal{R})^{+}\\
那么可以得到Log-Det Divergence(其中有 \nabla \phi(X) = -X^{-1} ):
D_{\phi}(A||B) = \log \det(B) - \log \det(A) + \text{tr}(B^{-1}(A-B)) = \text{tr}(AB^{-1}) - \log\det(AB^{-1}) - d \\
下面假设我们有两个高斯分布 p_1(x|\mu_1, \Sigma_1), p_2(x|\mu_2,\Sigma_2) ,那么我们有KL和Jeffery Divergence:
KL(p_1 || p_2) = \frac{1}{2}D_{\phi}(\Sigma_1 || \Sigma_2) + \frac{1}{2}\Vert \mu_1 - \mu_2 \Vert_{\Sigma_1^{-1}}^2 \\
Jeffery Divergence为:
J(p_1 || p_2) = \frac{1}{2}\text{tr}(\Sigma_1 \Sigma_2^{-1} + \Sigma_2\Sigma_1^{-1}) + \frac{1}{2}\Vert \mu_1 - \mu_2 \Vert_{\Sigma_1^{-1} + \Sigma_2^{-1}}^2 - d \\
本小节介绍了优化、矩阵、信息论相关的知识,尤其是以Projected Gradient Descent、Projection onto PSD cone、Log-Det Divergence为重点。
B. 度量学习算法
度量学习算法可以从降维(Dimensionality Reduction)、最近邻分类(Nearest Neighbors Classifier)、聚类中心(Cluster Centroids)、信息论(Information Theory)等角度进行归类。
首先介绍一下度量学习算法(Distance Metric Learning, DML)。先介绍一下马氏距离(Mahalanobis Distance),其形式为:
d_M(x, y) = \sqrt{(x-y)^TM(x-y)} = \langle x-y, x-y\rangle_M \\
其中 M \in S_d(\mathcal{R})^{+}_{0} 为半正定矩阵。一个好的度量矩阵会考虑各个特征之间的差别,比如下图的例子。其中绿色点是一类,都在同一水平线上,红色点是一类,也在同一水平线上,只不过分布稍微密集。左边是使用单位矩阵当作度量矩阵,相当于使用欧式距离对三个类别分类,由于横坐标量级比较大,因此学习到的分类界面并不理想;而合适的距离度量矩阵应该是右图显示的分类界面。

度量学习又可以理解为度量两个样本之间的相似度,适用于一些有约束的问题,比如以下约束:
S = \{(x_i, x_j) : x_i \text{ is similar to } x_j\} \\\\ D = \{(x_i, x_j) : x_i \text{ is not similar to } x_j\} \\\\ R = \{(x_i, x_j, x_k) : x_i \text{ is more similar to } x_j \text{ then } x_j\} \\
度量学习经常有两种解释,第一种就是上述方法学习一种度量矩阵 M \in S_d(\mathcal{R})^{+}_{0} ,优化以下问题:
\min_{M \in S_d(\mathcal{R})^{+}_{0}} l(d_M, S, D, R) \\
第二种是根据矩阵分解 M = L^TL, L \in M_{d^{\prime} \times d} 得到:
d_L(x, y) = \sqrt{(x-y)^TL^TL(x-y)} = \Vert L(x-y) \Vert_2 \\
那么得到的优化目标为:
\min_{L \in M_{d^{\prime}\times d}(\mathcal{R})} l(d_L, S, D, R) \\
一般来说,第一种因为其表达式 d_M = \langle M, (x-y)(x-y)^T\rangle_F 是线性的,因此绝大多数情况下都是Convex的,所以优化目标/约束都经常是凸的,即凸优化,有很多算法可以达到最优解;而 d_L = \Vert L(x-y) \Vert_2 则是二次项,如果前面有负系数出现在目标/约束里面则会导致问题非凸,因此只能求得局部最优解。
另外,使用 d_M 不方便引入一些约束,比如矩阵的秩, M \in S_d(\mathcal{R})^{+}_{0} 可以是低秩矩阵,但是一般来说秩的约束不是凸约束,所以施加了这个约束之后整个问题就非凸了,并且变得复杂了;此时需要使用 d_L ,因为限定 d^{\prime} < d 就可以达到低秩的要求。
这里解释一下秩的约束为什么不是凸的,比如现在约束秩是1,有两个矩阵 A = [[1, 0]; [0, 0]], B = [[0, 0]; [0, 1]] ,那么 (A + B) / 2 的秩就会变为2,不再是1。
下面就正式开始介绍度量学习算法。
- Dimensionality Reduction Based
基于降维的度量学习算法是学习一个到低维的映射矩阵,使得映射后的样本具有某些性质。包括无监督的PCA、有监督的LDA和ANMM。
- PCA & LDA
这两个算法就不多介绍了,PCA的优化目标是:
\max_{L \in M_{d^{\prime}\times d}} \text{tr}(L\Sigma L^T) \\ s.t. \qquad LL^T = I
LDA的优化目标是:
\max_{L \in M_{d^{\prime}\times d}} \text{tr}((LS_wL^T)^{-1}(LS_bL^T)) \\
其中 :S_w = \sum_c \sum_{i \in C_c} (x_i - \mu_c)(x_i - \mu_c)^T \\ S_b = \sum_c N_c(\mu_c - \mu)(\mu_c - \mu)^T\\
这里主要说一下两个算法的缺点,PCA是无监督的,不使用类别信息,最大化的是投影之后数据点的方差,所以对于下面的情况处理不了,黄色线是PCA的投影面;而LDA是使用了类别信息的,最大化类间距离,最小化类内距离,因此可以很好地选择绿色这个投影面。
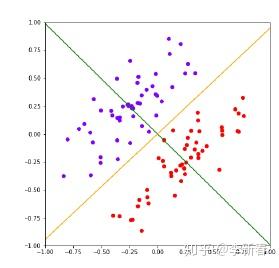
PCA和LDA的最优解分别是对 \Sigma 和 S_w^{-1}S_b 做特征值分解得到的,因此在LDA中, S_w^{-1}S_b 的特性就决定了最优解的性质。第一,如果LDA中,每个类别的样本数目很少,远小于样本特征维度,那么得到的 S_w 很有可能不是满秩的,因此不可逆;第二,由于有 \sum_c N_c (\mu_c - \mu) = 0 的约束,如果数据有 C 个类,那么矩阵 S_b 的秩最多为 C - 1,因此得到的特征值分解的成分最多为 C - 1,即最终低维空间的维度最多为 C - 1。
- ANMM
Average Neighborhood Margin Maximization可以很好地解决LDA的问题,首先定义几个概念:
\mathcal{N}_{i}^o 是 \xi-\text{nearest homogeneous neighborhood},是指的和 x_i 所属同一类别最近的 \xi 个样本; \mathcal{N}_{i}^{e} 是 \zeta-\text{nearest heterogeneous neighborhood},是指的不同类别的最近的 \zeta 个样本。
对于 x_i 来说,Average Neighborhood Margin指的是:
\gamma_i = \frac{1}{|\mathcal{N}_i^e|}\sum_{x_k \in \mathcal{N}_i^e}\Vert x_k - x_i\Vert^2 - \frac{1}{|\mathcal{N}_i^o|}\sum_{x_j \in \mathcal{N}_i^o}\Vert x_j - x_i\Vert^2 \\
假设我们使用了映射矩阵 L ,那么得到如下的优化目标:
\max_{L \in M_{d^\prime \times d}} \sum_{i=1}^N \left( \frac{1}{|\mathcal{N}_i^e|}\sum_{x_k \in \mathcal{N}_i^e}\Vert Lx_k - Lx_i\Vert^2 - \frac{1}{|\mathcal{N}_i^o|}\sum_{x_j \in \mathcal{N}_i^o}\Vert Lx_j - Lx_i\Vert^2 \right)\\\\
化简整理,记 S = \frac{1}{|\mathcal{N}_{i}^e|}\sum_i \sum_{x_k \in \mathcal{N}_{i}^e} (x_k - x_i)(x_k-x_i)^T , C = \frac{1}{|\mathcal{N}_{i}^o|}\sum_i \sum_{x_k \in \mathcal{N}_{i}^o} (x_k - x_i)(x_k-x_i)^T ,那么最后优化目标为:
\max_{L \in M_{d^\prime \times d}} \text{tr}(L(S-C)L^T) \\ s.t. \qquad LL^T = I
这么看的话ANMM不需要求逆矩阵,也没有类别数目限制矩阵的秩,解决了LDA的两个问题。
2. Nearest Neighbors Classifier Based
下面介绍一下基于最近邻的几个算法,包括LMNN和NCA,都是非常著名的距离度量学习算法。
- LMNN
LMNN全称是Large Margin Nearest Neighbors,目的是学习一种低维映射使得基于K-近邻的算法性能最好。
首先还是介绍两个概念,一个是target neighbors,一个是imposter。对于样本 x_i ,选择同类别最近的 k 个样本,这些样本被称为 x_i 的target neighbors,若 x_j 是其中一个target neighbor,那么用 j \rightarrow i 表示;如果此时存在一个不同类别的样本 x_l 满足 \Vert x_i - x_l \Vert^2 \leq \Vert x_i - x_j \Vert^2 + 1 ,那么称这个样本为 x_i, x_j 的imposter。
LMNN这个算法包括两种作用力,分别是pull和push。首先介绍pull,目的是将target neighbors拉的更近:
\epsilon_{pull} = \sum_{i} \sum_{j \rightarrow i} \Vert L(x_j - x_i) \Vert^2 \\
而push则相应地将imposter推地更远:
\epsilon_{push} = \sum_i \sum_{j \rightarrow i} \sum_l (1 - y_{il})\left[1 + \Vert L(x_i - x_j)\Vert^2 - \Vert L(x_i - x_l) \Vert^2 \right]_+ \\
对于push解释一下,肯定是先遍历所有的target neighbors对 x_i, x_j ,如果 x_l 和 x_i 属于同一类别,那么不计入损失;否则,观察这个样本是否是imposter,如果不是则不计入损失,否则计入损失,这个过程通过算子 []_+ 来实现。
那么最终的损失包括两部分加权得到:
\epsilon(L) = (1-\mu)\epsilon(pull) + \mu \epsilon(push) \\
当然也可以将 d_L 用 d_M 替换得到:
\epsilon(M) = (1-\mu)\sum_{i} \sum_{j \rightarrow i} \Vert x_j - x_i \Vert_M^2 \\ + \mu \sum_i \sum_{j \rightarrow i} \sum_l (1 - y_{il})\left[1 + \Vert x_i - x_j\Vert_M^2 - \Vert x_i - x_l \Vert_M^2 \right]_+
此时问题变成了一个凸优化问题,求解的话可以使用次梯度下降(Subgradient descent)和投影到半正定矩阵空间的方法来实现。
次梯度为:
G = (1-\mu)\sum_i \sum_{j \rightarrow i}O_{ij} + \mu \sum_{i,j,l\in\text{imposters}}(O_{ij} - O_{il}), \\ O_{ij} = (x_i -x_j)(x_i-x_j)^T
放一张示例图:

- NCA
NCA是Neighborhood Component Analysis的缩写,关于这个的介绍可以参考之前的一篇文章《https://zhuanlan.zhihu.com/p/48371593》。
这里简单介绍一下,NCA是基于最近邻分类的思想,目的是最大化最近邻分类的准确率。以第 i 个样本为中心,第 j 个样本的分布为:

这里引入马氏矩阵之后有:
p_{ij} = \frac{\exp\left( -\Vert Lx_i - Lx_j \Vert^2\right)}{\sum_{k\neq i}\exp\left( -\Vert Lx_i - Lx_k \Vert^2\right)}, \quad p_{ii}=0 \\
那么优化目标为:
\max_{L \in M_{d^\prime \times d}} \sum_i \sum_{j \in C_i} p_{ij} \\
3. Centroids Based
下面介绍一下基于Centroids的距离度量算法,即通过类中心进行分类的算法,而不是基于最近邻。
- NCMML
Nearest Class Mean Metric Learning,顾名思义,就是利用类别中心进行分类的度量学习算法。
首先给定一批数据 \{ (x_i, y_i)\}_{i=1}^N ,计算每个类别的中心记作 \mu_c = \frac{1}{N_c}\sum_{i:y_i=c}x_i ,然后样本 x 是第 c 类的概率为:
p_L(c|x) = \frac{\exp\left( -\frac{1}{2}\Vert L(x - \mu_c) \Vert^2 \right)}{\sum_{c^\prime} \exp\left( -\Vert L(x - \mu_{c^\prime}) \Vert^2 \right)} \\
那么NCMML最大化的就是条件分布的似然:
\mathcal{L}(L) = \frac{1}{N}\sum_{i=1}^N \log p_L(y_i | x_i) \\
使用梯度下降求解即可,梯度表达式为:
\nabla \mathcal{L}(L) = \frac{1}{N}\sum_{i=1}^N \sum_{c \in C}\alpha_{ic}L(\mu_c -x_i)(\mu_c-x_i)^T \\ \alpha_{ic} = p_L(c|x_i) - I[y_i=c]
4. Information Theory Based
基于信息论推导的一些距离度量学习算法,比如ITML和MCML等通常是使用距离度量矩阵定义一个分布,然后推导出最小化两个分布的KL距离或者Jeffery距离等等。
- ITML
ITML的全称是Information Theoretic Metric Learning。我们先看一下高斯分布和距离度量的关系:
p(x|\mu, \Sigma) = \frac{1}{(2\pi)^{d/2}\det(\Sigma)^{1/2}}\exp\left((x-\mu)^{T}\Sigma^{-1}(x-\mu) \right) \\
而马氏距离的定义为:
d^2_M(x, \mu) = (x -\mu)^TM(x-\mu) \\\\
注意,最准确的马氏距离的定义里面, M = \Sigma^{-1} 。因此可以说,给定一个 M ,我们可以得到一个马氏距离,同时也会得到一个高斯分布:
p(x|M) = \frac{1}{(2\pi)^{d/2}\det(M)^{1/2}}\exp\left((x-\mu)^{T}M^{-1}(x-\mu) \right)\\
那么,如果我们有一个先验 M_0 ,那么需要做的事情就是最小化两者之间分布的KL距离即可:
\min_{M \in S_d(\mathcal{R})^+} KL(p(x|M_0)||P(x|M)) \\ s.t. \quad d_M(x_i, x_j) \leq u, \quad (i,j) \in S \\ \qquad d_M(x_i, x_k) \geq v, \quad (i,j) \in D
并且,根据之前的两个高斯分布KL计算的结果可以得到Log-Det Divergence的表达式:
\min_{M \in S_d(\mathcal{R})^+} D_{ld}(M_0, M) \\ s.t. \quad d_M(x_i, x_j) \leq u, \quad (i,j) \in S \\ \qquad d_M(x_i, x_k) \geq v, \quad (i,j) \in D
后续算法会继续引入松弛变量等等,这里不再详细介绍。
- MCML
MCML的全称是Maximally Collapsing Metric Learning,也是有监督的学习算法。
MCML的原理更加简单了,首先定义 p_M(j|i) :
p_M(j|i) = \frac{\exp\left( -\Vert x_i - x_j\Vert_M^2\right)}{\sum_{k\neq i}\exp\left( -\Vert x_i - x_k\Vert_M^2\right)} \\
然后根据真实的 p_0(j|i) :
p_0(j|i) = I[y_i=y_j] \\\\
然后优化目标就是:
\min_{M \in S_d(\mathcal{R})_0^+} f(M) = \sum_{i=1}^NKL(p_0(\cdot|i)||p_M(\cdot||i)) \\
5. Other specific algorithms
- MMC
最后再介绍一个MMC,全称是Mahalanobis Metric for Clustering。主要思想非常简单,主要是下面的式子:
\min_M \sum_{(i,j) \in S} \Vert x_i - x_j\Vert_M^2 \\ s.t. \quad \sum_{(i,j) \in D} \Vert x_i - x_j\Vert_M^2 \geq 1 \\ \qquad M \in S_d(\mathcal{R})^{+}_0
最后总结一下本文介绍的几个度量学习算法,总结为下图:

C. 度量学习算法包
这里主要是介绍Python的算法包,第一个是metric-learn,包括NCA、ITML、LMNN、MMC等9种有监督度量学习算法,链接为:

其次就是这篇论文提出的pyDML,包括17种度量学习算法,包括本文介绍的所有算法,PCA、LDA、ANMM、LMNN、NCA、NCMML、ITML、MCML、MMC等,链接为:

D 深度度量学习
下面简单介绍一下深度度量学习:利用深度网络学习一个表示(Embedding),采用各种采样方法(Sampling),比如成对/三元组训练样本(Triplet),计算一个带有Margin/最近邻等分类或聚类算法的损失。
主要框架是下面的方法:

和浅层度量学习对比一下,提取特征生成Embedding的部分同等于Shallow DML里面的矩阵 L/M 的作用;然后通过Sampling选取一些样本对当作训练数据,即Shallow DML中的约束 S、D、R 等;最后计算Loss,损失的计算需要根据最近邻/Margin/信息论等设计。
关于深度度量学习的Embedding部分,无非就是设计很多网络结构,比如用CNN,LSTM或者AE来完成;在Sampling部分有Naive Sample, Semi-hard Sample, N pairs sample等等,常见的还是三元组Triplet;在Loss层面包括Contrastive Loss, Triplet Loss, Margin Based Loss等等。
关于DeepML的更多推荐读者阅读:
最后利用一张图总结一下度量学习的一些要素和名词:


