数据降维与聚类（一）：主成分分析Principal Component Analysis（PCA）

本文的主要目的是为有高数和线性代数基础的同学们进行一些机器学习数学理论的讲解，也算是对本人所学知识的一次自我检查。希望读者不要被大量的公式吓到，公式数量多的主要原因是我尽量把所有的推导过程和结论都写上，避免阅读时产生“这个公式从哪儿来的?”的疑惑。

假设现在有一组数据向量 \{\mathbf{y}_t\}_{t=1}^T ,每个向量 \mathbf{y}_t 的长度为 D\times1 。那么主成分分析的第一步就是找到一个 d 维度( d\ll D )的线性子空间 \mathcal{S} ，使 \{\mathbf{y}_t\}_{t=1}^T 和其在 \mathcal{S} 上的投影的正交分解距离最小，如下图所示：

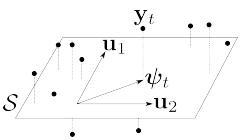
向量 \mathbf{y}_t 在 \mathcal{S} 上的投影 \mathbf{\psi}_t ，长度为 d\times1 ,可以看作是“压缩后”的d维数据。通过选择 d 的数值，我们可以在 \mathcal{S} 上很好的估计出原始数据。

现在假设有一个大小为 D\times T 的数据矩阵 \mathbf{Y} ，由 T 个向量 \mathbf{y}_t 组成。为简化后续内容和，我们假设数据 \mathbf{Y} 已经被中心化，即 \sum_{t}\mathbf{y}_t = \mathbf0 。如果原始数据没有中心化，则可以用 \mathbf{y}_t-\bar{\mathbf{y}} 的方式进行处理，其中 \bar{\mathbf{y}} 为数据的平均值 （1/T）\sum_{t}\mathbf{y}_t 。对于 d 维线性子空间 \mathcal{S} ,可以被等价表示为一组包含 d 个向量的正交基 \{\mathbf{u}_i\}_{i=1}^d 。那么，将 \mathbf{y}_t 映射到 \mathcal{S} 上的过程可以表示为 \sum_{i=1}^d(\mathbf{y_t^\top}\mathbf{u}_i)\mathbf{u}_i = \mathbf{U} \mathbf{U}^\top\mathbf{y_t} ,其中 \mathbf{U} =[\mathbf{u}_1,\mathbf{u}_2,\dots,\mathbf{u}_d] .根据上述的分析，我们可以定义数据 \mathbf{Y} 在 \mathcal{S} 上的第 i 个“成分“（component）为：

\mathbf{c}_i :=[\mathbf{y}_1^\top\mathbf{u}_i,\mathbf{y}_2^\top\mathbf{u}_i,\dots,\mathbf{y}_T^\top\mathbf{u}_i]^\top = \mathbf{Y}^\top\mathbf{u}_i ;

注意由于数据 \mathbf{Y} 是中心化的，所以成分 \mathbf{c}_i 的样本均值为(1/T)\sum^{T}_{t=1}c_{it} =(1/T)\mathbf{c}_{i}^{\top}\mathbf{1}_{T}=(1/T)\mathbf{u}_{i}^{\top}\mathbf{Y}\mathbf{1}_{T}=0 ; 因此，主成分 \mathbf{c}_i 的方差为 Var(\mathbf{c}_i )= (1/t)||\mathbf{c}_i ||_2^2=(1/T)\mathbf{u}_i^{\top}\mathbf{Y}\mathbf{Y}^{\top}\mathbf{u}_i 。假设样本的协方差矩阵已知，即 \hat{\mathbf{C}}_{yy}:=(1/T)\sum_{t=1}^{T}\mathbf{y}_t\mathbf{y}_t^{\top} = (1/T)\mathbf{Y}\mathbf{Y}^{\top} , 可以得到： Var(\mathbf{c}_i) =\mathbf{u}_i^{\top}\hat{\mathbf{C}}_{yy}\mathbf{u}_i 。由Courant-Fischer最小最大定理[1]可知, 能够最大化 Var(\mathbf{c}_i) 的向量 \mathbf{u}_i 即为 \hat{\mathbf{C}}_{yy} 的最大奇异值所对应的单位规范奇异向量。

总结一下，PCA的目的是：寻找 d 个主成分，即等价于构造一个正交矩阵 \mathbf{U}_d\in R^{D\times d} ，使其成为如下最大化问题的解：

max_{\mathbf{U_d}} trace(\mathbf{U}_d^{\top}\hat{\mathbf{C}}_{yy}\mathbf{U}_d) （1）

s.t. \mathbf{U}_d^{\top}\mathbf{U}_d = \mathbf{I}_d

根据Courant-Fischer最小最大定理 ，\mathbf{U}_d 的解即为 \hat{\mathbf{C}}_{yy} 的 d 个最大奇异值所对应的奇异向构成的矩阵。

另外一种PCA的解释方式[2]为，最小化如下数据重构问题的误差：

min_{\mathbf{U}_d}(\sum_{t=1}^{T}||\mathbf{y}_t-\mathbf{U}_d \mathbf{U}_d^{\top}\mathbf{y}_t||_2^2 = ||\mathbf{Y}-\mathbf{U}_d \mathbf{U}_d^{\top}\mathbf{Y}||_F^2) （2）

s.t. \mathbf{U}_d^{\top}\mathbf{U}_d = \mathbf{I}_d 。

上式的 ||\bullet||_F 为 Frobenius范数。（2）求出的 \mathbf{U}_d 与（1）式本质是相同的，证明如下：

||\mathbf{Y}-\mathbf{U}_d \mathbf{U}_d^{\top}\mathbf{Y}||_F^2= ||\mathbf{Y}||_F^2-2 trace(\mathbf{U}_d^{\top}\mathbf{Y}\mathbf{Y}^{\top}\mathbf{U}_d)\\+trace(\mathbf{Y}^{\top}\mathbf{U}_d\mathbf{U}_d^{\top}\mathbf{U}_d\mathbf{U}_d^{\top}\mathbf{Y}) \\=||\mathbf{Y}||_F^2-trace(\mathbf{U}_d^{\top}\mathbf{Y}\mathbf{Y}^{\top}\mathbf{U}_d)\\=||\mathbf{Y}||_F^2-T\cdot trace(\mathbf{U}_d^{\top}\hat{\mathbf{C}}_{yy}\mathbf{U}_d) 。

在文初我们提到，PCA要寻找数据 \mathbf{Y} 的"最优"线性子空间 \mathcal{S} 。那么基于L2范数最小误差的概念，PCA要解决的根本问题是：

min_{\mathbf{Z}\in R^{D\times T},\\rank(\mathbf{Z}\leq d)} ||\mathbf{Y}-\mathbf{Z}||_F^2 (3)

根据Schmidt-Eckart-Young-Mirsky定理[3], \mathbf{Z} 的解可由 \mathbf{Y} 的奇异值分解（SVD）求得。假设 \mathbf{Y} 的奇异值分解结果为,\mathbf{Y} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\top},其中 \mathbf{U}\in \mathbf{R}^{D\times D} , \mathbf{V}\in \mathbf{R}^{T\times T} 为奇异矩阵， \mathbf{\Sigma}的主对角线上的值为由大到小排列的奇异值；那么问题（3）的解即为 \mathbf{Z} = \mathbf{U}_d\mathbf{\Sigma}_d\mathbf{V}_d^{\top} ，即选择了 d 个最大奇异值及与其对应的奇异向量的积。

那么在第一张图中， PCA又是如何降维的呢？ \mathbf{\psi}_t 是 \mathbf{y}_t 在子空间 \mathcal{S} 上的投影，这个投影的过程可以表示为 \mathbf{\psi}_t = \mathbf{U}_d^{\top}\mathbf{y}_t ，其中 \mathbf{U}_d^{\top} 可以视作“压缩过程”，相应的， \mathbf{U}_d 可以视作“解压过程”，即 \mathbf{y}_t = \mathbf{U}_d \mathbf{\psi}_t 。既然存在 \mathbf{U}_d 这样的“完美”解压过程运算，那么存在非线性压缩运算 \mathbf{G}^{\top}\in R^{D\times d} , 且 \mathbf{G}^{\top} 的最优解即为 \mathbf{U}_d^{\top} ，如下式所述：

||\mathbf{Y} -\mathbf{U}_d\mathbf{U}_d^{\top}\mathbf{Y}||_F^2 = min_{U,G\in R^{D\times d};\\\mathbf{U}^{\top}\mathbf{U} = \mathbf{I}_d}\sum^{T}_{t=1}||\mathbf{y}_t-\mathbf{U}\mathbf{G}^{\top}\mathbf{y}_t||_2^2 。

最后，主成分分析的算法步骤总结如下：

输入：数据 \mathbf{Y} ：=[\mathbf{y}_1 ,...,\mathbf{y}_T]\in R^{D\times T}

1, 对 \mathbf{Y} 进行SVD： \mathbf{Y} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\top} ；

2，确定基向量：取 \mathbf{U} 中对应 前d个最大奇异值 的前d列构成新矩阵 \mathbf{U}_d ；

3，压缩训练数据：计算 \mathbf{\Psi}：=[\mathbf{\psi}_1,...,\mathbf{\psi}_T]:=\mathbf{U}_d^{\top}\mathbf{Y} ;

4， 重建估计训练数据： \hat{\mathbf{Y}}=\mathbf{U}_d\mathbf{\Psi} =\mathbf{U}_d\mathbf{U}_d^{\top}\mathbf{Y} ;

5，压缩实测数据：对任意 \mathbf{y}\in R^{D} ， 计算其压缩至 d 维后的数据： \mathbf{\psi}=\mathbf{U}_d^{\top}\mathbf{y} ;

6, 重建估计实测数据： \hat{\mathbf{y}}=\mathbf{U}_d\mathbf{\psi} =\mathbf{U}_d\mathbf{U}_d^{\top}\mathbf{y} 。

读者可按照具体需求截取部分或全部步骤进行主成分分析。

参考文献：

[1] Horn, Roger A., and Charles R. Johnson.Matrix analysis. Cambridge university press, 2012

[2]Pearson, Karl. "LIII. On lines and planes of closest fit to systems of points in space."The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science2.11 (1901): 559-572.

[3]Ben-Israel, Adi, and Thomas NE Greville.Generalized inverses: theory and applications. Vol. 15. Springer Science & Business Media, 2003.

最近还有一篇deadline要赶，后续还会更新其他主成分分析方法和降维运算的方法。这是我首次尝试在知乎写学术性的文章，还望各位读者多多指教，有不懂的地方也欢迎随时私信，回复看心情好坏而定，没错我就是这么皮。