图形演算和向上平面性 I
A. 向上平面性的理论基础
A.1 向上平面性的意义
向上平面画法(upward planar drawing)是定向图的一种平面画法,其特殊性在于要求每条定向边都是从下往上画的(或朝向任意一个固定方向),例见下图。
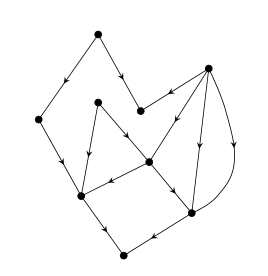
正如平面性是指平面画法的存在性,向上平面性则是指向上平面画法的存在性。
一个定向图如果有一个向上平面画法,则称为向上平面图(upward planar graph)。显然,向上平面图都是无环的(acyclic),因此都是因果网络(causal-network,或称无环定向图)。向上平面画法是因果网络的自然画法,向上平面性之于因果网络的意义正如平面性对于无向图的意义。
A.2 向上平面性的三个研究动机
任意有限偏序集都可以用一个唯一的因果网络表示(覆盖图,covering graph),因此可以用因果网络的向上平面性可以定义有限偏序集的平面性。 事实上,有限偏序集的平面性就是指覆盖图的向上平面性(具有平面哈斯图),它是发展向上平面图理论的最早动机。
另一个早期的研究动机来自于一个应用领域----理论计算机科学中的图形绘制(Graph Drawing)。向上平面画法主要用来表示一些等级结构(hierarchical structure),如项目管理中的PERT 网络(PERT=计划评估和审查技术),知识表示图中的ISA层级(ISA hierarchy),子程序调用图(subroutine call chart)等。
最近几年,在【4】中,我们为半群范畴(semigroupal category)的图形演算理论,2-范畴(2-category)的图形演算理论发展了一套组合框架,为它们建立了严格的数学基础,得到了权威专家的好评。它们都和向上平面性密切相关。 特别地,在【4】中,我们还证明了张量范畴(monoidal category)的图形演算理论和向上平面图理论的等价性,这一发现为两个理论的发展带来了新的动机,为它们建立严格的理论基础是本项目的第一个要完成的目标。
A.3 向上平面性的基本问题
向上平面性理论到现在虽然已经有几十年的历史,研究成果颇丰,但其理论基础仍不完善,有许多基本问题没有解决,甚至没有被提出来。本项目的主旨之一就是要彻底解决这些基本问题。
众所周知,平面性是图的一个基本拓扑性质,那么对于因果网络具有同等地位的向上平面性是否是一个拓扑性质呢?这是第一个基本问题(Q1),称为拓扑性问题。这一问题是整个领域最基本最困难的问题,在文献中还没有被明确地提出来。这个问题的本质是一个概念性问题,即确定向上平面画法等价性的正确定义,或者说在什么情况下我们才可以称两个向上平面画法等价的问题(详见后文分析)。
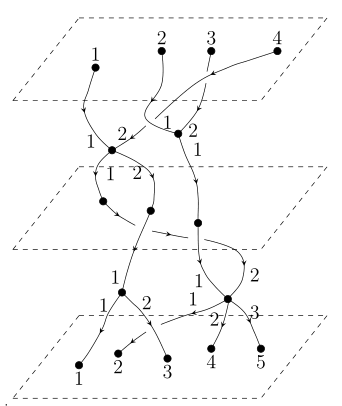
(Q1)之后,该领域的第二个基本问题(Q2)就是关于向上平面图等价类的一系列问题,包括等价类的刻画,判定算法,复杂性,标准型等问题,简称为等价类问题,其中等价类的组合刻画问题是最核心的,是我们研究的一个重点。在【5】中,我们提出了向上平面序(upward planar order)的概念(见下图),给出了向上平面性一个纯组合刻画。在向上平面序的框架下,我们将彻底解决等价类的组合刻画问题。

A.4 (Q1)和(Q2)的难点
(Q1)迟迟没被解决的原因在于它是一个隐藏很深的问题,其难点在于它既是一个概念性和语言的问题,又是一个原则性和正确动机的问题。下面我们从时间发展的角度来分析(Q1)的难点。
首先讨论在我们的工作【4】之前,即张量范畴的图形演算和向上平面性理论的等价性被发现之前,两个领域的理论困境:
(1)在向上平面图领域中,向上平面画法等价性的定义似乎应该和无向图的平面画法等价性的定义方式一样,即如果两个平面画法之间存在一个平面同痕,则称二者等价(定义1)。这看起来像是一个很自然的方案。按此定义,向上平面性和平面性一样,显然成为拓扑性质。但是,已经知道平面性和向上平面性的判定复杂性不一样,前者是P问题,后者是NPC问题【12】。所以,定义1并不像它看起来地那么自然。再者,为了强调平面性和向上平面性的区别,还有一个更自然的方案:如果两个向上平面画法可以向上平面同痕系起来,即在形变过程中保持每一个中间画法都是向上平面的,则称二者等价(定义2)。这一定义直观上和复杂性差异更加协调,但问题在于无法解决向上平面性的拓扑性问题。所以最理想的方案就是证明定义1和定义2是等价的,但事实上这是不可能的。例如下图中的两个向上平面画法,它们按照定义1是等价的,但是按照定义2则不等价。最近,在向上平面图的研究领域,【37】给出了向上平面图等价的一个新定义(定义3),并证明了定义3蕴含定义2,但是其工作并不能解决(Q1)。所以,(Q1)作为一个概念性问题,并不平凡,它也涉及到不同原则的选择。
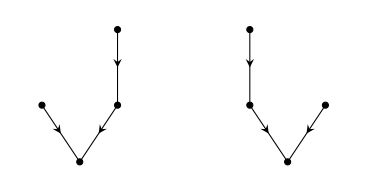
(2)在范畴论领域, Selinger在2011年提出了一个关于图形演算的拓扑性猜想【19】。这个猜想的原始表述显然是错误的,因为上面的例子就是反例,但是这个猜想仍然有意义,它指向的本质问题就是(Q1)。最近,Antonin和Jamie给Selinger的拓扑性猜想一个正面的回答(上面的例子就是他们提供的),在技术上解决了图形演算的拓扑性问题,但对于(Q1)仍然不够充分,还缺乏一个恰当的数学语言把他们的工作翻译为一个数学定理。所以,(Q1)不仅是概念性问题,更是一个涉及恰当语言问题。
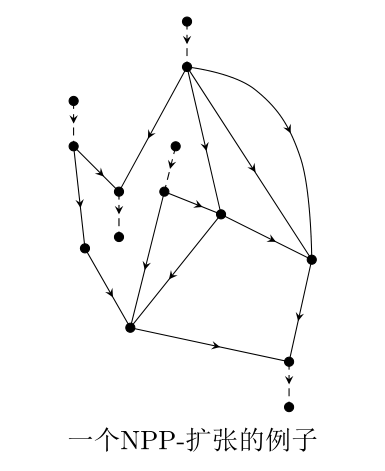
现在在解决了图形演算和向上平面性的统一性问题【4】之后,我们可以完美地解决(Q1)。第一,图形演算理论为向上平面画法等价的定义提供了正确的动机:根据图形演算理论,向上平面画法等价的定义应该取为定义2(由Joyal和Street给出),这个定义的正确性是由向上平面图的代数意义给出的。第二,对图形演算的unit convention和图形画法领域的bimodal嵌入的关系的认识帮助我们引入了一个关键概念----NPP-扩张(即对每一个source和sink加一个自由的叶子,见下图),借助这一本质的概念可以完美地解决Selinger猜想所面临的语言困境:每一个向上平面画法都有唯一的NPP-扩张,两个向上平面画法等价(关于定义2)当且仅当它们的NPP-扩张关于定义1是等价的。第三,类似于【5】中CPP-扩张,NPP-扩张的引入是自然的,也和图形演算的unit convention相关。在我们的工作【5】之前,向上平面性有两个基本的刻画,一是由Di Battista, Tamassia【8】和Kelly【9】独立给出的(刻画1,用平面st扩张),另一个是由Bertolazzi等人在【10,11】中给出(刻画2,用consistent large angle assignment,简称CLA-分派)。现在,我们用单位约定(unit convention)和NPP-扩张分别给出了刻画1和刻画2的完备代数解释。可见,(Q1)的完整解决需要两个领域的配合,一个提供概念和原则,一个提供语言和动机。

(Q2)的难点主要在组合方面。在【5】中我们提出了向上平面序的概念来刻画向上平面性,但是这个刻画并没有唯一性,即同一个向上平面画法在不同的形变下可以对应不同的向上平面序。因此,我们需要对向上平面序引入等价性的概念(见下图例子),使得向上平面序的等价类和向上平面画法的等价类一一对应,现在这一工作已经完成(见后文分析)。

A.5(Q1)和(Q2)的意义
在【4】中,我们证明了向上平面图理论和严格张量范畴的图形演算理论的等价性,因此(Q1)的解决将同时为两个理论建立一个统一坚实的数学基础。事实上,在证明两个理论的等价性之后,(Q2)将被翻译为张量范畴中的字问题。在【4】和【5】的基础上,(Q2)的解决不仅会为组合学贡献一个新的研究领域,而且将会极大地推动张量范畴理论和应用研究的发展。
A. 拓扑序论=高亏格向上平面性理论
B.1 拓扑序论的动机
发展拓扑序论有两个自然的动机(注2),其一来自向上平面性的研究,其二来自图形演算的研究。首先,关联结构和序结构是最基本且相似的组合结构,前者常用图来表示,后者则常用因果网络或偏序集表示。平面性是图的基本拓扑性质,对它的研究已经发展为图论中最经典,成熟的分支,即拓扑图论(topological graph theory)。相应的,序结构的基本拓扑性质是向上平面性(见上文中的(Q1)),对它的研究目前只限制在平面上。如何发展一个高亏格的向上平面性理论(Q3),即可以和拓扑图论等量齐观的拓扑序论(topological order theory)是一个很自然也很有意义的数学问题。这个问题由来已久,已经有一些尝试,但都不成功。其次,在【3】中,Joyal和Street为张量范畴的图形演算建立了一套拓扑理论;在前期工作【4】,【5】和部分未发表的工作中,我们发展了一个与之平行的组合理论。但是对于对称张量范畴的图形演算,Joyal和Street给出的是一个组合理论【3】,于是一个自然的问题就是:能不能反过来为对称张量范畴的图形演算找到一个平行的拓扑理论?由于我们已经知道严格张量范畴的图形演算理论等价于经典的向上平面性理论,并且对称张量范畴的图形演算自然地推广了严格张量范畴的图形演算,因此我们猜测:如果找到对称张量范畴背后的拓扑理论,那么它必然是经典向上平面性理论的自然推广,并且显然也是一个关于因果网络的拓扑理论。总之,两个方向的思考,都要求寻找一个关于序的拓扑理论,即拓扑序论。
B.2 建立拓扑序论的难点
平面图概念的自然推广是图在曲面上的嵌入,它是拓扑图论的主要研究对象。同样地,向上平面图的自然推广应该是因果网络在曲面上的向上嵌入(upward embedding),它应该是拓扑序论的主要研究对象。两个理论的对比见下图。显然,建立拓扑序论(Q3)的首要难点在于其主要研究对象的确立,即(1)给出因果网络在曲面上的向上嵌入的正确定义;(2)证明向上嵌入的拓扑性。只有完成了这两个工作,拓扑序论才能成为一个严格的数学理论。
在平面的情形,向上平面性的概念是建立在平面上的一个固定方向的,虽然不唯一,但所有的方向都等价。当考虑高亏格的情形的时候,固定方向的选择就成为问题。在【4】中,我们给向上平面性一个纯代数的解释,这比经典的几何定义更有优势,因为它可以自然地推广到高亏格(见下图)。事实上,我们发现对称张量范畴的图形演算可以看做严格张量范畴的图形演算的高亏格推广,而后者等价于经典的向上平面性理论,故对称张量范畴的图形演算为定义向上嵌入提供了一个自然的背景。至于向上嵌入的拓扑性,和平面情形类似(Q1),可以用同样的方法解决。
注1:我们这里的拓扑序论(topological order theory)和理论凝聚态物理中的拓扑序理论(theory of topological order,也称为theory of topological phase)虽然名字接近,但二者是不同的且独立的理论,一个是关于向上平面性的理论,一个是关于物质状态的理论。值得强调的是,在我们发展的因果凝聚理论中,二者又可以有机地统一起来,见后文分析。
注2:除了前两个明确的动机,还有第三个与迁移曲面(translation surface /very flat surface)【23】有关的动机。它以费米面上的电子散射为物理背景,其目标是把Kelly的关于向上平面图的直化定理【9,24】(相当于Fary直化定理的定向版本)推广到高亏格迁移曲面上去,其中每个定向边都是向上测地线/直线。不难理解,这个问题也和迁移曲面的多边形镶嵌有关,可能会推广Mohar等人的结果【25,26,27】。


B. 普适任意子模型和Joyal-Street拓扑场论
C.1 普适任意子模型和Joyal-Street拓扑场论的动机和意义
在【3】中,Joyal 和Street用3d boxed polarized and anchored progressive graph(简称3d boxed PAP-graph,例见下图)建立了辫子张量范畴图形演算的数学理论。这一理论和张量范畴,对称张量范畴的情形均不同:张量范畴的图形演算是用progressive plane graph描述的, 是一个纯拓扑的理论; 对称张量范畴的图形演算是用polarized and anchored progressive graph(简称PAP-graph)描述的,是一个纯组合的理论。
3d boxed PAP-graph是组合结构与拓扑结构相混合的概念,因为3d嵌入是拓扑概念, 而极化结构(polarization)和锚结构(anchor)则是组合概念。之前,我们已经给progressive plane graph找到了一个组合刻画,即upward planar order, 又为PAP-graph找到了一个拓扑描述,即因果网络在曲面上的向上嵌入,因此很自然地我们可以提出这样的问题(Q4):能不能为辫子张量范畴的图形演算找到一个纯组合的和一个纯拓扑的概念来描述? 这一问题的研究完全是我们前期研究的自然深化,也是我们的主要动机。
经过两三年的探索,我们已经看清了这一问题的前景,发现它与辫子张量范畴的字问题,拓扑量子场论,低维拓扑以及拓扑量子计算有密切联系。
首先,(Q4)可翻译为辫子张量范畴中的字的拓扑描述和组合描述的问题。
其次,它和拓扑量子场论有自然的联系:对于对称张量范畴的情形(即拓扑序论),它的第三个动机是描述费米面上的电子散射。而对于辫子张量范畴的情形,它的一个可能应用就是可以描述费米面上任意子的散射。这个现象的完整物理理论是陈-西蒙斯-威腾理论,这是一个著名的三维拓扑场论。根据维基百科上的提醒,这个理论仍有未解决的问题(如高亏格情形的量子化及分析,琼斯多项式的高亏格推广),且和虚纽结(virtual kont)理论有关。
我们摘抄如下(见https://en.wikipedia.org/wiki/Virtual_knot):
A reason why virtual knots are important, and a relation between QFT (quantum field theory) and virtual knots.
Virtual knot itself is a fascinating object. Virtual knots have many exciting connections with other fields of knots theory. One of the most important reason why we need virtual knots is as follows.
Problem(Extension of Jones polynomial to general 3-manifolds)
``The original Jones polynomial was defined for 1-links in the 3-sphere (the 3-ball, the 3-space R3). Can you define the Jones polynomial for 1-links in any 3-manifold?’’
See section 1.1 of this paper [KOS] [1] for the background and the history of this problem. Kauffman submitted a solution in the case of the product manifold of closed oriented surface and the closed interval, by introducing virtual 1-knots [2]. It is open in the other cases. Witten’s path integral for Jones polynomial is written for links in any compact 3-manifold formally, but the calculus is not done even in physics level in any case other than the 3-sphere (the 3-ball, the 3-space R3). This problem is also open in physics level. In the case of Alexander polynomial, this problem is solved.
这一信息提示我们(Q4)和虚链环理论(virtual link theory【6】)有关,而且据我们观察也应该和虚空间图论(virtual spacial graph theory【7】)有关。
第三,(Q4)和低维拓扑密切相关。一般地,人们都认为雷希蒂欣-图拉耶夫理论(Reshetikhin-Turaev theory)【22】是陈-西蒙斯-威腾拓扑场论的非微扰量子化,是一种代数版本的拓扑量子场论。该理论利用一种特殊的线性辫子张量范畴(modular tensor category)和三维流形的链环表示,给出了3为流形的拓扑量子不变量。我们注意到:(1)物理地来看,雷希蒂欣-图拉耶夫理论可以看做是加厚曲面上的拓扑场论;(2)3d boxed PAP-graph的组合部分(极化和锚结构)可以翻译为图在曲面上的向上嵌入,拓扑部分则和图在加厚曲面上的嵌入有关;(3)库珀伯格(Kuperberg,【30】)证明了虚链环的唯一表示定理:每一个虚链环可以唯一地表示为图在具有极小亏格的加厚曲面上的嵌入。基于这三个观察,我们猜测(Q4)应该和虚链环理论和雷希蒂欣-图拉耶夫理论密切相关。
第四,辫子张量范畴是一类非常普遍的数学结构,基于前面的分析,我们认为(Q4)的解决将会给出辫子张量范畴的图形演算和虚链环理论的自然统一。由于现在比较热门的拓扑量子计算可以很自然地使用辫子张量范畴的语言,而拓扑量子计算的主要物理载体就是任意子,因此我们把这个统一的组合理论命名为普适任意子模型。另外,我们相信(Q4)的解决也会定义一种新的更一般的3维拓扑场论,我们把得到的拓扑理论命名为Joyal-Street 拓扑场论,它将是雷希蒂欣-图拉耶夫理论的非线性推广(前者是在一般张量范畴的基础上定义的,而后者是在特殊的线性张量范畴,即模张量范畴的基础上定义的)。
C.2 建立普适任意子模型和Joyal-Street拓扑场论的难点
普适任意子模型的主要问题就是给出3d boxed PAP-graph 的纯组合描述,这个问题的可以通过将其正则投影到平面上来解决,但可能会有两种表示方法,一种是扭结的表示方法,一种是虚扭结的表示方法,需要判定,分析两种表示方法的优劣。这一方法的难点在于找到恰当的平面移动(planar moves)集合,就像Kauffman移动集合,还要证明它的有效性。再就是可参考虚纽结的其他组合表示方法,找到3d boxed PAP-graph的最优的组合表示方法。
Joyal-Street拓扑场论的主要困难在于给出3d boxed PAP- graph的纯拓扑描述,可能要借鉴库珀伯格关于虚纽结的唯一表示定理,建立3d boxed PAP-graph的唯一表示定理,加厚曲面的亏格将成为拓扑量子电路的一个复杂性度量。另一个问题,就是研究唯一拓扑表示的可复合性,建立阿提亚类型的拓扑量子场论。
总之,我们的研究目标就是以各类图形演算为基础,建立适用各种情形的一个统一的向上平面性理论。

C. 对偶性,球形性和自旋网络的平面性
对称结构,辫子结构和扭曲结构是张量范畴上自然的范畴性结构,我们前面的研究内容可以证实这些结构的拓扑性(对于扭曲结构,由于时间精力有限我们还未来得及仔细考虑)。接下来,我们就是考虑张量范畴上的常见的对称性:对偶性,球形性,自对偶性和 球形自对偶性,这些都是张量范畴的性质,不是结构。
中枢范畴(pivotal category)C是一类具有对偶性的张量范畴【19】,其特点是其反范畴(opposite category)到其自身具有两个张量等价的张量等价函子(左对偶和右对偶)。我们发现中枢范畴的图形演算将对应于自旋网络(spin network,也称为定向图,或定向网络)的定向平面性(我们还未搜索到图论中有专门定义和研究此性质的文章)。自旋网络具有定向,它的等价关系要保持定向,因此和非定向图的等价关系不一样,例如下面的两个定向平面图是不等价的,但如果忘掉定向它们作为无向平面图就是等价的。

自对偶范畴或者强中枢范畴(我们自己命名,未知有专门术语),是对偶性更强的中枢范畴,其特点是左对偶和右对偶在对象层次上是恒等映射。此时,其图形演算可以用无向网络(无向图)的平面嵌入来描述,其平面性就是普通的平面性。我们认为自对偶范畴可以看做是非对称的cyclic operad的多对象推广。
球形中枢范畴(spherical pivotal category)【19】也是一类特殊的中枢范畴。中枢范畴上存在着一个自然的迹(trace)结构(左迹,右迹),球形范畴是左迹和右迹相等的中枢范畴。此时,其图形演算也是用自旋网络的定向平面性来刻画,但闭图的拓扑性可以扩展到球面嵌入上去。
如果一个中枢范畴既是自对偶的又是球形的,则称为球形自对偶范畴。此时,其图形演算是用无向网络的平面性来刻画,且闭图的拓扑性可以扩展到球面嵌入上去。我们认为球形自对偶中枢范畴可以看做是非对称的modular operad(亏格为零)的多对象推广。下图为这一方面内容的总结。
平行地,我们也可以对诸如对称张量范畴,辫子张量范畴,带子张量范畴等带结构的张量范畴的对偶性,球状性等性质。它们会分别对应各种高亏格的,或者带有虚链环结构的平面性的研究。对于这些平面性,都可以发展和拓扑图论相同的理论体系。概括地说,结构和性质是我们研究图形演算拓扑性的两个基本维度。除此之外,对于张量范畴的分类,后面我们还要介绍全新的分类角度:minor-closed和对称保护的minor-closed。

参考文献:
【1】W.T. Trotter, Jr.: Order preserving embeddings of aographs. Theory and Applications of Graphs, (Proceedings of the International Conference, Western Michigan University, Kalamazoo), Lecture Notes in Mathematics, 642:572-579, 1976.
【2】I. Rival: Reading, drawing, and order. I. G. Rosenberg and G. Sabidussi (eds.) Algebras and orders, NATO ASI Series (Series C: Mathematical and Physical Sciences), Springer, Dordrecht, 389:359-404, 1993.
【3】A.Joyal and R.Street: The geometry of tensor calculus I. Adv. Math. 88(1): 55-112, 1991.
【4】X.Lu, Y.Ye, S.Hu: A graphical calculus for semi-groupal categories. Applied Categorical Structures,April 2019, Volume 27, Issue 2, pp 163-197, arXiv:1604.07276.
【5】X.Lu, Y.Ye: Combinatorial characterization of upward planarity. Communications in Mathematics and Statistics, June 2019, Volume 7, Issue 2, pp 207-223, arXiv:1608.07255.
【6】 L. Kauffman: Introduction to Virtual Knot Theory. arXiv:1101.0665; 或者参考nLab词条:virtual knot theory,https://ncatlab.org/nlab/show/virtual+knot+theory.
【7】T. Fleming, B. Mellor: An Introduction to Virtual Spatial Graph Theory. Proceedings of the International Workshop on Knot Theory for Scientific Objects, OCAMI Studies, Vol. 1 (A. Kawauchi, editor), Osaka Municipal Universities Press, 2007. arXiv:math/0608739.
【8】 G. Di Battista and R. Tamassia: Algorithms for plane representations of acyclic digraphs. Theoretical Computer Science, 61(2-3):175-198, 1988.
【9】 D. Kelly: Fundamentals of planar ordered sets. Discrete Mathematics, 63(2): 197 -216, 1987.
【10】 G. Bertolazzi, G. Di Battista: On upward drawings of triconnected digraphs. Proc. 7th Annu.ACM Sympos. Comput. Geom., 272-280, 1991.
【11】 G. Bertolazzi, G. Di Battista, G. Liotta, and C.Mannino: Upward drawings of triconnected digraphs. Algorithmica. 12:476–497, 1994.
【12】A. Garg and R. Tamassia: Upward planarity testing. Order. 12(2):109–133, 1995.
【13】http://H.de Fraysseix and P.O. de Mendez: Planarity and edge poset dimension. European Journal of Combinatorics, 17(8):731-740, 1996.
【14】C. Auer, C. Bachmaier, F.J. Brandenburg, A. Gleissner: Classification of plane upward embedding. M. van Kreveld, B. Speckmann (Eds.), GD 2011, Lecture Notes in Computer Science, Springer, 7034:415-426, 2012.
【15】P. Angelini, G. Da Lozzo, G. Di Battista, F. Frati, M. Patrignani, I. Rutter: Beyond Level Planarity. Proceedings of the 24th International Symposium on Graph Drawing and Network Visualization (GD 2016), arXiv:1510.08274.
【16】R. Penrose: Applications of negative dimensional tensors. In“Combinatorial Mathematics and its Applications,” (D. J. A. Welsh, Ed.), pp. 221-244, Academic Press, New York, 1971.
【17】 R. Penrose: Angular momentum: an approach to combinatorial spacetime, in T. Bastin (ed.), Quantum Theory and Beyond, Cambridge University Press, 1971, (this paper can be found online on John C. Baez's website http://math. ucr.edu/home/baez /penrose/ ).
【18】A.J. Power: A 2-categorical pasting theorem. Journal of algebra.129:439-445, 1990.
【19】 P. Selinger: A survey of graphical languages for monoidal categories. New structures for physics, Lecture Notes in Physics, Springer, 813:289-355, 2011.
【20】S.Hu, X.Lu, Y.Ye: Combinatorics and algebra of tensor calculus. arXiv:1501.01790. 未发表,其中对于monadic性质的讨论有问题,需要进一步研究.
【21】K. Kawarabayashi, B.Mohar: Some recent progress and applications in graph minor theory. Graphs and Combinatorics, 23 (1): 1-46, 2007.
【22】N. Reshetikhin, V. Turaev: Invariants of 3-manifolds via link polynomials and quantum groups. Invent. Math. 103 (3):547-597, 1991.
【23】A. Zorich: Flat surfaces. arXiv:math/0609392.
【24】D. Kelly and R. Rival: Planar lattices. Canadian Journal of Mathematics, 27: 636 -665, 1975.
【25】 B. Mohar and P. Rosenstiehl: A flow approach to upward drawings of toroidal maps. In: Graph Drawing (R. Tamassia and I. G. Tollis, Eds.), Lecture Notes in Computer Science, Springer-Verlag, New York, 894:33-39, 1995.
【26】B. Mohar: Straight-line representations of maps on the torus and other flat surfaces. Discrete Mathematics, 155:173-181, 1996.
【27】B. Mohar and P. Rosenstiehl:Tessellation and visibility representations of maps on the torus. Discrete & Computational Geometry, 19:249-263, 1998.
【28】 X.Lu: Planar order on vertex poset. Journal of university of science and technology
of china, November, 2018, Volume 48, Issue 11, pp 902-905, arXiv:1901.04142.
【29】D. Kelly: On the dimension of partially ordered sets. Discrete Mathematics, 35: 135-156, 1981.
【30】G. Kuperberg: What is a virtual link? Algebra & Geometric Topology, 3:587-591, 2003.
【31】M.A.Levin and X.G.Wen: String-net condensation:a physical mechanism for topological phases. Phys.Rev.B 71 (2005) 0405110, arXiv:cond-mat/0404617.
【32】G.Vidal: Entanglement renormalization: an introduction, chapter of the book “Understanding quantum phase transitions”, edited by Lincoln D.Carr (Taylor & Francis, Boca Raton 2010), arXiv:1210.1281.
【33】Seramika Ariwahjoedi, Jusak Sali Kosasih, Carlo Rovelli, Freddy P. Zen,: How many quanta are there in a quantum spacetime?, Classical and Quantum Gravity 32(16), April, 2014, arXiv:1404.1750.
【34】J.C. Baez: Spin Network States in Gauge Theory, Adv. Math.117 (1996) 253-272,
arXiv:gr-qc/9411007.
【35】J.Ehlers, F.A.E.Pirani, A.Schild: The Geometry of Free Fall and Light Propagation,
in General Relativity, ed. L.ORaifeartaigh (Clarendon, Oxford, 1972).
【36】A. Delpeuch, J. Vicary: Normalization for planar string diagrams and a quadratic equivalence algorithm, arXiv:1804.07832.
【37】G.Da Lozzo, G.Di Battista, F. Frati, M. Patrignani and V. Roselli: Upward Planar Morphs.In: T.Biedl, A.Kerren (eds), Graph Drawing and Network Visualization. GD 2018. Lecture Notes in Computer Science, vol 11282. Springer, Cham.
【38】P. Selinger: A survey of graphical languages for monoidal categories. New structures for physics, Lecture Notes in Physics, Springer, 813:289-355, 2011.
