概率图模型简要笔记（一）

今天在B站看到了一个机器学习白板推导的系列视频，感觉很不错，然后就看了一下概率图模型，之前啃过PRML这本书，啃得云里雾里的，看视频的时候就记了记笔记。

一. 概览

整个概率图模型的核心问题：高维随机变量

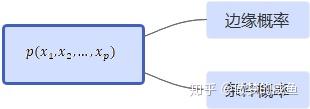
对于高维随机变量，两个基本法则分别对应这两个基本问题：

加法（积分）——边缘概率：

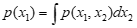
乘法——条件概率：

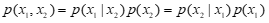
根据两个基本法则可以推出两个常用的法则：

链式法则：

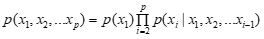
贝叶斯法则：

研究高维随机变量会造成一个问题——计算量巨大

在面对这样的一个问题是，我们通常都是简化它，假设他们是相互独立的，彼此之间互不相干，有一个典型的算法：朴素贝叶斯算法，也就是假设各个维度相互独立。

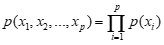
这个假设过于强了，因此，需要重新假设，那么就假设它只与一个状态有关，其他状态无关（马尔可夫假设）：

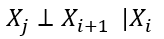
最后这个假设也比较强，因此重新假设，将所有变量分为三个互不相交的集合A,B,C，这样就得到了条件独立性假设：

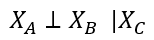
至此整个就得到了概率图中两个要素，研究的问题是：高维随机变量，解决办法是：条件独立性假设。

整个概率图模型需要解决的问题就是：表示、推断、学习以及决策。

二．贝叶斯网络

1.三种基本的拓扑结构：

概率图就是将图赋予了概率定义，可以很直观的根据图结构寻找到概率之间的独立性。

根据独立性假设，我们就可以将复杂的计算简化。

链式法则：

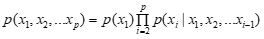
条件独立性：

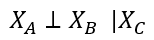
因子分解：

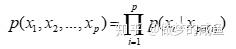
其中： x_{pa(i)} 表示 x_i 的父节点。

根据概率图模型就可以很直观的写出因子分解，图结构的作用就在于很好的表达条件独立性。首先将箭头符号定义如下：

1）tail—tail

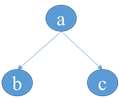
根据因子分解可以很快写出表达式：

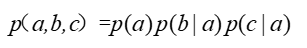
根据链式法则可以得到：

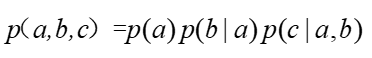
两个公式一对比可以得到：

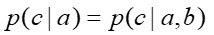
这也就意味着在给定a的前提下，b和c相互独立。如果觉得不够直观，可以继续推导：

这也就直接得到了条件独立的定义：

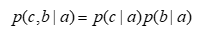
根据这样就得出一条规律：在tail-tail（尾—尾）的拓扑结构中，若a被观察，则路径阻塞，也就是说，b和c相互独立。

2）head—tail

根据因子分解可以写出：

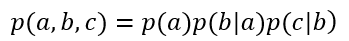
根据链式法则写出：

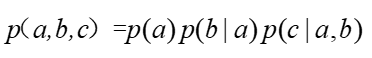
两式对比可得：

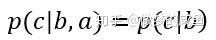
根据这样就得出一条规律：在head-tail（首—尾）的拓扑结构中，若b被观察，则路径阻塞，也就是说，a和c相互独立。

3)head—head

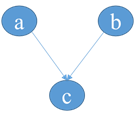
根据因子分解可以写出：

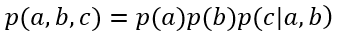
根据链式法则可以写出：

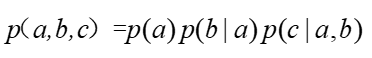
两式对比，可以直接得到：

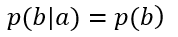
根据这样就得出一条规律：在head-head（首—首）的拓扑结构中，若c未被观察，则路径阻塞，也就是说，a和b相互独立。a和b两者是天然独立的，但是一旦c被观察了，那么两者的独立性就被打破了。当c的后继节点被观察，同样会打破a和b的独立性。

2.D划分

D划分其实就是三种基本拓扑节点关系的一个推广，将节点关系推广到集合关系。

假定集合ABC相互之间不相交，若在A和C之间存在路径节点b，节点b和集合B之间需要满足的关系为：

1. 当b节点的拓扑关系为tail—tail, head—tail这两种类型是，b节点一定存在于B集合当中；

2. 当b节点的拓扑关系为head—head结构时，b节点及其后继节点一定不在B集合当中。

在满足这一关系时，称作 X_A\bot X_C | X_B

D划分的意义在于帮助我们找到了条件独立性，这样也就便于简化计算。

在基于全局节点条件下，求某一个节点的概率问题可以写为：

其中 x_{-i} 表示除去集合中除去 x_i 的所有节点的集合。

\Pi_{j=1}^{p}p(x_j|x_{pa(j)}) 可以分解为与 x_i 有关的和无关的两个部分之乘积，那么对于下面的积分，就可以将与无关的部分提到积分号前，直接约掉，这样就只剩下与有关的部分了。最终可以化为：

可以用图来表示这种关系，该图又被称为马尔可夫毯：

3. 典型的模型

贝叶斯网络总的来说就是两句话：从单一到混合，从有限到无限。单一到混合比较好理解，就直接看上图就好，有限到无限具体指的是空间和时间两者。

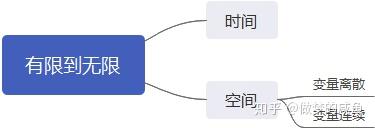
附录：

B站视频链接：