Locally Linear Embedding

最近在看一些降维方面的论文，从一些基础算法的论文开始看起，包括PCA、SparsePCA、KernelPCA、SNE、NCA、LLE等等。目前已经整理了两篇文章，分别为《深入了解PCA》和《Neighbourhood Component Analysis》，前者介绍了一下基本的PCA，以及SparsePCA和KernelPCA，后者介绍了NCA及其代码实现。本文就来介绍一下LLE及其相关的内容。

周老师西瓜书《机器学习》上面也有介绍到LLE、MDS、Isomap等经典降维算法，之前看书也有学习过。既然学过了，为什么还要去看论文呢，看论文是为了更好地去把握提出这个算法的主要思想，即：之前有哪些研究，这篇研究主要解决了什么问题。个人感觉还挺有意思的，一篇论文也就十页左右，不太占用时间。

本文就介绍一下经典的Locally Linear Embedding，简称LLE，作者是Sam T. Roweis和Lawrence K. Saul，发表在《Science》2000上，论文完整题目为《Nonlinear Dimensionality Reduction by Locally Linear Embedding》，整篇论文就占了4页。和LLE高度相关的还有Laplacian Eigenmaps与Hessian LLE。

下面是本文的主要内容：

1. LLE简介和数学表达及求解
2. LLE代码实现
3. 部分实验结果展示
4. Laplacian Eigenmaps
5. 其它关于流形的故事

1 LLE简介和数学表达及求解

1.1 LLE简介

首先界定一下LLE的范畴，它属于降维（Dimension Reduction）与流形学习（Manifold Learning）。首先，从降维角度，LLE可以学习高维数据的紧凑表示（Compact representation），可以把数据从高维空间降维到一个低维空间。另外，从流形学习角度解释，可以通过下面的Figure 1来理解（图片来自论文截图）。其中，图A代表的是二维流形，一个以螺旋卷曲形式嵌入到三维空间的二维平面；图B表示在二维流形上采样得到的数据点。可以把B当作我们观察到的样本，然后我们要通过这些样本来获得真实的数据内在表示。

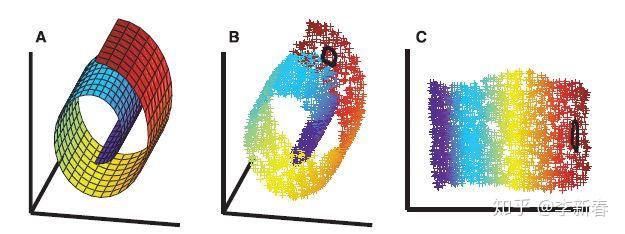
如果直接用PCA来做，是无法将其像扯布一样扯开的（想象卷起来的布匹，把它扯开），这是因为PCA没有考虑样本间局部关系，而是考虑的整体数据的统计信息，所以得到的错误的结果，后面实验会详细展示。而用LLE就可以得到图C的结果，把数据像布匹一样展开。

由于LLE涉及到流形学习，而自己对流形领域的一些基本术语还不是很了解，上面对LLE的解释都是自己读文章之后的理解，可能有不准确的地方。下面附上论文给出的定义，一个我认为是非常简练、准确的概念解释：

Locally linear embedding (LLE), an unsupervised learning algorithm that computes low-dimensional, neighborhood-preserving embeddings of high-dimensional inputs.

下面来介绍一下LLE的主要思想。还是从名字着手，Locally Linear指的是局部线性关系，这里又用到了近邻的思想，用近邻样本来线性加权来近似目标样本；Embedding是指在低维空间学习嵌入表示，保持这些表示的近邻关系和原来的近邻关系基本一致。LLE的总体思想可以概括为两个部分：高维空间近邻线性重构 & 低维空间嵌入表示保持近邻关系。

1.2 LLE数学表达和求解

下面正式 用数学形式来表述LLE的过程，给定数据点集合 X = \{ x_1, x_2, \cdots, x_n\} ，其中每个 x_i \in R^m 是一个 m 维的数据样本，我们要获得 Y = \{ y_1, y_2, \cdots, y_n\} ，其中每一个 y_i \in R^d 是一个在 d 维的样本，并且 d < m。

上面介绍了LLE的主要思想包括两个部分，那么实现的过程可以分为三步来实现：寻找近邻，线性重构，低维嵌入。

• Step 1 寻找近邻

对于每个样本 x_i ，通过欧式距离选择近邻样本，可以通过选择最近的k个点，也可以通过最大距离阈值来选择不固定数量的近邻。LLE使用的是前者。

• Step 2 线性重构

初始化矩阵 W \in R^{n\times n} ，现在考虑样本 x_i ，对于不属于其近邻的样本 x_j ，设置 W_{ij} =0 ；对于属于其近邻的样本 x_j ， W_{ij} 需要通过下面的优化求解：

\epsilon(W) = \sum_{i=1}^n \Vert x_i - \sum_{j \in \mathcal{N}(x_i)} W_{ij}x_j \Vert_2^2 \\ s.t. \qquad W1^n = 1^n

即每个样本都可以由它的 k 个近邻线性加权重构（误差平方和最小），并且满足权重之和为1。下面推导 W_{ij} 怎么求解。由于每个样本由其近邻重构的过程是互相独立的，我们将问题拆分，考虑更一般化的问题。对于样本 x ，利用 k 个近邻 \eta_j 来重构，对应的权重为 w_j ，那么优化问题为：

\min_{w} \qquad \frac{1}{2}\Vert x - \sum_{j=1}^k w_j \eta_j \Vert_2^2 \\ s.t. \qquad w^T1^k = 1
实际上，这就是一个带有约束的线性回归问题。记近邻样本为 N = \left[ \eta_1; \eta_2; \cdots; \eta_k \right] ，有 N \in R^{n \times k} ，上面的问题变为：

\min_{w} \qquad \frac{1}{2}\Vert x - Nw \Vert_2^2 \\ s.t. \qquad w^T1^k = 1

利用拉格朗日乘子法：

\frac{\partial{\mathcal L(w,\lambda) }}{\partial w} = N^TNw -N^Tx -\lambda1^k = 0 \\ \frac{\partial{\mathcal L(w,\lambda) }}{\partial \lambda} = 0 \\ \Rightarrow \\ w = \left( N^TN \right)^{-1}(N^Tx+ \lambda 1^k) \\ w^T1^k = 1 \\

在选取很少近邻，即 k 很小时，以上矩阵求逆不会耗费太多时间，如果矩阵奇异，在对角线加上一个小的常数项。记 C_{js} = \eta_j^T \eta_s ，那么矩阵 C = N^TN ，现在记其逆矩阵为 C^- ，那么有：

w_j = \sum_t C_{jt}^- (x^T\eta_t + \lambda) \\

由 \sum_j w_j = 1 ，推出：

\lambda = \frac{1 - \sum_j\sum_t C_{jt}^-x^T\eta_t}{\sum_j\sum_t C_{jt}^-} \\
将其代入 w_j 即可得到需要的结果。

注：这里还有另外一种推导方法，如果记 C_{jk} = (x - \eta_j)^T(x-\eta_k) ，会有以下结果：

w_j = \frac{\sum_k C_{jk}^-}{\sum_s\sum_k C_{sk}^-} \\

提示：将目标重写为下面的式子（ Tile(x) 表示将 x重复 k 次得到的矩阵 ）：

\Vert x - \sum_{j=1}^k w_j \eta_j \Vert_2^2 = \Vert \sum_j w_j(x - \eta_j) \Vert_2^2 = \Vert (Tile(x)-N)w\Vert_2^2\\

• Step 3 低维嵌入

下面是在低维空间寻找一组数据 Y = \{ y_1, y_2, \cdots, y_n\} ，保持局部线性重构关系得到满足，即优化下面式子最小：

\Phi(Y) = \sum_{i=1}^n \Vert y_i - \sum_{j=1}^n W_{ij}y_j \Vert_2^2 \\

只满足上面的条件还不够，因为如果所有的 y_i = 0 ，那么得到的结果肯定是最小值0，但是却没有任何实际意义。所以，加上下面的约束（ Y 每一维均值为0，方差为1）：

\sum_i y_i = 0^d \\ \frac{1}{n}\sum_{i=1}^n y_i^T y_i = I^{d\times d}

对于第一个均值为零的约束条件，我们可以先不考虑，这是因为 \sum_j W_{ij} = 1 ，所以对所有 y_i 加上一个偏移项不会影响最终的结果。所以考虑下面的问题：

\Phi(Y) = \sum_{i=1}^n \Vert y_i - \sum_{j=1}^n W_{ij}y_j \Vert_2^2 = \Vert Y - WY \Vert_F^2 = tr\left( Y^T(I-W)^T(I-W)Y \right)\\ s.t. \qquad Y^TY = I^{d \times d}

实际上，论文提到上述问题可以通过Rayleitz-Ritz theorem来解决，结果是取矩阵 (I-W)^T(I-W) 最小的d + 1个特征向量，然后去除最后一个全 1 特征向量（对应的特征值是0），然后就得到了 Y \in R^{n \times d} 。至于上述定理是什么以及为什么可以直接推导出结果，作者给了一个1990年的参考书籍《Matrix Analysis》。

下面，通过拉格朗日乘子法来简单看一下为什么会有这样的结果。为了使用拉格朗日乘子法，先看看d = 1时的情况，即低维嵌入时只取一个实数值。

\mathcal L(y, \lambda) = tr\left( y^T(I-W)^T(I-W)y \right) - \lambda (y^Ty - 1) \\ \frac{\partial \mathcal L(y, \lambda)}{\partial y} = 2(I-W)^T(I-W)y - 2\lambda y = 0 \\ \Rightarrow \\ (I-W)^T(I-W)y = \lambda y

所以， y 是矩阵 (I-W)^T(I-W) 的特征向量，如果我们想使得目标最小，那么就选最小特征值对应的特征向量，这里我们不选最小的特征值0，因为它对应的特征向量的元素都是相同的值，所以选第二小的特征值对应的特征向量。

上面只给出了一维情况下利用拉格朗日乘子分析的方法，对于多维的约束如何分析（貌似比较难，限于笔者水平不够，这里先埋个坑），感兴趣的读者可以去查阅一下相关资料。

可以看出，这貌似和PCA的过程很相似，PCA做的是先对数据归一标准化，然后求协方差矩阵，再求协方差矩阵最大特征值对应的特征向量作为第一个主成分的方向。总之，一个结论是特征值和特征向量很实用，当然也很重要。

1.3 LLE小结

LLE主要思想为两个过程 ：高维空间近邻线性重构 & 低维空间嵌入表示保持近邻关系。

• 前者利用了数据的局部性，考虑了数据点与其近邻的关系。这种思想很常见，比如在时间序列分析中一个时刻的数据往往和其前面几个时刻的数据相关；通过数据点近邻关系构建一张图的思想也很常见，比如后面介绍的Laplacian Eigenmaps。另外，LLE和NCA也有一定的相似之处，回顾一下NCA，NCA是有监督的、基于Stochastic 1-NN分类器、利用可学习的马氏距离来学习相似度、使用Leave-One-Out验证方法来训练的一种降维和度量学习的方法（更多可以参考《Neighbourhood Component Analysis》）。从这个角度，LLE的第一步做的是利用k-NN解决多变量回归问题（利用近邻样本拟合目标样本的过程是一个回归问题）。
• 后者主要思想是低维空间数据点的某些统计特性和高维空间的一致。这种思想在SNE和T-SNE中得到了充分的体现。另外，在很多生成模型（Generative Model）里面，有很多会利用这种思想。比如，在纹理合成（Texture Synthesis）任务中，给定一张纹理图片，要生成一个和这张纹理图有一样的风格但不完全相同的纹理图，很经典的一种做法是：先生成一张随机图片，然后经过一些特征提取过程（传统特征描述子 & 神经网络），得到一个低维空间的表示，根据这个表示计算一些统计量（比如Gram Matrix），优化目标是使这个随机图的统计量要和目标纹理图的统计量尽可能一致，构建平方和误差然后更新随机图，使误差越来越小即可。

2 LLE代码实现

LLE的简单代码实现很简单，按部就班地按照上面的算法流程来求解即可，当然真正工程上实现还要保证速度、鲁棒性与数值稳定性等等。这里就给出简单的实现Demo，工程上的代码实现可以参考sklearn.manifold里面的LocallyLinearEmbedding实现。

下面的实现主要包括：求近邻、求矩阵 C （利用第二种推导方式）、求 W 、求特征向量。

class LLE():
    def __init__(self, k_neighbors, low_dims):
        '''
        init function
        @params k_neighbors : the number of neigbors
        @params low_dims : low dimension
        '''
        self.k_neighbors = k_neighbors
        self.low_dims = low_dims

    def fit_transform(self, X):
        '''
        transform X to low-dimension
        @params X : 2-d numpy.array (n_samples, high_dims)
        '''
        n_samples = X.shape[0]
        # calculate pair-wise distance
        dist_mat = pairwise_distances(X)
        # index of neighbors, not include self
        neighbors = np.argsort(dist_mat, axis = 1)[:, 1 : self.k_neighbors + 1]
        
        # neighbor combination matrix
        W = np.zeros((n_samples, n_samples))
        for i in range(n_samples):
            mat_z = X[i] - X[neighbors[i]]                 # x - \eta_i
            mat_c = np.dot(mat_z, mat_z.transpose())       # C
            w = np.linalg.solve(mat_c, np.ones(mat_c.shape[0]))
            W[i, neighbors[i]] = w / w.sum()

        # sparse matrix M
        I_W = np.eye(n_samples) - W
        M = np.dot(I_W.transpose(), I_W)

        # solve the d+1 lowest eigen values
        eigen_values, eigen_vectors = np.linalg.eig(M)
        index = np.argsort(eigen_values)[1 : self.low_dims + 1]
        selected_eig_values = eigen_values[index]
        selected_eig_vectors = eigen_vectors[index]

        self.eig_values = selected_eig_values
        self.low_X = selected_eig_vectors.transpose()
        print(self.low_X.shape)
        return self.low_X

3 部分实验结果展示

先来看看对于下面二维的数据进行降维的过程，使用PCA和LLE来对比实验。下图Figure 2展示的是一个嵌入到二维平面中的一维曲线，构造方法是按照曲线 \rho = 1 + \theta ，随机生成的9000个数据点，每个颜色中选择3000个数据点。加上颜色是为了方便观察效果，实际使用PCA和LLE进行降维过程中不会用到颜色标记信息。

利用PCA和LLE取得的结果为Figure 3，第一张是PCA的结果，运行得到的主成分向量为（-0.989, -0.146），将所有数据点往这个向量上投影，可以看出蓝色的数据点基本上被黄色数据点覆盖；后面两张是LLE的结果，近邻数目分别取10和20，可见后者得到的结果基本上是我们需要的“扯开”效果，同时也可以看出近邻数目的选择对最终结果的影响很大。

下面看一下对于三维的数据点，即文章开始给出的二维流形嵌入到三维空间的结果，构造数据集如Figure 4，也是通过曲线 \rho = 1 + \theta采样，然后z轴随机采样得到的。生成数据的代码为：

class ManifoldData():
    def __init__(self):
        pass

    def spiral3D(self, a = 1.0, b = 1.0, begin_circle, end_circle, num_points):
        theta = np.random.uniform(low = 2 * begin_circle * np.pi, 
                                  high = 2 * end_circle * np.pi, 
                                  size = (num_points, ))
        radius = a + b * theta
        xs = radius * np.cos(theta)
        ys = radius * np.sin(theta)
        zs = np.random.uniform(low = 0.0, high = 10.0, size = (num_points,))
        return [ys, zs, xs]

ma = ManifoldData()
data1 = ma.spiral3D(begin_circle = 0.0, end_circle = 0.5, num_points = 5000)
data2 = ma.spiral3D(begin_circle = 0.5, end_circle = 1.0, num_points = 5000)
data3 = ma.spiral3D(begin_circle = 1.0, end_circle = 1.5, num_points = 5000)

生成的数据为Figure 4：

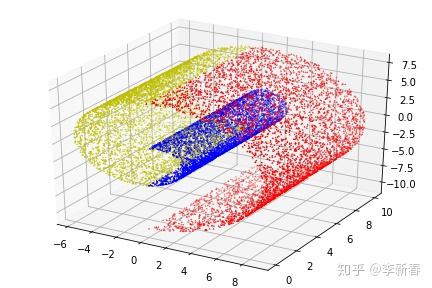
使用PCA得到的结果为：三个主成分向量分别为（0.560, -0.011, -0.828）、（0.828, -0.006, 0.560）与（-0.007, -0.999, 0.009），三个主成分的方差比例分别为0.469，0.355与0.175。结果如Figure 5所示，PCA-1-2是指使用第1与第2个主成分，其余同理。可以看出，在第一张图中，PCA完全抹灭了z轴的数据信息，第二、三张图片使得红蓝黄数据点交错在了一起。

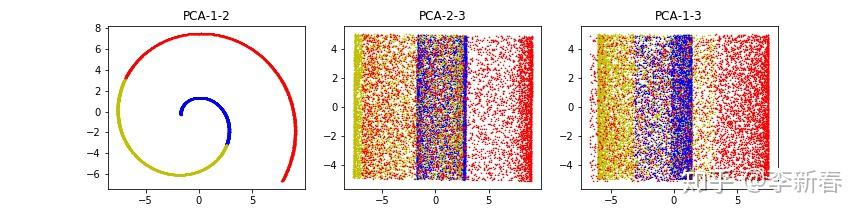
使用LLE的结果如下，取40个近邻，可以看出基本上是将数据“扯开”了，但是为什么会出现蓝色倾向于纵向分布而红色倾向于横向分布的奇怪形状，笔者很好奇，不过总之相比于PCA效果还是不错的。

4 Laplacian Eigenmaps

Laplacian Eigenmaps是一个和LLE特别相似的流形学习的方法，后文简称LE。LE是在LLE后面出来的一项工作，论文题目为《Laplacian Eigenmaps for Dimensionality Reduction and Data Representation》，这篇论文给出了两个特别有意思的地方：

• Laplacian Eigenmaps的主要思想来源于物理领域热力学中的Heat Equation
• 在Manifold上使用Laplace Beltrami Operator等价于Graph Laplacian

第一条涉及到物理学领域，并不是很了解，所以就没有去仔细看；第二条看了一段时间，发现对流形的一些基本性质不是很了解，所以文章中很多等式的转换就觉得莫名其妙。所以，下面还是把重点放在Laplacian Eigenmaps的算法过程上，以及为什么这么做可以达到比较好的降维和数据表示效果。

下面先介绍Laplacian Eigenmaps具体操作过程：

• Step 1 寻找近邻，构建邻接图

同LLE，这里可以通过 \epsilon -neighborhoods和k-nearest-neighbors来选择近邻。对于前者，如果 x_i 是 x_j 的近邻，那么反过来亦然，对于后者则没有这种对称性，所以为了满足对称性，后者放松约束，只要使得 x_j \in \mathcal N_k(x_i) 或者 x_i \in \mathcal N_k(x_j) 即可认为有一条边；前者可能会导致图中产生许多个小的连通分量，而后者不会。

将每个数据点看作一个顶点，将近邻对用一条边连接起来，这样就构成了一张图，准确来说如果利用k-nearest-neighbors的方法来选择近邻对，得到的是一张有向图，但是经过上面加粗部分的操作，可以看作是无向图。

• Step 2 给边赋权值，构建带权图

根据顶点之间的关系来给图之间赋权值，有以下两种方式。第一种，利用Heat Kernel，即：

W_{ij} = \exp \left( -\frac{\Vert x_i - x_j \Vert_2^2}{t} \right) , \qquad Connected(x_i, x_j)\\ W_{ij} = 0, \qquad NotConnected(x_i, x_j)

另外 一种方式就是简单地取 1 和 0，即：

W_{ij} = 1, \qquad Connected(x_i, x_j)\\ W_{ij} = 0, \qquad NotConnected(x_i, x_j)

当 t \rightarrow +\infty ，两者等价。一般来说选取第一种方案比较好。得到的 W 是对称阵。

• Step 3 Eigenmaps

计算图的Laplacian Matrix，即 L = D - W ，其中 D_{ii} = \sum_j W_{ji} ， D 是对角矩阵，第 i 个对角元素是图权值矩阵 W 第 i 列的和。下面计算广义特征值问题：

Lf = \lambda Df \\

取 最小的d + 1个特征值对应的特征向量，去除最小的特征值 0 对应的特征向量，得到：

Y = [f_1; f_2; \cdots; f_d] \in R^{n\times d} \\

上面给出了Laplacian Eigenmaps的算法过程，可以看出其主要思想是：寻找近邻，构建邻接图，Laplacian Matrix特征值分解。和LLE的过程比较相似，只不过LLE是基于近邻重构的思想，而LE在做什么我们目前还不清楚，所以下面来看看LE背后的原理是什么。

LE首先将数据点转换为一张图 G = (V, E) ，近邻样本之间有一条边，是无向图，并且每条边都有权重。LE要做的就是在低维空间寻找一组表示 Y = [y_1;y_2;\cdots;y_n]^T \in R^{n\times d} ，使得近邻关系和高维空间尽可能一致 ，假如 x_i 与 x_j 离得比较近（ W_{ij} 比较大），那么对应的 y_i 与 y_j 也应该比较近（如果二者离得远，那么乘以 W_{ij} 带来 的损失就会很大），所以使用下面的优化方案：

\min_Y\frac{1}{2}\sum_{i=1}^n \sum_{j=1}^n W_{ij}\Vert y_i - y_j \Vert_2^2 \\

而上式使用矩阵形式即为：

\min_Y\frac{1}{2}\sum_{i=1}^n \sum_{j=1}^n W_{ij}\Vert y_i - y_j \Vert_2^2 = \min_Y \frac{1}{2}tr\left( Y^T(D-W)Y\right)\\

同样道理，我们也对 Y 施加一个约束：

Y^TDY = I^{d\times d} \\

这是对不同的 y_i 要求不同的模的大小，因为图中有的结点比较重要（ D_{ii} 比较大 ），相反有的则不是很重要。给定上面的优化目标和约束条件，问题就可以转化为求广义特征值问题：

Lf = \lambda Df \\
总结：LLE做的是最小化 tr\left( Y^T(I-W)^T(I-W)Y \right) ，这是通过“低维空间的近邻重构性质要与高维空间的近邻重构性质保持一致”推导出来的；LE要做的是使 tr\left( Y^T(D-W)Y \right) 越小越好，这是通过“在高维空间 构建带权邻接图，然后寻找一组表示使得图的性质得以保持”推导出来的。

5 其它关于流形的故事

现实中，很多数据都和流形有关，比如图像。对于同一个物体，从不同角度拍摄得到的一系列图片实际上是分布在一个低维流形中的。如何将图像降维到低维空间呢？很多方法，比如AutoEncoder，GAN等都是为了找到图像的真实流形分布（Intrinsic Manifold），从而达到生成图像的目的。

这就产生比较有趣的事情了，假设我们现在知道有两张图片在低维流形上的数据点，那么在流形上对这两个点插值得到新的数据点，这些新的数据点对应的图像是什么样的呢？这个过程叫做“流形漫步”，英文是Walking On the Manifold。这项研究在GAN的文章里面很常见，比如DCGAN中的一幅图如Figure 7，图中每一行都是在流形上相邻插值的数据点生成的图片，比如最后一行，生成的图像从室内电视机逐渐变成了窗户。

还有很多其它关于流形的有意思的事情，本文就不展开了。

文中相关代码见：

参考文献

1. Sam T. Roweis, Lawrence K. Saul. Nonlinear Dimensionality Reduction by Locally Linear Embedding, Science 2000.

2. Locally Linear Embedding

3. https://cs.nyu.edu/~roweis/lle/papers/lleintro.pdf

4. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation

5. Alec Radford, Luke Metz, Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks, CoRR 2015.