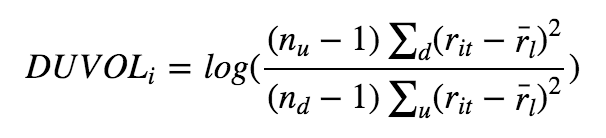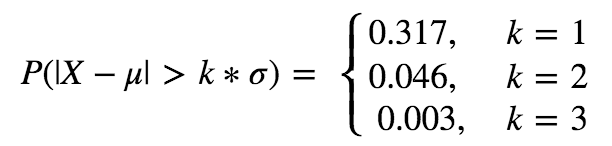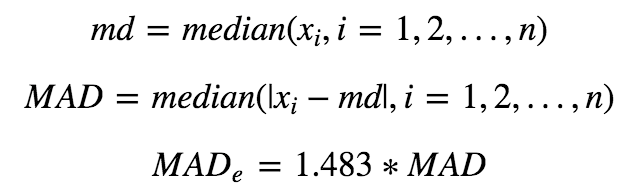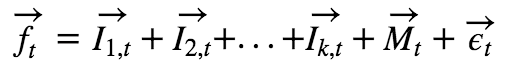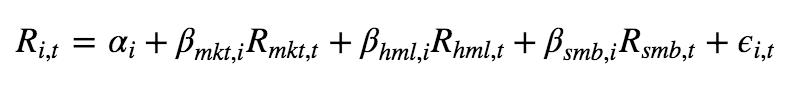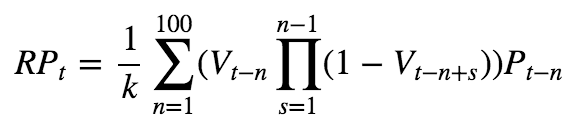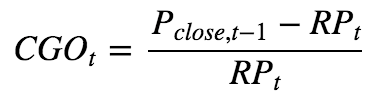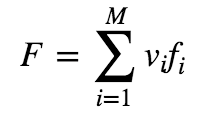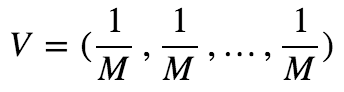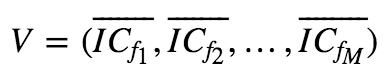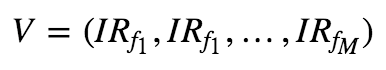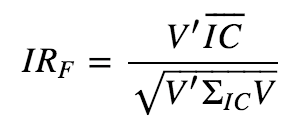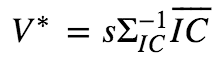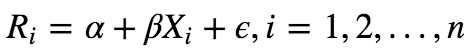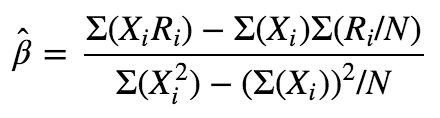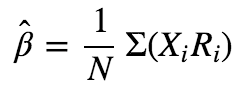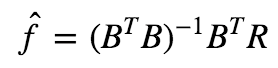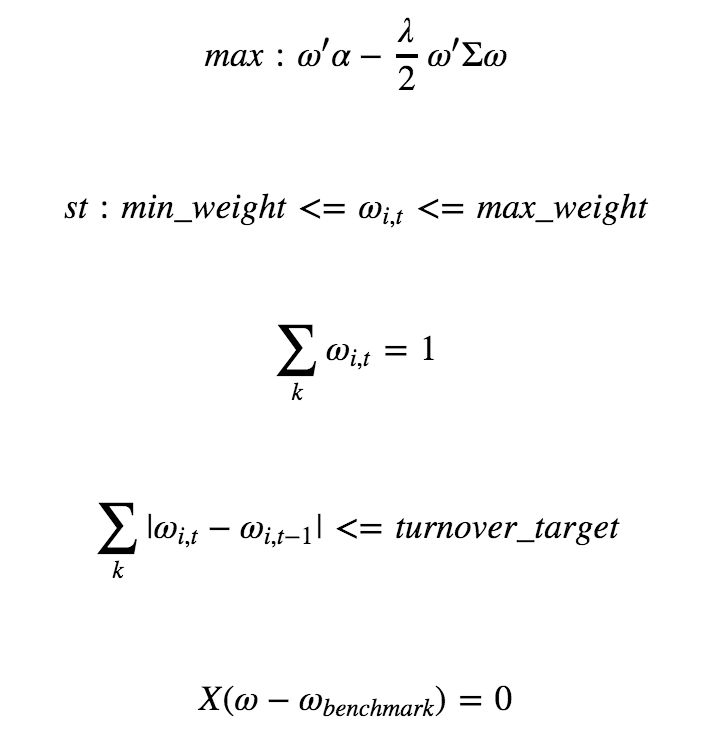【矿友必读】一个量化少年的年度因子研究总结

2018 年 1 月 2 日 优矿量化实验室 磊少

引导关注商务学习

本帖主要是围绕2017年所做的研究总结，全文分别从Alpha模型、风险模型、优化器三个角度依次展开，蓝色标注为详细解读文章，因公众号受限无法直接跳转链接，矿友们可直接点击文末“阅读原文”移步到优矿社区继续阅读，最后衷心感谢各位矿友在2017年的支持与陪伴，2018，我们再接再厉！

先说感谢，2017年特别想感谢几个人，有未曾谋面的，也有在身边的。首先是学习上，其实自从决心做量化之后，就经常看东方证券朱剑涛老师的研报，朱剑涛老师的研报内容丰富，体系完整，思维严密，每一篇读完都很有收获，对我了解多因子这个体系帮助很大，所以很想感谢朱剑涛老师，虽然未曾谋面过。还有就是小伙伴们，小伙伴们都在券商资管做量化，很多多因子模型不懂的问题都会直接向他们请教，他们也给了很多建议，对我帮助也很大。还有就是魏老师，魏老师手把手教我风险模型，有了风险模型，自己也算是有一技之长吧。工作上最想感谢领导，自己今年刚毕业，领导很照顾我，有不开心的会开导我，我做的哪里不对，也会及时帮我指出，我今后也会再接再厉，不让他失望。然后就是所在的团队，大家对我都很亲切，有种家的感觉，非常希望我们团队可以一直这样下去，2018，充满希望的一年。

2017年刚刚结束，每年这个时候我都会去回顾今年自己收获了什么，失去了什么。这一年，对我来说其实内心还是挺复杂的，从某种意义上来说，它宣告了我青春的结束。我不知道对大家来说，怎么去定义青春的结束，从我的角度来说，当我喜欢了八年的人最终还是选择其他人的时候，我知道我青春真的结束了，从今以后，自己要开始一段新的旅程了。那么这一年收获了什么？我想也收获了很多，收获了新的朋友，增长了自己的知识，最重要的是自己在成长，我很讨厌自己踏步不前。

心路历程讲完，之所以写这篇文章，一方面是应组织要求，而另一方面，我想确实需要总结一下这一年的收获，同时分享给一直支持我的广大矿友。最后祝大家在新的一年里，再接再厉，厚积薄发，一飞冲天！

2Alpha模型

Alpha模型，用来预测组合收益的模型，或者说是获取超额收益的模型。简单来说，每个因子可以理解为股票的一个属性，就像人一样，身高、体重、money等等。有的人高，有钱，那么更加容易受到大家的青睐，我们就是要把这些人找到，嫁给他，走上人生巅峰，股票也是一样的道理。Alpha模型可以帮助我们去筛选这样的一类股票，获取超额收益。

2.1【上下行波动率因子】

这是一个技术指标类的因子，它的构建逻辑如下：上下行波动率是历史收益率低于平均收益率的下行波动率比上历史收益率高平均收益率的上行波动率的比率。

其中，n(u)为大于平均复合收益率的天数，n(d)为小于平均复合收益率的天数, r(it)为股票的日收益率。这是一个衡量股价暴跌可能性的指标，学界通常认为DUVOL较高的股票有着更高的暴跌可能，因此也就有着期望更高的风险溢价。需要注意的几点：

为了计算方便，文中使用的是有偏的日波动率；
本文的价格即当日真实的收盘价格；

这个因子和市值，反转因子均有明显的相关性，当时回测的时候还是到2017年初。从当时的回测结果来看，表现非常优异，五分位组区分度较高，对冲后年化超额收益达到15.3%，最大回撤9%，IR大概有2.6左右。当然，如果使用归因分析，应该可以得到组合的超额收益来源于在这个反转因子上的暴露这样的结论。

2.2 【选股因子数据的异常值处理和正态转换】

这篇文章，主要介绍了一些异常值处理的方法，我这里一起总计下数据预处理需要做的一些步骤：

2.2.1 去极值

分位数去极值：优矿提供的去极值的函数中的功能的一个，把高于上分位数，低于下分位数的点进行拉回。对于分位数去极值方法，我们需要主观的给出上下分位数，既然是主观，那么到底哪个值合适呢？给小了可能达不到去极值的效果，给大了又会带来样本信息的损失，只能给个经验的值；
3sigma法：这种想法的思路来自于正态分布，假设X∼N(μ,σ^2)，那么：

通常把三倍标准差之外的值都视为异常值，不过要注意的是样本均值和样本标准差都不是稳健统计量，其计算本身受极值的影响就非常大，所以可能会出现一种情况，那就是我们从数据分布图上能非常明显的看到异常点，但按照上面的计算方法，这个异常点可能仍在均值三倍标准差的范围内。因此按照这种方法剔除掉异常值，经常需要重复多次，可以看到优矿的去极值函数也提供了重复次数这一参数。
中位数法：中位法是针对均值标准差方法的改进，把均值和标准差替换成稳健统计量，样本均值用样本中位数代替，样本标准差用样本MAD（Median Absolute Deviation）代替：

通常把偏离中位数三倍以上的数据作为异常值。和均值标准差方法比，中位数和MAD的计算不受极端异常值的影响，结果更加稳健，更加推荐使用。

2.2.2 中性化

中性化，用来消除因子在行业或者风格的上偏好，为了减少行业或者风格所带来的风险，需要对因子进行中性化的处理。一般把需要中性掉的因子作为因变量，把行业哑变量和市值作为自变量，进行回归，取残差，用公式表示如下：

f(t)表示t时刻因子在N个股票上的取值；
I(k,t)表示t时刻第k个行业在N个股票上的取值，使用0，1哑变量进行表示；
M(t)表示t时刻市值取自然对数并进行横截面标准化之后（风险模型SIZE）的在N个股票上的取值；
取ϵ(t)作为中性化之后的因子值。

优矿也提供了中性函数，因此这一步我们不需要自己做

2.2.3 标准化

做这一步原因有两个，不同的因子可能量纲不一样，把因子通过均值方差的方法转为zscore，才能将因子纳入多因子模型当中。但是有个前提假设是说，最好因子的分布是服从正态的分布的，否则，样本偏度和峰度的影响会使得个股在某一个因子上的得分明显偏大或偏小。那么最好需要进行正态的转化处理，常见的方法有取对数（例如市值），还有box-cox转换，还有一个方法，也会被用到，使用正态分布的逆函数强制进行转换，这种方法，只保留因子的序的信息，忽略了距离信息。

2.3 【特质波动率与特异度】

这是一个很奇怪的现象，大家知道，一般来说风险与收益是成正比的，风险越高，收益越大。但是个股的特质波动率与随后的股票的收益却呈现出负相关的关系，因此又称为特质波动率之谜。现在大概有这样几种解释：

第一类，归因于投资者的博彩型偏好（投机程度）；
第二类，归因于各种形式的市场摩擦；
第三类，无法归类到前两类的解释具体来说，这个因子的构建方式如下：

每个月底回归如上方程，残差的波动率称之为特质波动率，方程的拟合优度称为特异度。本文也对该因子进行测试，实证发现，这两个因子都和反转因子高度相关，好吧，然而反转因子历史上又是个极强的Alpha因子，因此，可以说该因子的超额收益是反转效应带来的，可以归结到反转因子这一类当中。

2.4 【Alpha因子库的精简】

写这篇帖子，当时是应优矿社区一个朋友的要求。其实也很有必要，特别是因子那么多，很多信息都有重复，如果一个因子能被我当前的因子库的现存的因子信息所解释，那么就没有再加入的必要。否则要花人力去维护，但是对模型的改进却没有任何作用。筛选的流程如下：假设总共有k个备选的alpha因子F(1),F(2),...,F(k)，我们已经从中筛选出了s个因子F(i(1)),F(i(2)),...,F(i(s))（初始时s为0），第s+1次筛选流程如下：

step1：对于剩余备选的alpha因子，每个因子每个月都对F(i(1)),F(i(2)),...,F(i(s))做多元回归，计算残差项(s = 0 时不用做这一步)。记得到的K-s个残差项因子分别为θ(1),θ(2),θ(k−s)；
step2：分别把θ(j),j=1,2,...,k−s和F(i(1)),F(i(2)),...,F(i(s))一起做自变量，做Fama-MacBeth回归，记录θ(j)系数的显著性，和每个月横截面回归R^2的平均值；
step3：把系数不显著的因子剔除出备选alpha因子库；
step4：选取系数显著且平均R^2最大的因子，假设为θ(h)，则把该因子作为第s+1个筛选出的因子F(i(s+1))，进入第s+2次筛选；
Step5：如果所有因子的系数都不显著，则停止筛选过程。

注意：这里R^2应该用调整后的，因子筛选第一步不是随机选择一个因子，应该对每个因子进行一次Fama—Macbeth检验，选择参数显著，并且调整后的R^2最大的那个因子。

2.5 【处置效应——CGO因子】

写这篇帖子，有两个地方，一个是当时有个老师来公司讲课，讲的就是行为金融学，恰好有一个同学发了一篇相关的广证券的关于这个因子的PPT，因此就在优矿上进行了实现。因子的计算逻辑如下：

参考价格（reference price）

我们需要找到投资者行为发生突变的一个参考价格。当价格发生突变后，投资者相应的会有所行为。那么对于每个人来说，这样的价格是否是一致的，或者说该如何度量？
显然投资者心中的参考价格与过去买入的成本价有关，并且与昨日的市价有关。如果以均线作为参考价格，只包含了股价最近的信息，却丢失了过往的交易信息。
以Grinblatt（2005）提出的以260周交易数据定义的参考价格（RP）计算公式为基础，考虑到A股市场短线交易者众多，研报提出了如下的基于过去100日成交均价按照换手率加权平均的RP的算法：

式子中的k为权重归一化系数，P(t−n)为过去t-n日的成交均价，V(t−n)为换手率。采用前复权价格计算。过去某一天换手率越大，之后换手率越小，携带的信息对未来越有效。

资本利得突出量（Capital Gain Overhang）

CGO(t)表示第t日这只股票市场持仓者相对参考价格（RP）的平均盈亏情况，CGO(t)越大浮盈越大。

从这上面两个公式看，参考价格的计算还是挺复杂的，需要用到连乘，而且每期权重都不一样，实际计算起来也比较耗时间。另外目前还没有成交均价（VWAP）这个数据，需要自行计算，这个算起来很快，不难。这个因子，和反转因子的相关系其实也比较高，我们也可以从最后计算的公式看出来，只不过，反转因子使用的是20日前的价格，而它使用的是一个由过去100日成交均价衍生计算出来的一个参考价格。因子计算的结果应该与研报类似，我们这边测试的结果也反映了它与反转相关这一点。历史上表现非常稳健，今年一直在回撤。

2.6 【新因子探索——择时因子】

这篇文章来自于东北证券的年度策略总结那篇研报，实现之前，感觉作者说的也很有道理。主要要从行业中性说起，行业中性就是我刚前面所说的中性化步骤做的，只不过这里没有考虑到风格，好比在每个行业中做标准化，这么做的目的在于，某些因子例如财务，估值，这些和行业市值密切相关的因子，不同行业之间是不能直接比较的，而行业中性可以使不同行业之间的因子值具有可比性，说法其实和我之前说的差不多，不这么做，那么你的因子可能存在行业或者风格的偏好。那么文章就举了复星医药和恒瑞医药这两个例子，如果做横截面上的行业中性，以PE为例，恰好得出与我们前面认知相反的一个结论。这表明传统的横截面标准化有些问题，因此我们需要转换思路，例如进行时间序列上的标准化，或者度量当前PE在历史上的水平，再进行横截面上的比较，非常有道理。

衡量时间序列上的高和低的方法很多，我们这里仅选择较为简单的一种方法：分位数法，即计算过去一段时间序列上的当前因子值分位数，把因子的绝对值映射成[0,1]区间的百分数。这里时间周期我们选择过去3年、5年、10年。不选择全历史的原因在于不同股票起始时间不同，无法保证时间段的可比性。这个分位数法，就是我前面提的正态转换的一种做法。

我也进行了因子的计算和测试，从结果来看，Alpha有15.7%，信息比率达到2.87，对冲后最大回撤6%，历史上表现还是非常稳定的，五分位组区分度也很高。今年同样也是一直在回撤。

题外话，有人问我是否需要看因子的多空收益的表现，我还特别请教了港大的一个教授。一般来说，有的因子空头收益比较多，但其实我们并不能获得这块的收益，不过，我们将其纳入多因子模型当中，假设有一个因子要多这只股票，但是这个因子给我们的信息是空这只股票，那么最后就会导致我们最终没有多这只股票。从这个角度来说，这个因子能够为模型带来额外的信息。

2.7 【因子加权简介】

常见的因子加权方式有等权，IC加权，IC_IR加权，最优化IC_IR加权，孰优孰劣，结论不一：

假设现有M个因子f(1）,f(2),...,f(M)，合成后的因子为F，则

等权：每个因子配相同的权重
优点：直观，简单，方便
缺点：没有考虑因子有效性，稳定性以及因子之间的相关性。
IC均值加权：取因子过去一段时间的IC的均值为权重：
优点：考虑了因子有效性的差异
缺点：没有考虑因子的稳定性以及因子之间的相关性。
IC_IR加权：取因子过去一段时间的IC均值除以标准差作为当期因子fi的权重，即权重向量：
优点：考虑了因子有效性的差异，稳定性
缺点：没有考虑因子之间的相关性。
最优化复合IC加权：指最优化复合因子F的IR后得到的最优因子权重进行加权：
解得：
其中s为任意常数
优点：考虑了因子有效性的差异，稳定性，相关性
缺点：因子收益率协方差矩阵估计难度较大

目前，也在研究通过神经网络进行因子的合成，思路来自于华泰的一篇研报，也实现了使用LSTM，RNN，GRU三个模型进行因子合成。但是对于这些非线性的模型，很难去解释最后得到的因子，特别是70个因子丢到模型里面，参数又多，不建议使用。我更倾向于使用传统的线性的方法，特别是我们赌市场风格的时候，也知道在模型里多配哪一类的因子。

推荐下call神的一篇帖子，很不错，MultiFactors Alpha Model - 基于因子IC的多因子合成 ，说的很细。（优矿社区搜索标题即可阅读）

3风险模型

好了，终于讲我主要的工作了，其实基本面风险模型是上半年的工作，下半年花一部分时间在做统计风险模型，目前也有些思路和成果，大家要是有兴趣可以分享给大家。先说说为什么要做风险模型，大概基于这三点来考虑：

首先，你们可曾想过，优矿的中性化函数里头，那些风格因子从哪里来的？没错，来自于风险模型，也就是是说Alpha因子中性化的风格及行业数据是由风险模型提供的；
不知道大家有没有做过组合优化。我也和一些基金经理交流过，为组合添加一个跟踪误差约束是一个常见的需求，但是加了这个约束，需要去估计股票之间的协方差矩阵，传统的估计方法是拿股票的历史收益序列来做估计，粗略来看，没有太大问题，但是当你股票数量多，特别是全市场选股的时候，问题就来了？这时候，为了保证组合优化有解，你要让你选择的时间窗口大于股票的数量，3000只股票，如果用日度的数据的话，要10多年的数据，这不可取，那怎么办，取更加高频的数据，例如，用分钟线，小时线，等等用高频的数据预测低频，噪音很多。算一算需要估计的参数有多少个？N只股票，有N*(N+1)/2个参数需要估计，在实务中显然不能直接使用。风险模型提供了一种类似降维的思想，把原先估计股票的协方差矩阵转为股票行业因子，风格因子的协方差矩阵上去，减少估计的参数的个数，从而提供预测的准确性；
还有一个功能，最近也用的比较多，就是归因分析，魏老师已经分享了好几篇帖子来讲如何使用风险模型对一个基金产品进行业绩归因。所以风险模型的还有一个作用是它可以对组合的收益进行解释，看看是哪一部分。

3.1 因子收益率

为什么要说因子收益率这个概念的，这个和我们讲风险模型有很大的联系。在一些券商研报上，经常会看到因子收益率这一概念，他们使用的是多空收益作为因子的收益率，例如做多得分最高的一组股票，做空得分最低的一组股票。但这个只是用到顶部和底部的少量股票，不够反映因子在全市场的选股能力。更全面反映因子收益率的方法是将因子收益率先进性标准化得到zscore，以zscore为权重构造多空组合，这个组合的收益率叫做因子收益率。这个因子收益率和Fama-MacBeth横截面回归息息相关。假设有N个股票，Ri表示未来一期股票的收益率，做横截面回归：

得到β的ols估计为：

由于X(i)是标准化之后的zscore，所以Σ(X(i))=0，Σ(X(i)^2)=N，于是:

明白为什么叫因子收益率了吗，知道为什么不叫回归系数了吧？理解了这个之后，后面就好说了。也就是说，如果对单个因子做一元的Fama-MacBeth回归，再在时间序列上检验β的显著性等价于对该因子的因子收益率做t检验，这是显然的。

但是Barra的风险模型里面是个多元回归啊，还是有些不一样的。这里又引入了一个纯因子收益率的概念，纯因子收益率的大小对应着多因子模型，不同的多因子模型，单个因子的纯因子收益率不同。具体的，假设我们有K个因子，某个股票组合对第i个因子的暴露为1，对其他因子的暴露度为0，则这个组合称之为纯因子组合，其收益率称之为纯因子收益率。上次去参加一个深圳的线下活动，有个投资经理就讲到传统的利用因子收益率加权，其实并不是那么合理，因为它的因子收益率可能是在其他风格上的暴露所带来的，因此可以尝试使用纯因子收益率进行加权。那么怎么计算这个纯因子收益率？

通过Fama-MacBeth多元回归，我们可以构造一个纯因子组合。假设有K个因子，股票i在因子k上的暴露度为X(i)^k，记N×k矩阵B为因子暴露矩阵，做横截面回归：

R=Bf+ϵ

可以得到f的ols估计为:

记ω=(B^TB)−1B^T，则ω第k个行向量可以看作某个组合的权重，该组合的收益率就等于第k个因子的回归系数，因为(B^TB)−1B^TB=I，有一个投资经理说那个组合很难计算出来，当然其实公式就这么简单。相信读到这里大家一定明白为什么Barra称回归系数为factor return了。

3.2 行业与风格因子

前面其实我说过了，行业我使用的是申万的一级行业分类，不要问我为什么不用中信的，虽然中信的行业分类中间没有更改过。在模型里面，行业就是哑变量，如果属于这个行业就是1，否则就是0。模型里面还有一个叫国家因子？为什么会有国家因子，国家因子的引入，可以把市场收益率从行业当中分离出来，从而可以更加深入的了解收益与风险的来源，做更加准确的归因分析。但是有一个问题，由于国家因子和行业因子组合放在模型一起，会为回归模型带来一个显然的共线性，为了消除这个现象，我们要使用带约束的最小二乘回归。当然，具体怎么约束的大家可以去参考barra的文档。

风格因子（Style Factor）不是行业这样的离散变量，一些风格因子，本身也是由一些因子合成的（Descriptor）合成的。再把风格因子放到模型之前，需要对风格因子进行处理，包括去极值，处理缺失值，标准化。注意这里的标准化，与前面所说的Alpha因子标准化不太一样，我们减去的是市值加权平均数，为什么这么处理？留给大家去思考。

有没有必要去挖掘新的风格因子？目前来说，可能确实有这方面的需求，特别是有些机构想在不同的股票池做不同的风险模型，这块我想更多的与统计风险模型结合起来。当然，我也会致力提供一个框架的代码，便于去挖掘新的风格因子。

3.3 因子协方差矩阵的估计

这块不能说太多，属于比较核心的东西了。如果感兴趣，可以联系我们的销售。简单来说，在有了因子收益率之后，我们就可以同估计股票的协方差矩阵一样，去估计因子之间的协方差矩阵。那么方法肯定是差不多的，关键在于，有很多细节的调整。例如我们会对收益率做半衰期加权，给近期的观测赋予更高的权重，用来消除不平稳性。当然，半衰期参数的设置就比较考究啦，首先，不同预测期限的模型，半衰期的参数选择肯定是不一样的。这只是第一步，我们还对序列进行NewWey-West调整，用来消除序列的自相关性。在估计完相关系数矩阵之后，还要去估计对角元，还要使用一些调整的方法。具体怎么做，说简单也简单，说复杂也挺复杂。还是要去思考，明白每一步要做的意义。

3.4 特质方差的估计

其实这块和估计因子协方差矩阵的原理来说是类似的，我们也是使用了个股的特质收益序列，用来估计其特质波动。当然，方法肯定不像估计Alpha因子特质波动率那么简单喽。我们也会使用半衰期加权的方式，然后相应的也进行一些调整，用来消除模型外的一些影响因素。

4优化器

4.1 优化模型简介

本来想风险模型多写点的，但是，确实涉及到一些比较核心的东西，所以感兴趣的矿友还是快快先申请我们优矿专业版的试用吧！觉得不错，联系我们的销售，约个路演。我们的优化模型设置如下：

上面的公式给了四个约束：

个股权重约束：这是一个很明显的约束，因为A股市场不允许做空，所以我们个股的权重必须要控制在0到1之间；
权重之和约束：我们假设组合所有股票权重之和为1，也就是满仓；
换手率约束：我们对换手率进行控制，换手率的计算公式为：∑(k)|ω(i,t)−ω(i,t−1)|，注意这个约束带绝对值，求解起来要用特殊的方法；
风险因子约束：我们要控制组合在某个风险因子上的暴露；

当然，还可以添加其他的约束，但本文主要就考虑了这些。那组合优化的意义在于哪呢，其实组合优化的目的在于对投资组合进行精确的控制，包括组合风险暴露、换手率、个股权重上下限、跟踪误差等，降低策略收益的不确定性，但并不一定能提高组合的业绩表现。三点说明：

通过风险因子矩阵X可以得到股票之间的协方差矩阵；
股票的alpha的估计可以使用回归的方法。本文目前只考虑线性规划，所以忽略了二次项，目标函数为最大化组合的Alpha，假设股票的收益率与因子的zscore得分是个线性的关系，因此目标函数直接可以写成最大化股票的zscore得分。当然，正确的做法是要将把多因子得分转换成个股预测收益率，需要做横截面回归；
组合优化可能并不能提高收益，更多的是控制组合的波动，或者做一个组合，用来满足一些特殊的需求；