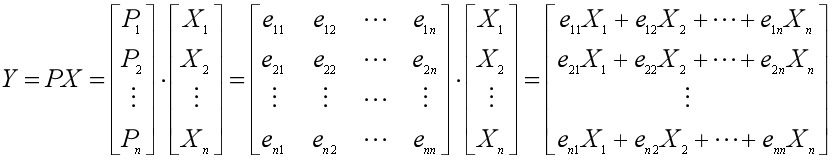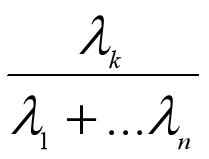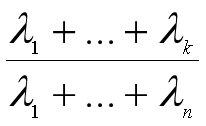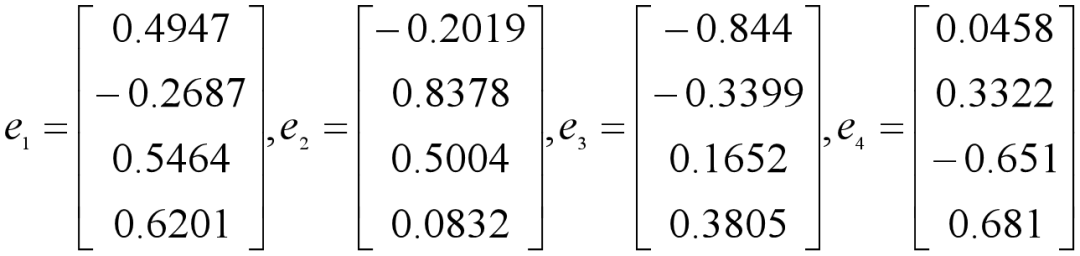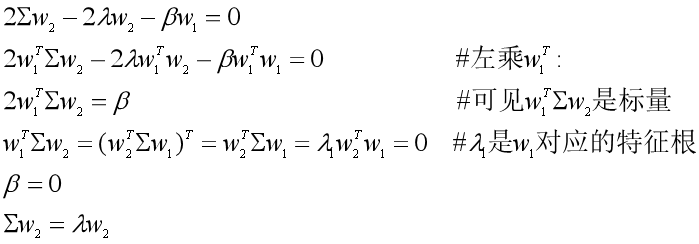【主成分分析法】NLPer的断舍离（下篇）

一：内容预告

上一篇文章介绍了主成分分析法（PCA）的基本思想、主成分矩阵的计算和主成分的选择标准。

这篇文章为主成分分析法的下篇，主要关注以下内容：

• 主成分的方差贡献率

• 基于投影方差最大化的数学推导

二：主成分的方差贡献率

我们拆细了看各主成分是怎么得到的。

主成分可以由协方差矩阵的单位特征向量和原始变量矩阵进行线性组合得到。

P₁就是由，X的协方差矩阵最大特征根，λ₁的单位特征向量e₁转置而成（列向量变为行向量），于是第一主成分就是：

第一主成分的方差是最大的。

第二主成分满足：和第一主成分正交；在剩余的其他主成分中，方差最大。

第二主成分的表达式为：

同理，第k个主成分的表达式为：

我们知道，可以用主成分的方差来衡量其所能解释的数据集的大小，而主成分的方差就是原数据集X的协方差矩阵的特征值λ，所以第k个主成分的方差就是λ_k。

我们来定义一个指标，叫做主成分Y_k的方差贡献率，它是第k个主成分的方差占总方差的比例：

那么前k个主成分的方差累计贡献率为：

如果前k个主成分的方差累计贡献率超过了85%，那么说明用前k个主成分去代替原来的n个变量后，不能解释的方差不足15%，没有损失太多信息。

于是我们可以把n个变量减少为k个变量，达到降维的目的。

三：计算流程总结

为了推导主成分分析法的线性代数解，上一篇文章铺垫了很多，但推导出的结果却是相当漂亮简洁。

现在我们来总结主成分分析法的计算流程。

假设我们拿到了一份数据集，有m个样本，每个样本由n个特征（变量）来描述，那么我们可以按照以下的步骤进行降维：

1、将数据集中的每个样本作为列向量，按列排成一个n行m列的矩阵；

2、将矩阵的每一个行向量（每个变量）都减去该行向量的均值，使新行向量的均值为0，得到新的数据集矩阵X；

3、求X的协方差矩阵，并求出协方差矩阵的特征值λ和单位特征向量e；

4、按照特征值从大到小的顺序，将单位特征向量排列成矩阵，得到转换矩阵P，并按PX计算出主成分矩阵；

5、用特征值计算方差贡献率和方差累计贡献率，取方差累计贡献率超过85%的前k个主成分，或者想降至特定的k维，直接取前k个主成分。

四：主成分计算案例

为了 更好 地掌握主成分分析法 ，我们来看一个例子。

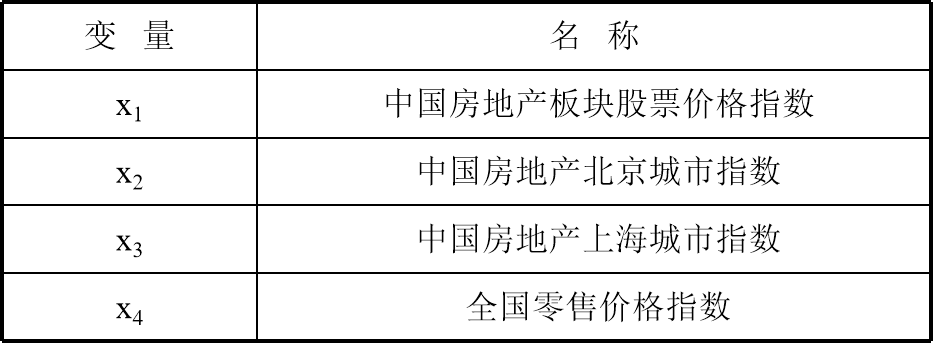
假设我们想研究房价与某些指数之间的关系，设定了4个变量，如下表所示。

样本数据取自1997年1月～2000年6月的统计资料，时间跨度为42个月，因此样本容量为m=42，为了简单起见，数据就不展示了。

第一步：计算数据集的协方差矩阵

将每个样本作为列向量构成一个矩阵，并对矩阵的每一个行向量进行0均值化，得到了4行42列的数据集矩阵X。

我们直接由X得到其协方差矩阵：

第二步：计算协方差矩阵的特征值和单位特征向量

我们用numpy来计算，代码如下：

import numpy as np
from numpy import linalg 

""" 1: 协方差矩阵 """
C = [[1,-0.339,0.444,0.525],
     [-0.339,1,0.076,-0.374],
     [0.444,0.076,1,0.853],
     [0.525,-0.374,0.853,1]]

""" 2: 计算特征值和特征向量 """
value,vector = linalg.eig(C)
print('特征值为：',np.round(value,4),'\n')
for i in range(4):
    print('特征值',np.round(value[i],4),'对应的特征向量为:\n',np.round(vector[:,i].T,4),'\n')

""" 3: 求每一列的L2范数,如果都是1，则已经单位化了 """  
print('特征向量已经是单位特征向量了：',linalg.norm(vector,ord=2,axis=0))

输出结果为：

特征值为： [2.3326 1.0899 0.5399 0.0376] 

特征值 2.3326 对应的特征向量为:
 [ 0.4947 -0.2687  0.5464  0.6201] 

特征值 1.0899 对应的特征向量为:
 [-0.2019  0.8378  0.5004  0.0832] 

特征值 0.5399 对应的特征向量为:
 [-0.844  -0.3399  0.1652  0.3805] 

特征值 0.0376 对应的特征向量为:
 [ 0.0458  0.3322 -0.651   0.681 ] 

特征向量已经是单位特征向量了： [1. 1. 1. 1.]

得到特征值是λ₁=2.3326 ，λ₂=1.0899 ，λ₃=0.5399 ，λ₄=0.0376，已经是从大到小排列好的了。

特征向量已经是单位特征向量了。

第三步：得到转换矩阵P和主成分矩阵Y

我们得到第一个主成分如下，也就是用最大特征值的特征向量对原始变量进行线性组合。

其他三个主成分可以类似得到。

第四步：计算方差贡献率和累计方差贡献率，选择k个主成分

有了协方差矩阵的特征值，计算就非常简单了。

""" 1: 方差贡献率 """
contrib_rate = value/sum(value)
print('方差贡献率为：',np.round(contrib_rate,4))

""" 2: 累计方差贡献率 """
cum_contrib_rate = np.cumsum(contrib_rate)
print('\n累计方差贡献率为：',np.round(cum_contrib_rate,4))

""" 输出结果 """
方差贡献率为： [0.5831 0.2725 0.135  0.0094]
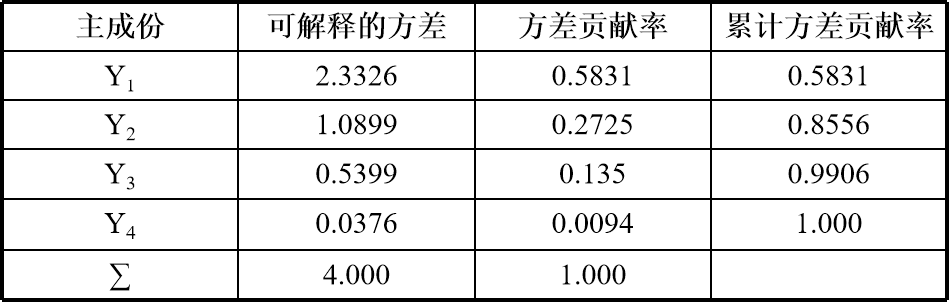
累计方差贡献率为： [0.5831 0.8556 0.9906 1.    ]

得到的结果整理如下。

可以看到第一主成分Y₁和第二主成分Y₂的累计方差贡献率已经达到了85.56%，可以认为，用这两个主成分来代替4个原始变量，也不会造成太多信息损失。

五：基于投影方差最大化的数学推导

下面用其他的方法来推导转换矩阵和主成分的计算公式，可以把主成分的求解问题转换为一个约束条件下求最大值的问题。

假设数据集X有m个样本，每个样本是一个n维的列向量，我们把X整理成n行m列的矩阵：X=(X₁, X₂,..., X_n)^T，且已经对行向量进行了0均值化。

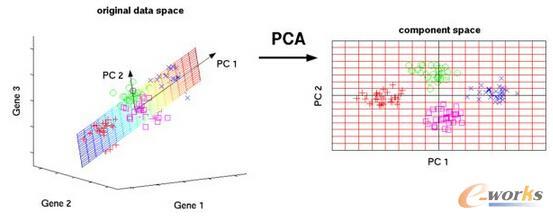
现在我们希望用主成分分析法将n维变量降至k维。

首先进行坐标变换，经过坐标变换后的新坐标系为W=｛w₁, w₂, ...,  w_n｝，其中w_i是标准正交基，W^TW是单位向量。

如果第一主成分Y₁的方向就是w₁这条坐标轴的方向，那么样本投影到w₁上之后会被广泛散布，使得样本之间的差别变得特别明显，也就是投影的方差最大。

设数据集X在w₁上的投影为z₁=w₁^TX，那么问题就成了希望在w₁的L₂范数平方为1的约束条件下，寻找向量w₁，使得投影的方差最大化。

记数据集X的协方差矩阵为Cov(X)=Σ，由z₁乘以其转置，可得投影方差最大化问题为：

写成拉格朗日问题：

对w₁求导并令其为0，得到如下表达式。

Σ是数据集X的协方差矩阵，所以w₁可以看做是协方差矩阵的一个特征值λ的特征向量。

对于以上的式子，等式左右两边都左乘一个w₁^T，得到数据集X在w₁上投影的方差，也就是特征值λ。

由于w₁是第一主成分Y₁所在的坐标轴，那么由方差最大得到λ是最大的特征值。

那么第一主成分怎么求呢？

Y₁=w₁^TX（这里的w₁是特指方差最大化的解）就是了。 

求出了第一主成分，我们可以再求第二主成分。

假设第二主成分Y₂在新坐标轴w₂的方向上，那么Y₂应该是剩余的主成分中，使数据集在w₂上投影的方差最大的那个。

数据集X在w₂上的投影为z₂=w₂^TX，除了满足w₂的L₂范数平方为1的条件外，还需要满足w₂^Tw₁=0，其中w₁是我们已经求出来的。

于是投影方差最大化问题写成拉格朗日问题为：

对w₂求导，经过一系列的推导，我们最终可以得到Σw₂=λw_2。

那么w₂可以看做是协方差矩阵Σ的特征向量，对应的特征值为第二大特征值λ₂，第二主成分为Y₂=w₂^TX。

类似的，其他主成分所在的坐标轴的标准正交基w_i是依次递减的特征值，所对应的单位特征向量。

交流学习，进群备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多： 机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

广告商、博主勿入！