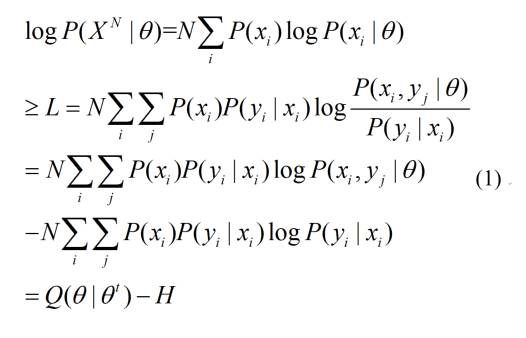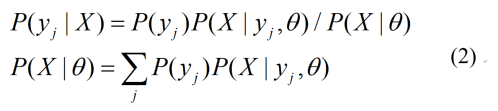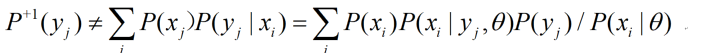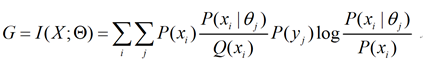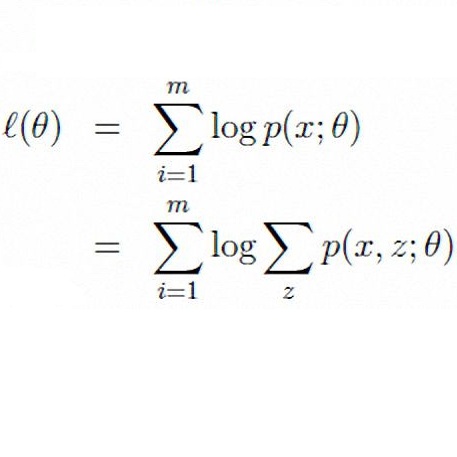EM算法是炼金术吗？

---

  新智元专栏  

作者：鲁晨光

【新智元导读】本文作者解释了EM算法的基本思想和收敛证明存在的问题。作者认为，EM算法虽然在理论上有问题，但是确实炼出金子了。可以说，EM算法正在从“炼金术”向“冶金术”过渡，正视已有问题，寻找更简洁更有说服力理论，可以使“炼金术”成为可靠的“冶金”工具。

人工智能很火，人工智能大神很火。大神们的神器是什么？有人说找到了，就是EM算法。 请看这篇：

EM算法的九层境界：Hinton和Jordan理解的EM算法

但是最近网上引人关注的另一传闻是，一位人工智能论文获奖者在获奖感言中说深度学习方法是炼金术，从而引起大神家族成员反驳。报道见：NIPS机器学习炼金术之争

看到上面两篇，使我想到：EM算法是炼金术吗？

我近两年碰巧在研究用以改进EM算法的新算法：http://survivor99.com/lcg/CM/Recent.html，对EM算法存在的问题比较清楚。我的初步结论是：EM算法虽然在理论上有问题，但是确实炼出金子了。反过来也可以说，虽然EM算法练出金子了，但是收敛很不可靠，流行的解释EM算法的收敛理由更是似是而非。有人使之神秘化，使得它是有炼金术之嫌。论据何在？下面我首先以混合模型为例，简单介绍EM算法，并证明流行的EM算法收敛证明是错的(没说算法是错的)。

假设n个高斯分布函数是：

P(X|θ_j)=Kexp[-(X-c_j)²/(2d_j²)]，j=1，2，…，n

其中K是系数，c_j是中心，d_j是标准差。假设一个数据分布P(X)是两个高斯分布的混合

P(X)=P*(y₁)P(X|θ*₁)+P(y₂)P(X|θ*₂)

其中P*(y₁)，P*(y₂)是真的混合比例，θ*₁和θ*₂表示真的模型参数。我们只知道模型是高斯分布且n=2。现在我们猜测5个参数P(y₁)，c₁，c₂，d₁，d₂。不是6个参数，是因为p(y₂)=1-P(y₁)。根据猜测得到的分布是

Q(X)=P(y₁)P(X|θ₁)+P(y₂)P(X|θ₂)

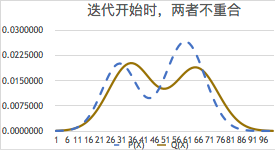
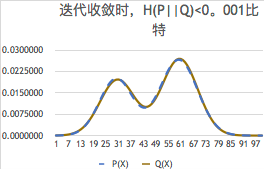
如果Q(X)非常接近P(X)，相对熵或 Kullback-leibler 距离

H(Q||P)=∑_iP(x_i)log[P(x_i)/P(x_i|θ)]

就接近0，比如小于0.001比特，那么就算我们猜对了。参看下图：

 

 

混合模型问题之所以重要，是因为它是限制分布类型而不是分布范围的模糊聚类，是无监督学习的一个典型。

EM算法起源于这篇文章：Dempster, A.P., Laird,  N.M., Rubin,D. B.: Maximum Likelihood from Incomplete Datavia the EM Algorithm. Journal of the Royal Statistical Society, Series B39, 1–38(1977)。通过这个网站http://www.sciencedirect.com/搜索可见，光是标题有EM算法的英文文章就有6.8万篇(有似然度的文章将近76万篇)，可见研究和应用EM算法的人何其多。

Wiki百科上的EM算法介绍见这里：

https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm

一篇中文介绍见这里：

http://www.cnblogs.com/mindpuzzle/archive/2013/04/05/2998746.html

EM算法的基本思想是：

目的是改变预测模型参数求似然度logP(X^N|θ)或logP(X|θ)达最大（N表示有N个样本点，黑体X表示矢量），样本和θ之间的似然度就是负的预测熵（或交叉熵，广义熵的一种）：

H_θ’(X)=∑_iP(x_i)logP(x_i|θ)

其中P(x_i|θ)就是上面的曲线Q(X)上的一个点（X是变量，x_i是常量），即P(x_i|θ)=Q(x_i)。我们用X的概率分布P(X)取代X序列。则EM算法的基本公式如下(下面y就是wiki百科中的z)：

其中θ^t表示M步优化前的θ。这里的Q和上面的Q(X)中的Q含义不同，下面我们用Q(.)表示这里的Q(θ|θ^t)。

从语义信息论(http://survivor99.com/lcg/books/GIT/)看，我们可以得到

[Q(θ|θ^t)-H]/N=H_θ’(X，Y)-H_θ’(Y|X)=-H_θ(X，Y)+H_θ(Y|X)

右边是两个负的广义熵或负的交叉熵，和参数有关。为了讨论方便，后面忽略左边的N。

EM算法分两步：

E-step：写出预测的y_j的条件概率

M-step：最大化Q(θ|θ^t)，也就是最大化负的联合熵H_θ’(X，Y)，或最小化联合交叉熵H_θ(X，Y)。

为什么这样能收敛呢？wiki百科这样说：

1. Expectation-maximization works to improve Q(θ|θt) rather than directly improving log(X|θ). Here is shown that improvements to the former imply improvements to the latter.[13]

这就是说，只要Q(.)达最大，log(X|θ)就达到最大。

2）M-step可以增大Q(.)，E-step也不减少Q(.)，所以反复迭代就能收敛。

这篇证明文章比较出名：Wu, C.F.J.: On the Convergence Properties of the EM Algorithm. Annals of Statistics11, 95–10(1983)。

这等于说，真模型在山顶上，爬山人每一步只上不下就能到达山顶。M步只上，E步不下，所以能到达山顶。

但是，使用EM算法时，往往在预测分布P(X|θ)和实际分布P(X)不重合就停下来了。流行的解释是：那叫局部收敛（其实就是收错了地方）；因为大山周围有一些小山，出发点不对就上到小山顶上了。所以起始点很重要。于是有人专门研究如何通过测试找到较好的出发点，比如随机选多点测试看哪个好。

EM有时虽然能收敛，但是常常收敛很慢。为了提高速度，于是又有很多人提出很多改进办法。其中比较出名的一个就是上面《九层境界》中提到的VBEM算法(详见Neal, R.，Hinton, G.: A view of the EM algorithm that justifies incremental, sparse, and other variants. in: Michael I. Jordan(ed.) Learning in Graphical Models，pp355–368. MITPress，Cambridge，MA(1999))，就是用

F(θ，q)=Q(θ|θ^t)+H(Y)

取代Q(θ|θ^t)(上面忽略了系数N)，不断最大化F(θ，q)(q=P(Y))。在M步最大化F(.)，在E步也最大化F(.)。据说这样收敛更快。但是VBEM的收敛证明是不是一样有问题呢？我的结论是：算法好一些，但是收敛证明问题还是存在。

首先我们看EM算法(包括VBEM算法）的收敛证明错在哪里。

在Shannon信息论中有公式：

H(X，Y)=H(X)+H(Y|X)

由于引进似然函数，Shannon熵变成预测熵或交叉熵，但是基本关系还是成立

H_θ(X，Y)=H_θ(X)+H_θ(Y|X)=-logP(X|θ)+H_θ(Y|X)

写成负熵的形式是：

H’_θ(X，Y)=logP(X|θ)+H’_θ(Y|X)

后面这一项H_θ(Y|X)和Y的熵有关，P(y₁)=P(y₂)=0.5的时候H(Y)最大，负熵就最小，H’_θ(Y|X)也比较小。如果真的比例P*(Y)是接近等概率的，起步时P(y₁)=0.1，P(y₂)=0.9，Y的负熵较大，我们不断最大化H’_θ(X，Y)，就会阻止P(Y)向真比例P*(Y)靠近。这是EM算法收敛慢甚至不收敛的一个原因。这也是为什么VBEM方法要用F(.)取代Q(.)。上式两边加上H(Y)以后就有

H’_θ(X，Y)+H(Y)=logP(X|θ)+H’_θ(Y|X)+H(Y)

H(Y)-H_θ(X，Y)=-H_θ(X)+H(Y)-H_θ(Y|X)

近似得到(后面解释近似)：

-H_θ(X|Y)=-H_θ(X)+I_θ(X;Y)

也就是

F(θ，q)=-H_θ(X|Y)=-H_θ(X)+I_θ(X;Y)(3)

可见，F(θ，q)就是负的后验熵。两边加上P(X)，左边就是预测互信息或语义互信息(我早在1993年的《广义信息论》一书中就提出)：

F(θ，q)+H(X)=H(X)-H_θ(X|Y)=I(X;ϴ)(4)

从上面两个公式可以得到

H(Q||P)=H(X|θ)-H(X)=I_θ(X;Y)-I(X;ϴ)(5)

我们可以粗略理解，相对熵=Shannon互信息-预测互信息。后面我们将介绍这个公式的更加严格形式。

因为H(X)和模型无关，最大化F(.)就是最大化预测互信息，避免误改P(Y)。这样就好理解为什么VBEM比EM好。

但是，F(θ，q)最大化和logP(X|θ)最大化是否总是一致的？结论是否定的。证明很简单：

假设有一个真模型θ*和子模型比例P*(Y)，它们产生P(X)。同时相应的Shannon联合熵是H*(X，Y)，X的后验熵是H*(X|Y)，互信息是I*(X;Y)。那么改变X和Y的概率分布，上面三个量都会变。

我们猜测的时候，如果联合概率分布P(Y，X|θ)比P*(X，Y)更加集中，负熵log(X，Y|θ)=H’_θ(X，Y)就会大于真模型的负熵-H*(X，Y)，继续增大H’_θ(X，Y)就会南辕北辙。

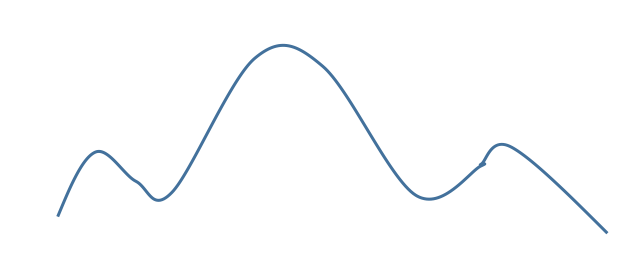
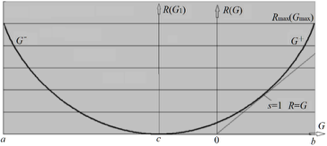
比如，下图例子中，第一轮优化参数前就可能有H’_θ(X，Y)>-H*(X，Y)。它对于EM算法收敛证明来说就是反例。图中R=I(X;Y)，R*=I*(X;Y)。其中真实的Q*(.)和互信息I*(X;Y)比较小。

 

这个例子中迭代用的是信道匹配算法，和VBEM算法比，主要差别是，在E步把继续增大F(.)改为调整P(Y)。其中红线就是EM算法中Q(θ|θ^t)的变化轨迹，第一个E步之后，Q(.)就大于真模型的Q*(.)。如果起始参数是随机的，那么它可能导致Q(.)出现在红线的任何位置，从而大于Q*(.)。

F(.)有类似情况，它和预测互信息(图示是G)走势完全一致，在每个E步是下降的。原来影响交叉熵有三个因素：

1)预测的分布和样本的分布是否符合，如果更符合，负熵Q(.)和F(.)就更大；

2)X和Y的分布是否集中，如果更集中负熵就更大；

3)X和Y是否相关，如果更相关负熵就更大。

流行的收敛证明只考虑了第一条。

到此有人会问，如果终点不在山顶上，起点很可能高于终点，那么为什么EM算法在大多数情况下是收敛的？

回答是：EM算法收敛证明中第二条，Q(.)只增不减也错了！原来在E步，Q(.)和F(.)是可能减小的！一般情况下都会使Q(.)向真模型的Q*=-H*(X，Y)靠拢，使F(.)向-H*(X|Y)靠拢。如果调整P(Y)，收敛就更加可靠，EM算法就变为CM算法。

下面提供CM算法的粗略数学证明。

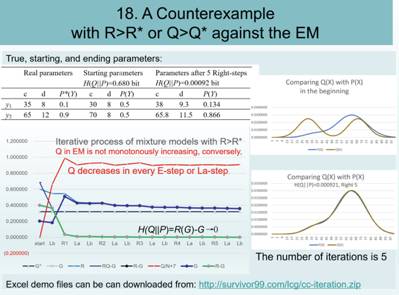
先看为什么需要调整P(Y)。在E步的公式(2)(计算Shannon信道的公式)中，P(yj|X)和P(X)及四个参数可能不匹配，导致

 

那样，上面计算出的Shannon信道就是一个不称职的Shannon信道。调整方法很简单，就是不断用左边的P⁺¹(y_j)代替右边的P(y_j)，直到两者相等。

下面介绍用信道匹配算法(CM算法)用到的公式：

上面第一行公式就是公式(5)的更加严格形式。其中用到子模型θ_j，P(X|θ_j) 就等于前面方法中的P(X|y_j，θ)。R_Q就近似于前面方法中I_θ(X;Y)。为什么说近似呢，因为这里用到Y的广义熵或交叉熵 H(Y⁺¹)=-∑_jP⁺¹(y_j)logP(y_j) 和相对熵H(Y⁺¹||Y)。联合熵减去这个熵才是预测后验熵。而在VBEM方法中，增加的H(Y)是Shannon熵。

有了上面公式(6)，我们就可以采用下面三步减小相对熵H(Q||P)——保证每一步都是减小的：

I：写出Shannon信道表达式，等于EM算法中的E步;

II：调整P(Y)，使得P(Y+1)=P(Y);如果H(Q||P)<0.001，结束。

III:改变参数最大化语义互信息G。转到I。

详细讨论见这里：http://survivor99.com/lcg/CM.html

如果EM算法在M步先调整P(Y)，固定P(Y)再优化参数，EM算法就和CM算法相同。如果在VBEM算法中添加的H(Y)改为交叉熵，E步调整P(Y)而不是最大化F(.)，VBEM算法就和CM算法相同。

从语义互信息公式看

迭代就是轮流改变log左边(I和II)和右边(III)。改变右边是语义信道匹配Shannon信道，改变左边是Shannon信道匹配语义信道。所以该算法叫信道匹配(Channels’Matching)算法或CM算法(保留EM中的M)。我们也可以说CM算法是EM算法的改进版本。但是基本思想是不同的。CM算法也没用到Jensen不等式。

为什么CM算法会使Q(X)会收敛到P(X)呢？相对熵会不会表现为很多山洼，有高有低，我们不巧，落到一个较高的山洼里呢？

这要从Shannon的信息率失真理论谈起。Shannon在1948年发表经典文章《通信的数学理论之》，11年之后，他提出信息率失真函数R(D)——就是给定平均损失上限D求互信息I(X;Y)最小值R(D)。我在1993年的《广义信息论》中把它改造为R(G)函数。G是广义互信息或语义互信息(也就是平均log标准似然度)的下限。R(G)是给定G时的Shannon互信息I(X;Y)的最小值。可以证明，所有R(G)函数都是碗状的。R(D)函数像是半个碗，也是凹的。证明G是碗状的很简单，因为R(D)函数处处是凹的(已有结论)，R(G)函数是它的自然扩展，也是处处是凹的。

进一步结论：R(G)-G也是处处是凹的。所以山洼只有一个。求相对熵最小，就是求R(G)-G最小，就是找R=G的点，也就是上图中45度斜线和碗状曲线相切的点。

像E步那样，用公式(2)求Shannon信道，并调整P(Y)，就能得到R(G)。原来求信息率失真函数也用到迭代算法，也用到和公式(2)类似的公式。EM和VBEM算法之所以慢，除了因为没有调整P(Y)，还和指导思想有关。因为认为增大负熵就能达到目的，所以设置初始参数时就想把负熵弄得小一点，比如把两个标准差d1和d2设得大一点，防止漏掉真模型。但是在计算试验中我发现，有时候选择较小的偏差，收敛反而更快。从文献数字和我的计算实验看，CM算法迭代5次收敛比较常见，而EM算法(包括改进的)达到收敛的迭代次数大多超过10次。

诚然，CM算法也不是完美无缺的。在少数极端情况下(比如两个分布重叠较多，两个分量比例相差较大时)，初始值选择不当收敛也很慢。结合已有的EM算法研究中关于初始参数的研究成果，应该还能改进。

我上面只是证明了流行的EM算法收敛证明是错的，是否还有其他对的证明？我不能肯定。北大的马尽文教授是EM算法专家，做过很多推广和应用。他说有，我很期待。我以为如果有，可能和我的证明异途同归。我和VBEM的第一作者Neal教授通过信，他说要是E步减小Q(.)或F(.)，那就太震动了。看来他一直相信流行的负熵只增不减证明。

现在回到“炼金术”话题。

实际上，把深度学习和炼金术联系起来的AliRahimi教授演讲标题是：

《从“炼金术”到“电力”的机器学习》，他并没有否定深度学习，只是说要加强理论研究，也不排除先有实践再有理论。

根据上面分析，可以说EM算法正在从“炼金术”向“冶金术”过渡。如过它在理论上停滞不前，如果我们把它神话，它就真像是炼金术了。反之，正视已有问题，寻找更简洁更有说服力理论，才能使“炼金术”成为可靠“冶金”工具。

作者简介：

鲁晨光，男，南京航空航天大学毕业(77级). 当过长沙市青年学术带头人，赴加拿访问学者，北师大数学系访问学者（汪培庄教授指导）…研究兴趣是：语义信息论，统计学习，色觉的数学和哲学, 美学和进化论，投资组合。专著有：《广义信息论》，《投资组合的熵理论和信息价值》，《色觉奥妙和哲学基本问题》，《美感奥妙和需求进化》。于《光学学报》,《机器人》，《通信学报》,《现代哲学》,《Int. J. of General System》等杂志上发表论文多篇。最近主要工作是把语义信息论用到统计学习，用以解决最大似然估计，贝叶斯推理， 多标签分类， 混合模型等问题。个人网站：http://survivor99.com/lcg/ 信箱：lcguang@foxmail.com。

---