方程组的几何解释 [MIT线代第一课pdf下载]

攻读鉴于之前MIT的线代笔记没有跟新完和很多童鞋希望pdf版本下载学习，这里我把相关资源放到github上并重新更新完，希望对大家学习有所帮助。

pdf下载地址与Github地址:

https://github.com/yizhen20133868/MIT-Linear-Algebra-Notes

如有帮助，欢迎大家给个Star！！

该笔记总结了我们在学习MIT线性代数课程的学习经验和过程。

课程顺序是按照麻省理工公开课的 Linear Algebra. 记录的学习笔记。

本笔记作者介绍：
丁坤博 东北大学本科生，推免至北京大学攻读硕士
覃立波 哈尔滨工业大学SCIR实验室在读博士生，导师车万翔老师

一、知识概要

本节开始，我们一起来学习线性代数的有关知识，首节我们从解方程谈起，学 习线性代数的应用之一就是求解复杂方程问题，本节核心之一即为从行图像与列 图像的角度解方程。

二．方程组的几何解释基础

2.1 二维的行图像

我们首先通过一个例子来从行图像角度求解方程：

系数矩阵(A)：将方程系数按行提取出来，构成一个矩阵

未知向量(x)：将方程未知数提取出来，按列构成一个向量。

向量(b) ：将等号右侧结果按列提取，构成一个向量

接下来我们通过行图像来求解这个方程：

所谓行图像，就是在系数矩阵上，一次取一行构成方程，在坐标系上作图。

和我们在初等数学中学习的作图求解方程的过程无异。

2.2 二维的列图像

接下来我们使用列图像求解此方程：

即寻找合适的 x，y 使得 x 倍的(2,-1) + y 倍的(-1,2)得到最终的向量(0,3)。在很 明显能看出来，1 倍(2,-1) + 2 倍(-1,2)即满足条件。反映在图像上，明显结果正确。

三.方程组的几何解释推广

3.1 高维行图像

如果绘制行图像，很明显这是一个三个平面相交得到一点，我们想直接看出 这个点的性质可谓是难上加难，比较靠谱的思路是先联立其中两个平面，使其相 交于一条直线，在研究这条直线与平面相交于哪个点，最后得到点坐标即为方程 的解。

这个求解过程对于三维来说或许还算合理，那四维呢？五维甚至更高维数 呢？直观上很难直接绘制更高维数的图像，这种行图像受到的限制也越来越多。

3.2 高维列图像

左侧是线性组合，右侧是合适的线性组合组成的结果，这样一来思路就清晰多 了，“寻找线性组合”成为了解题关键。

很明显这道题是一个特例，我们只需要取 x = 0，y = 0，z = 1。就得到了结 果，这在行图像之中并不明显。

当然，之所以我们更推荐使用列图像求解方程， 是因为这是一种更系统的求解方法，即寻找线性组合，而不用绘制每个行方程的 图像之后寻找那个很难看出来的点。

另外一个优势在于，如果我们改变最后的结果 b，例如本题中，

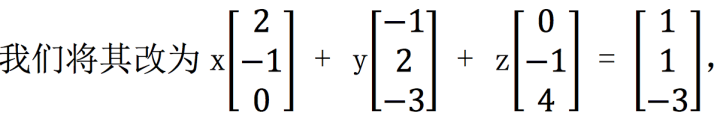
那么我们 2 −1 1 0 −3 4 −3 就重新寻找一个线性组合就够了，但是如果我们使用的是行图像呢？那意味着我 们要完全重画三个平面图像，就简便性来讲，两种方法高下立判。

另外，还要注意的一点是对任意的 b 是不是都能求解 Ax = b 这个矩阵方程呢？也就是对 3*3 的系数矩阵 A，其列的线性组合是不是都可以覆盖整个三维空间呢？对于我们举的这个例子来说，一定可以，还有我们上面 2*2 的那个例子，也可以 覆盖整个平面，但是有一些矩阵就是不行的，比如三个列向量本身就构成了一个 平面，那么这样的三个向量组合成的向量只能活动在这个平面上，肯定无法覆盖 2 −1 1 一个三维空间，

这三个向量就构

3.3 矩阵乘法

四、学习感悟

这部分内容是对线性代数概念的初涉，从解方程谈起，引进列空间的概念，可 以发现从列空间角度将求解方程变化为求列向量的线性组合，这个方式更加科学。介绍了矩阵乘法，这部分内容重在理解。

希望对大家有帮助~

下载如下资料可以访问项目地址：

https://github.com/yizhen20133868/MIT-Linear-Algebra-Notes

本文转载自公众号：机器学习算法与自然语言处理，作者：丁坤博、覃立波

推荐阅读：

2021 校招算法岗， 劝退还是继续

一文读懂最强中文NLP预训练模型ERNIE

神经网络硬核入门-反向传播(BP)算法