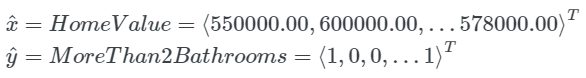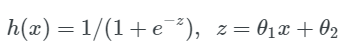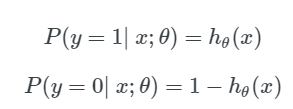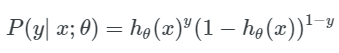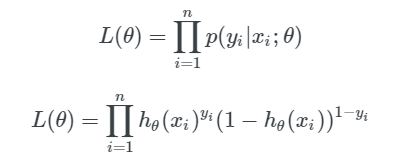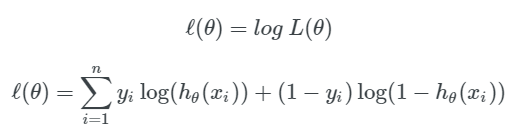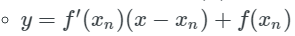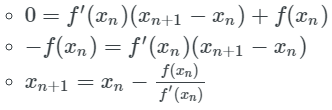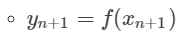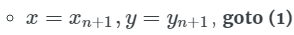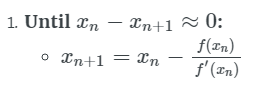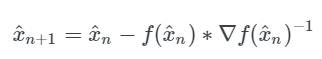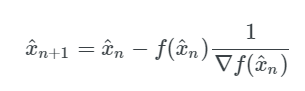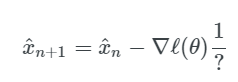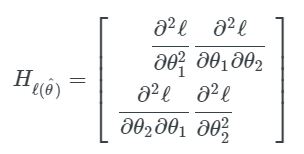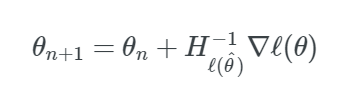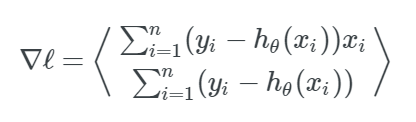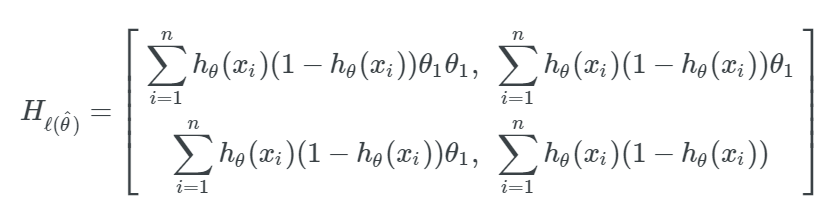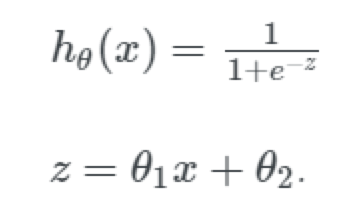如何通过牛顿法解决Logistic回归问题
| 全文共8033字,建议阅读时长5分钟 |
内容来源:TLP
转载公众号:机器之心
微信号:almosthuman2014
参与:Nurhachu Null、黄小天
本文介绍了牛顿法(Newton's Method),以及如何用它来解决 logistic 回归。logistic 回归引入了伯努利分布(Bernoulli distribution)中的对数似然概念,并涉及到了一个称作 sigmoid 函数的简单变换。本文还介绍了海森矩阵(这是一个关于二阶偏微分的方阵),并给出了如何将海森矩阵与梯度结合起来实现牛顿法。
与最初的那篇介绍线性回归和梯度的文章相似,为了理解我们的数学思想是如何转换成在二元分类问题中的解决方案的实现,我们也会用 Python 语言以一种可视化、数学化的方式来探索牛顿法:如何解决 logistic 回归问题。
读者需知的先验知识:
1. 微分和链式法则(微积分)
2. 偏微分与梯度(多元微积分)
3. 基本向量运算(线性代数)
4. NumPy 的基本理解
5. 独立概率的基本理解
数据
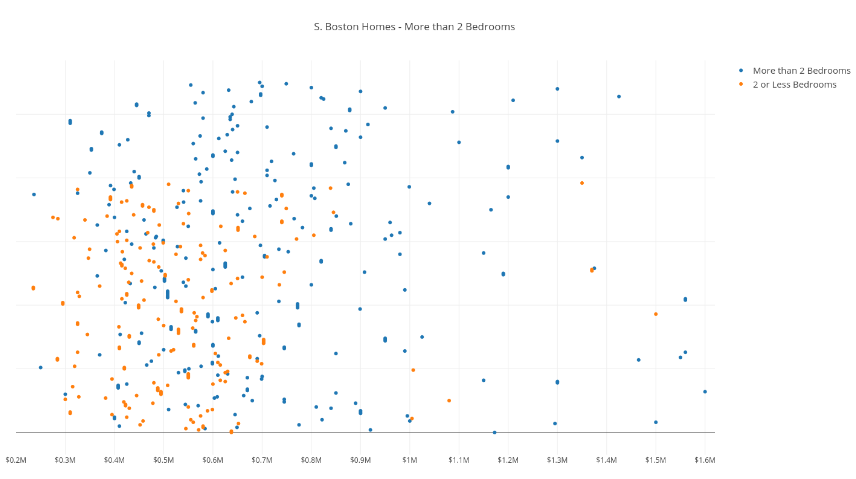
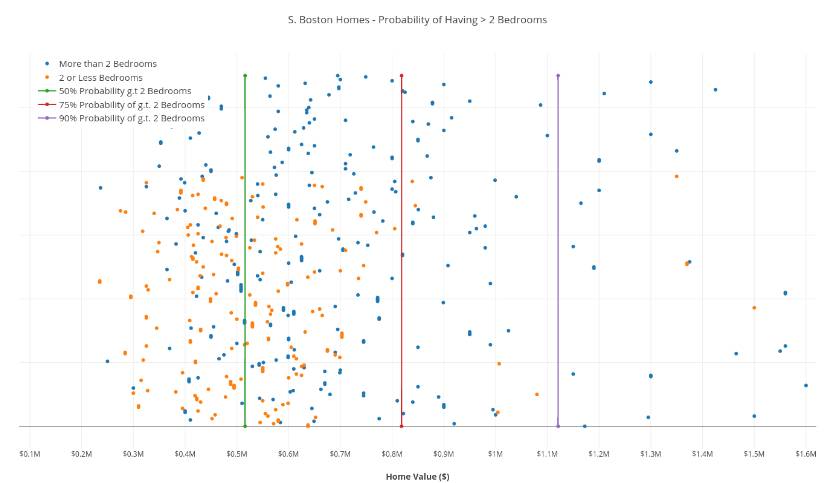
我们的数据集来自南波士顿的房地产,包括每套房子的价格以及一个表明这套房子是否具有两个浴室的布尔值。
x 是房产价格的向量,y 是房产是否具有两个浴室的向量
蓝色点代表具有两个以上浴室的房产,橙色点代表具有 2 个或者少于两个浴室的房产,横坐标是房产价格。
模型
我们将会学习一个 logistic 回归模型,它将会作为一个二元分类器来预测一套给定价格(单位是美元)的房产是否具有两间或者两间以上的浴室。
我们仍然需要解决一个关于权重和特征的线性组合,但是我们需要结合一个平滑的、而且值域在 [0,1] 之间的函数来对这个线性组合做一个变换(因为我们需要将线性组合与一个二值输出 0 或者 1 映射起来。)
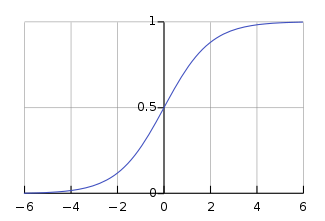
logistic 函数,也就是 sigmoid 函数,能够完成所有这些事情,函数表达式如下:
注意:为了让函数具有更多的灵活性,我们在指数项上添加了 θ2 作为一个截距;我们只有一维的数据,即 house_value,但是我们要解决一个二维的模型。
在线性回归问题中我们定义了我们的平方和目标函数,与这种方法类似,我们想使用假设函数 h(x),并且定义似然函数(likelihood function)来最大化目标函数,拟合出我们的参数。下面是相关内容的数学分析:
数学:定义似然函数
首先,我们要定义一个概率质量函数(Probability Mass Function):
注意:第一个式子中,左侧代表得失:在给定的参数 θ 和特征向量 x 的情况下,结果为 1 的概率,我们的假设函数 h_θ(x)来计算这个概率。两个表达式可以结合成一个,如下所示:
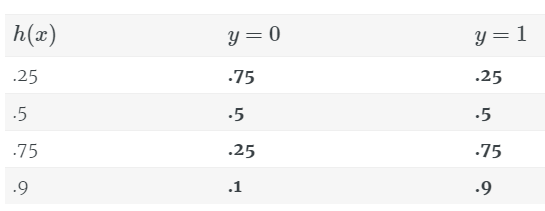
下表展示了使用假设函数得到的错误结果是如何通过生成一个较小的值来接受惩罚的(例如,h(x)=.25,y=1h(x)=.25,y=1)。这也有助于理解我们如何把两个式子合并成一个。
自然而然,我们想把上述正确预测结果的值最大化,这恰好就是我们的似然函数。
我喜欢将似然函数描述成「在给定 y 值,给定对应的特征向量 x^ 的情况下,我们的模型正确地预测结果的似然度。」然而,区分概率和似然值非常重要。
现在我们将似然函数扩展到训练集中的所有数据上。我们将每一个单独的似然值乘起来,以得到我们的模型在训练数据上准确地预测 y 值的似然值的连乘。如下所示:
可以看到我们把 n 个似然值乘了起来(每个似然值都小于 1.0),其中 n 是训练样本的数量,我们最后得到的结果的数量级是 10^(-n)。这是不好的一点!最终可能会由于数值太小而用尽计算机的精度,Python 会把特别小的浮点数按照 0 来处理。
我们的解决办法就是给似然函数取对数,如下所示:
注意:log(x*y) = log(x)+log(y);log(x^n) = n*log(x)。这是我们的假设函数的对数似然值。
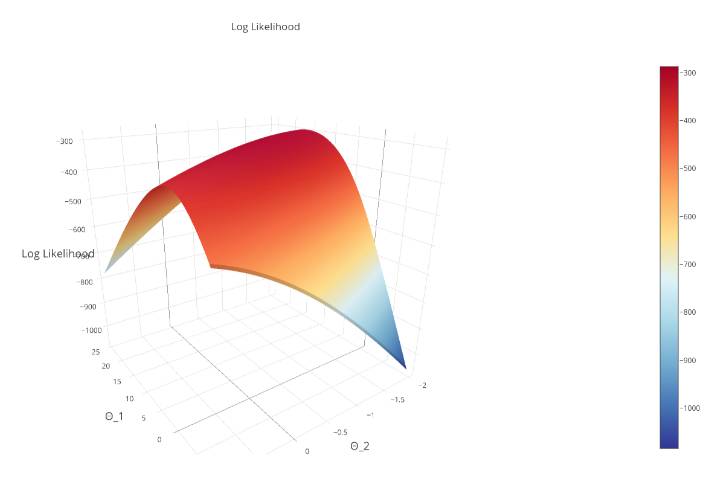
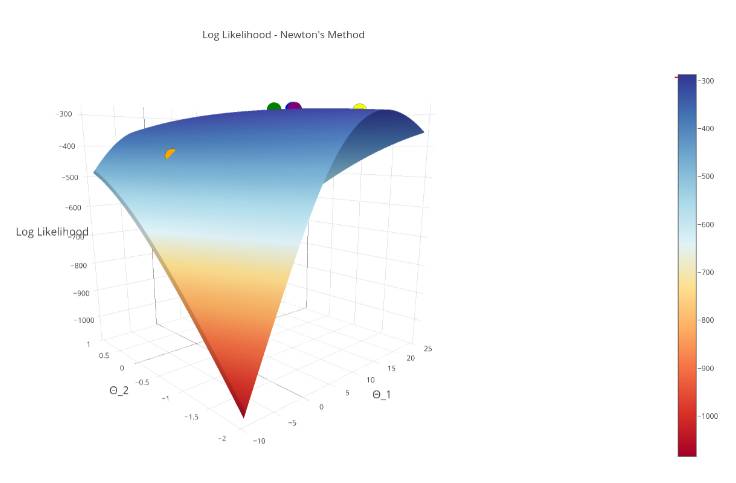
记住,我们的假设函数通过生成一个很小的值来惩罚错误的预测,所以我们要将对数似然函数最大化。对数似然函数的曲线如下图所示:
注意:通过对函数取对数,我们便得到了对数似然值(log-likelihood),我们确保我们的目标函数是严格的凸函数(这是一项附加条件),这意味着它有一个全局最大值。
数学:单变量的牛顿法
在我们最大化对数似然函数之前,需要介绍一下牛顿法。
牛顿法是迭代式的方程求解方法;它是用来求解多项式函数的根的方法。在简单的、单变量的情况下,牛顿法可以通过以下步骤来实现;
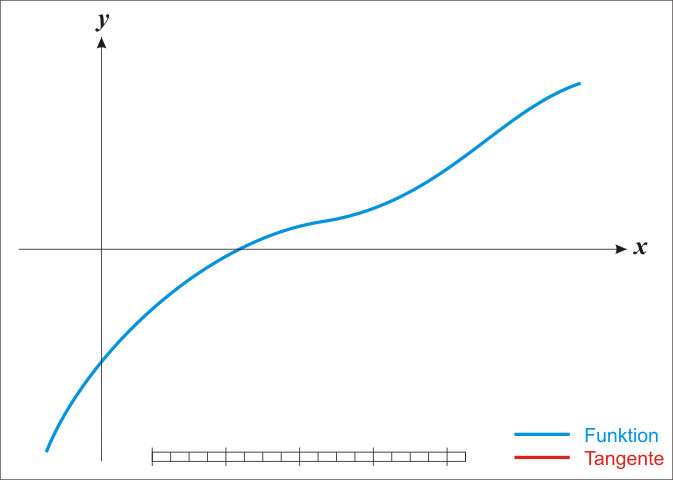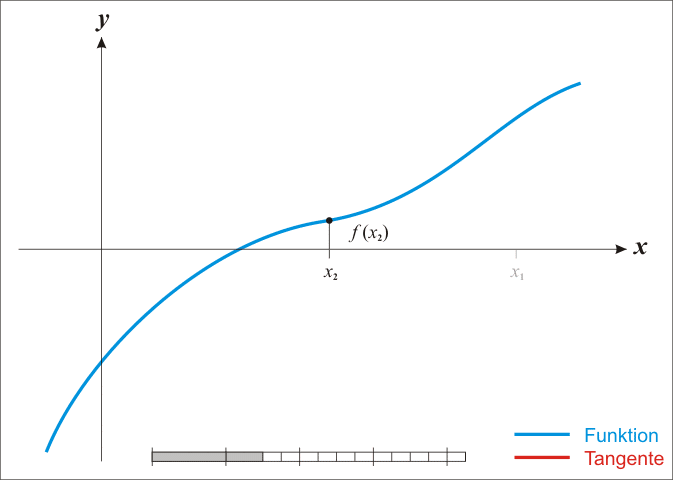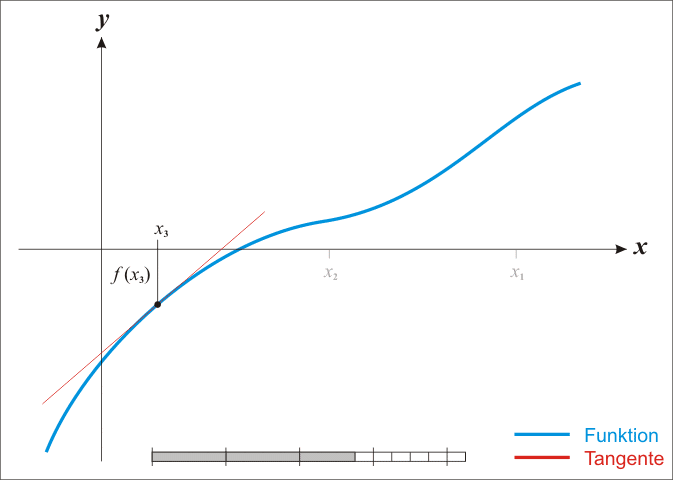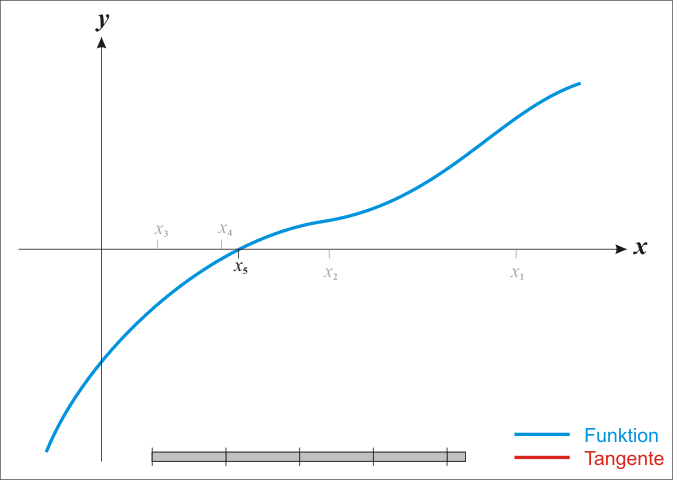
求取函数 f(x) 在点 (xn,yn) 处的切线:
求取点 x_n+1, 处的切线的在 x 轴的截距:
求出 x 截距处的 y 值
如果 yn+1−yn≈0:返回 yn+1,因为我们的结果已经收敛了!
否则,更新点 (xn,yn),继续迭代:
下面的动图有助于我们可视化这个方法:
如果你能够更详细地理解上述算法,你将看到这个可以归结为:
任何一位通过高中数学考试的人都能够理解上面的内容。但是我们如何将其推广到多变量的「n 维」情况中呢?
数学:N 维问题中的牛顿法
说到 n 维情况,我们用一个叫做梯度的偏微分向量来代替单变量微分。
如果这个概念对你而言有些模糊,那么请复习一下梯度的知识。
所以在多变量的形式中,我们的更新规则变成了参数 x^ 的向量减去 f(x^),如下所示:
注意: f(xn)f′(xn) 中的 f′(xn) 变成了 ∇f(x^n)^(−1),因为我们将标量 f(xn) 推广到了多变量的情况下,将它变成了梯度的倒数 ∇f(x^n)^(−1)。
数学:用牛顿法最大化对数似然函数
我们要最大化假设函数 hθ(x) 的对数似然值ℓ(θ)。
为了最大化我们的函数,我们要找到函数 f ℓ(θ) 的偏微分,并且将它设为 0,然后从中求出 θ1 和 θ2,来得到微分的临界点。这个临界点就是对数似然函数的最大值点。
注意:因为对数似然函数是严格的凸函数,所以我们会有一个全局最大值。这意味着我们只有一个临界点,所以通过上述方法得到的解就是我们的唯一解。
这应该听起来很熟悉。我们寻求使偏微分为 0 的 θ1 和 θ2。我们找到了梯度向量的根。我们可以使用牛顿法来做这件事!回想一下牛顿法的更新步骤:
我们可以用梯度来代替 f(x^n),这样就得到了:
那么上面的「?」指的是什么呢?直觉告诉我们,我们需要对梯度向量求导,就像我们之前对 f(x^n) 所做的微分一样。
开始进入海森矩阵(The Hessian)。
数学:海森矩阵
从关于多元微分的预备知识中可以得知,我们应该知道去求解一个函数的「二阶」导数,我们针对每一个参数再给每个一阶偏导数求偏导数。如果我们有 n 个参数,那么我们就会有 n^2 个二阶偏导数。
结果就是,海森矩阵是一个 n*n 的二阶偏导方阵。
在我们的情况中,一共有两个参数 (θ1,θ2),因此我们的海森矩阵形式如下:
数学:将所有的放在一起
将海森矩阵替换在牛顿法的更新步骤中,我们得到了如下所示的内容:
注意:我们取了海森矩阵的逆矩阵,而不是它的倒数,因为它是一个矩阵。
为了简单起见,这篇文章省略了对梯度和海森矩阵进行求导的实际过程。要理解后面的求导过程可以参考下面的资源:
1. 我们的对数似然函数的梯度的导数(Derivation of the Gradient of our Log-Likelihood), 吴恩达课程笔记 17-18 页
2. 海森矩阵的求解其实相当直接,如果你曾经计算过梯度,你会在吴恩达课件笔记中「对 sigmoid 函数求导 g′(z)」那一部分看到。
ℓ(θ) 的梯度是:
ℓ(θ) 的海森矩阵是:
其中:
实现牛顿法
我们从定义假设函数开始,它就是 sigmoid 函数:
def sigmoid(x, Θ_1, Θ_2):
z = (Θ_1*x + Θ_2).astype("float_")
return 1.0 / (1.0 + np.exp(-z))
然后定义我们的对数似然函数 ℓ(θ):
def log_likelihood(x, y, Θ_1, Θ_2):
sigmoid_probs = sigmoid(x, Θ_1, Θ_2)
return np.sum(y * np.log(sigmoid_probs)
+ (1 - y) * np.log(1 - sigmoid_probs))
最后,我们实现对对数似然函数的梯度求解和海森矩阵求解:
def gradient(x, y, Θ_1, Θ_2):
sigmoid_probs = sigmoid(x, Θ_1, Θ_2)
return np.array([[np.sum((y - sigmoid_probs) * x),
np.sum((y - sigmoid_probs) * 1)]])
def hessian(x, y, Θ_1, Θ_2):
sigmoid_probs = sigmoid(x, Θ_1, Θ_2)
d1 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * x * x)
d2 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * x * 1)
d3 = np.sum((sigmoid_probs * (1 - sigmoid_probs)) * 1 * 1)
H = np.array([[d1, d2],[d2, d3]])
return H
实现了上述 4 个数学过程之后,我们就使用牛顿法创建我们的外部 while 循环,直到结果在最大值的地方达到收敛。
def newtons_method(x, y):
"""
:param x (np.array(float)): Vector of Boston House Values in dollars
:param y (np.array(boolean)): Vector of Bools indicting if house has > 2 bedrooms:
:returns: np.array of logreg's parameters after convergence, [Θ_1, Θ_2]
"""
# Initialize log_likelihood & parameters
Θ_1 = 15.1
Θ_2 = -.4 # The intercept term
Δl = np.Infinity
l = log_likelihood(x, y, Θ_1, Θ_2)
# Convergence Conditions
δ = .0000000001
max_iterations = 15
i = 0
while abs(Δl) > δ and i < max_iterations:
i += 1
g = gradient(x, y, Θ_1, Θ_2)
hess = hessian(x, y, Θ_1, Θ_2)
H_inv = np.linalg.inv(hess)
# @ is syntactic sugar for np.dot(H_inv, g.T)¹
Δ = H_inv @ g.T
ΔΘ_1 = Δ[0][0]
ΔΘ_2 = Δ[1][0]
# Perform our update step
Θ_1 += ΔΘ_1
Θ_2 += ΔΘ_2
# Update the log-likelihood at each iteration
l_new = log_likelihood(x, y, Θ_1, Θ_2)
Δl = l - l_new
l = l_new
return np.array([Θ_1, Θ_2])
可视化牛顿法
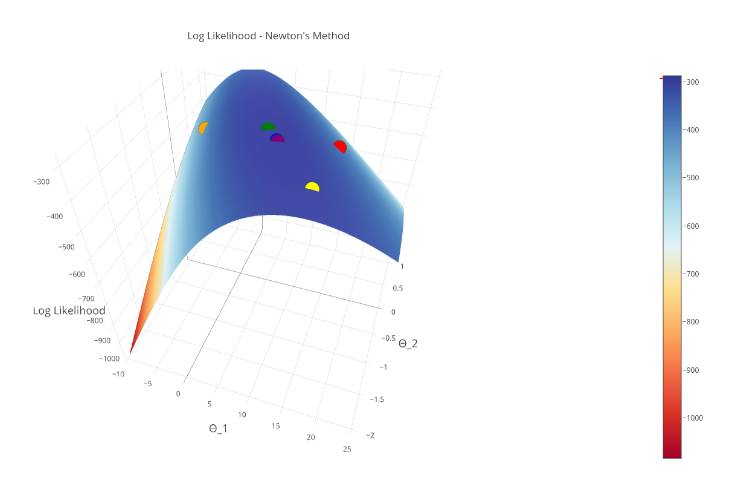
让我们看一下当我们把在对数似然曲面上使用牛顿法的每一次迭代都画出来的时候会发生什么?
注意:第一次迭代是红色的,第二次是橙色的...... 最后一次迭代是紫色的。
在这幅图中,可以确认我们的「紫色区就是最大值」,我们成功地收敛了!
可视化我们的解
通常,为了可视化一个 1 维数据集,你会把所有的点在数字轴上画出来,并在数字轴的某处设置一个界限。然而这里的问题是所有的数据点都被混在一起了。
所以,我们在 x 轴将它们展开,并将这些点用颜色来标记。我们也画出了 3 条界线来区分房产的百分比——正如图例解释的一样。
结论
我们介绍了一些新主题,包括海森矩阵、对数似然以及 sigmoid 函数。将这些方法结合在一起,我们就能实现用牛顿法来解决 logistic 回归问题。
尽管这些概念促使形成了实现我们的解决方案的具体化的基础,但是我们仍然需要注意那些能够导致牛顿法发散的地方,这些内容超出了本文所要讨论的范围,但是你可以阅读更多发散资料。
有缘的人终会相聚,慕客君想了想,要是不分享出来,怕我们会擦肩而过~
《【调查问卷】“屏幕时代,视觉面积与学习效率的关系“——你看对了吗?》
本文编辑:慕编组成员(小天)