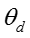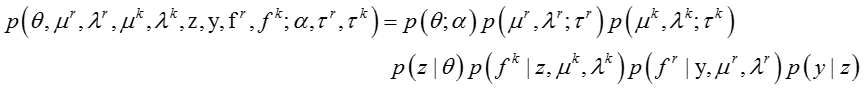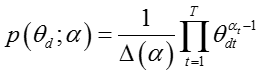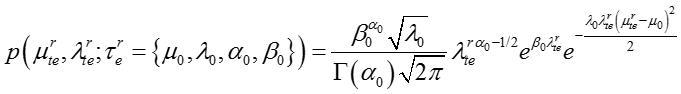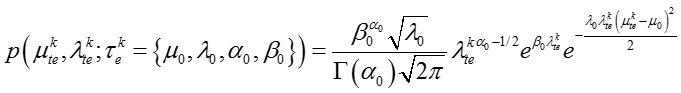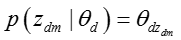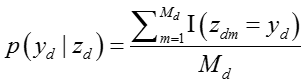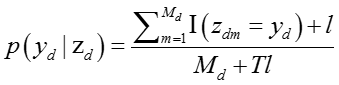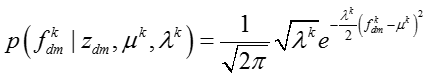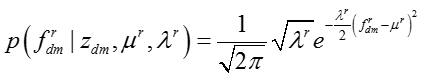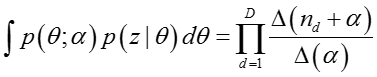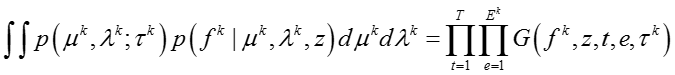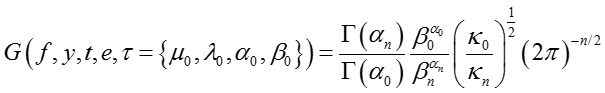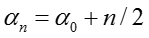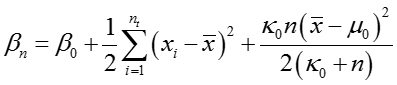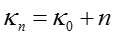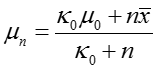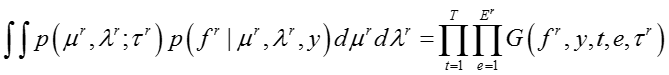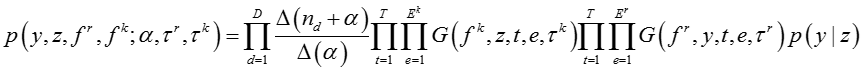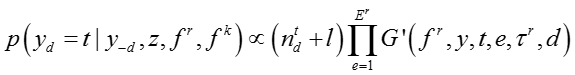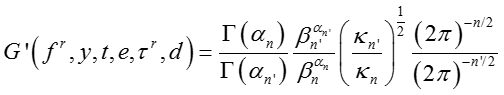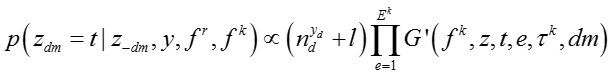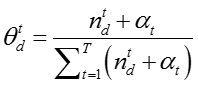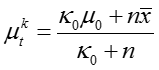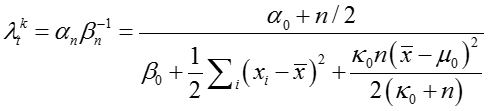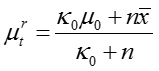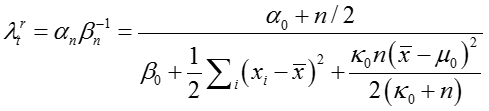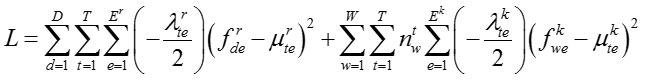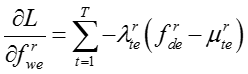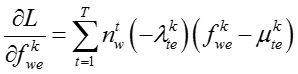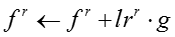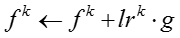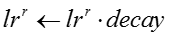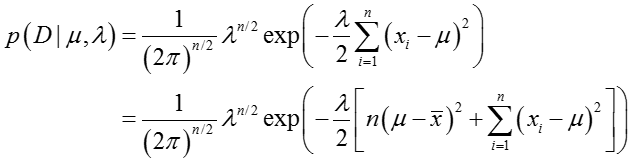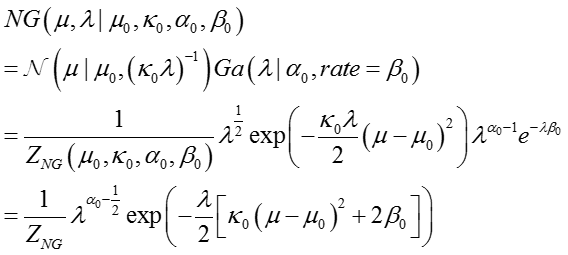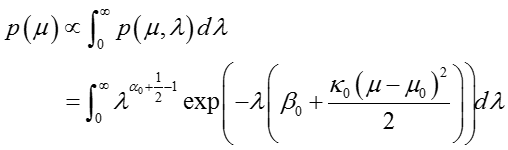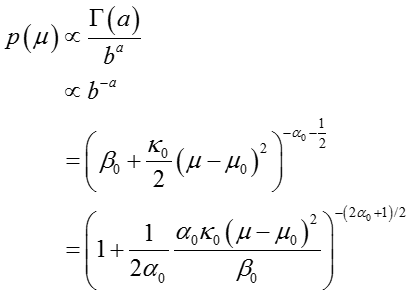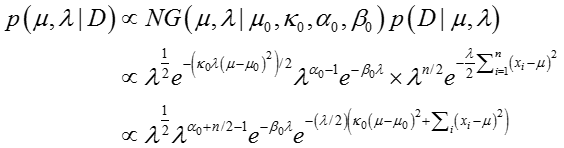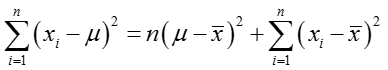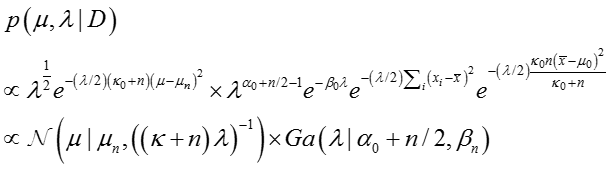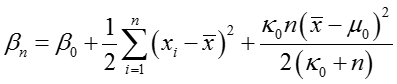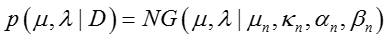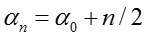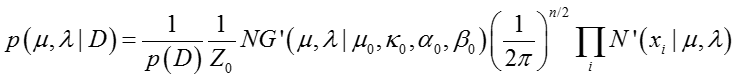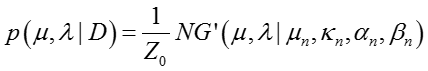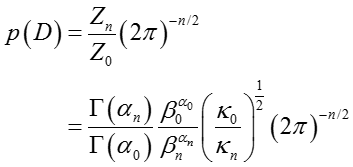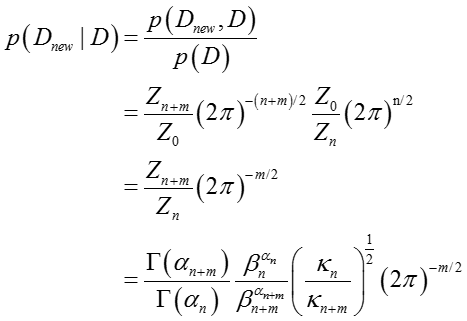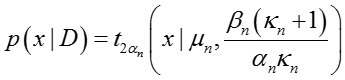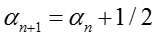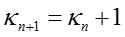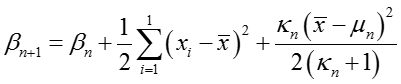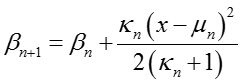2、Multi-Modal Bayesian Embeddings
2、Multi-Modal Bayesian Embeddings
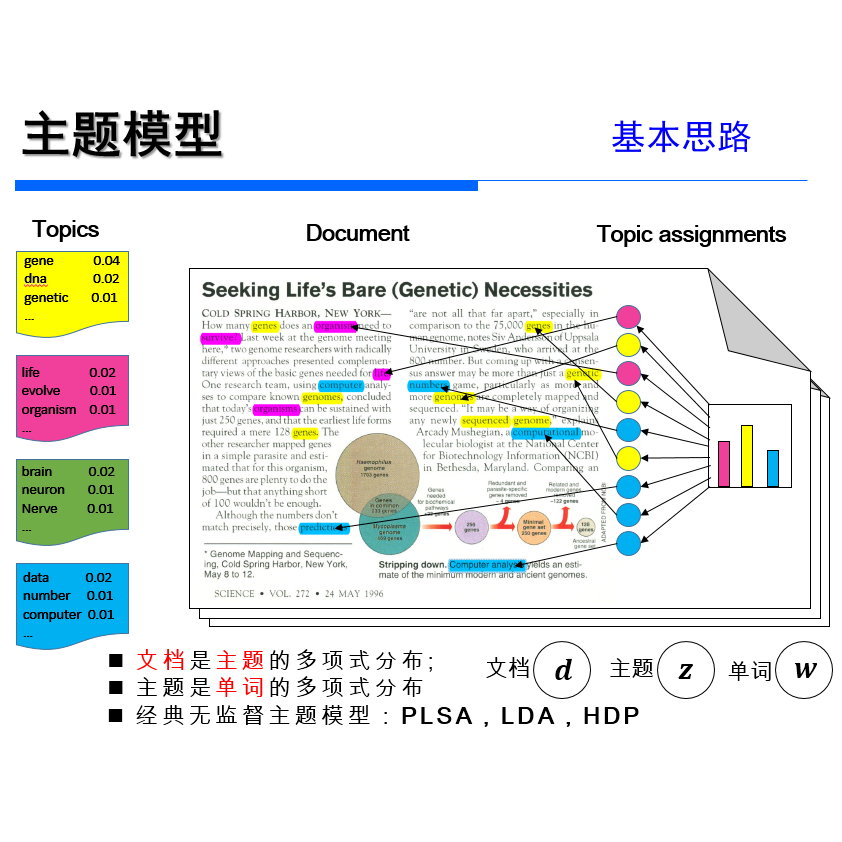
清华大学杨植麟提出一种异构贝叶斯嵌入模型,通过LDA主题模型简历异构的多模态嵌入表示之间的联系。
模型的输入是一系列弱监督信息,表示社交网络节点与文本的交互信息。仿照传统的话题模型,作者将一个弱监督信息条目称为一个文档。每一个文档包含了一个社交网络节点以及和该社交网络节点交互过的所有知识概念。下面,针对给定的弱监督信息进行建模。
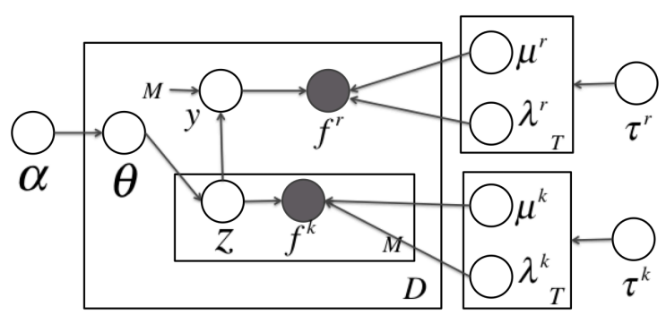
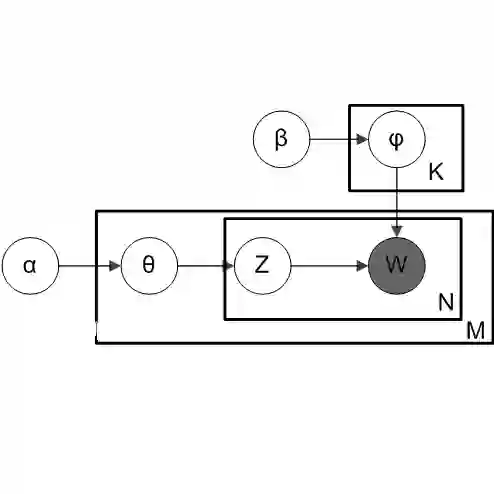
图:异构贝叶斯嵌入模型
上图是异构贝叶斯嵌入模型的图表示。在这个模型中,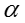
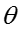
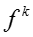
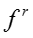
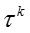
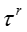
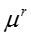
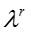
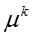
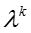
T 表示话题的数目, D 表示文档或社交网络节点的数目,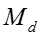
(1)模型生成过程
- 对于每一个话题 t
(a) 对于知识概念嵌入表示的每一个维度,从分布
生成
和
(b) 对于网络节点嵌入表示的每一个维度,从分布
生成
和
- 对于每一个文档 d
(a) 从
分布生成话题多项分布
(b) 对于文档中的每一个知识概念 w
i. 从多项分布
生成知识概念的话题 z
ii. 对于知识概念嵌入表示的每一个维度,从高斯分布
生成嵌入表示
© 从文档中所有知识概念的话题 z 中 uniform 生成网络节点的话题 y
(d) 对于网络节点嵌入表示的每一个维度,从高斯分布
生成嵌入表示
(2)联合概率分布推导
模型的联合概率分布可以写成如下形式:
下面我们对等式右边的每一项进行单独展开。
设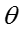
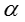
其中下标 d 表示文档,下标 t 表示话题。
高斯分布的参数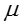
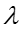
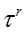
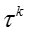
其中下标 t 表示话题, e 表示嵌入表示的某个维度, normal Gamma的超参数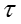
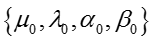
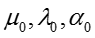
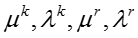
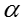
从多项分布生成话题的概率如下:
其中,下标 d 表示文档,下标 m 表示知识概念。
从知识概念的话题生成网络节点的话题的概率是一个 uniform分布,由于一个知识概念话题可能出现多次,所以该话题被生成的概率正比于出现次数:
其中,下标 d 表示文档,下标 m 表示知识概念。
如果我们采用上述式子作为生成网络节点话题的概率,网络节点的话题就必须在知识概念的话题中出现过,因为没有出现过的话题的概率是零。我们为了使得概率分布更加平滑,采用了拉普拉斯平滑的技巧,所以我们将生成网络节点话题的概率改写成:
其中拉普拉斯平滑系数
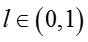
对于知识概念嵌入表示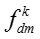
其中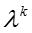
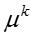
对于网络节点嵌入表示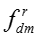
其中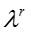
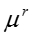
(3)对模型参数进行积分
在这一节中,作者借鉴 Collapsed Gibbs Sampling的思想,先对模型参数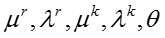
对参数 θ 进行积分。
其中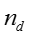
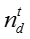
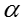
对参数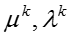
其中函数 G(·) 定义为,
其中 n 是所有 y = t 对应的 f 的数目。假设 x 是所有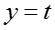
其中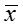
相似地,我们可以对参数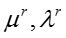
综合上面各个式子,我们可以得到对所有模型参数积分之后所有变量关于模型超参数的联合概率分布,
其中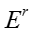
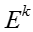
(4)条件概率推导
在本文中我们采用吉布斯采样对模型进行概率推理。为了进行吉布斯采样,我们需要推导每个变量在给定其他变量情况下的条件概率。对于文档
d,网络节点的话题 yd 的条件概率可以写成,
其中,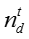
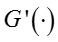
其中 n 是所有 y = t 对应的 f 的数目。假设 x 是所有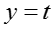
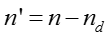
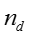
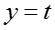
知识概念的话题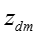
(5)模型参数更新
对于文档 d,话题分布参数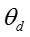
对于话题 t,假设 n
是所有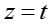
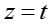
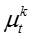

对于话题 t,假设 n 是所有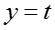
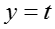
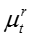
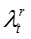
(6)嵌入表示更新
在之前的把嵌入表示模型和话题模型结合的高斯 LDA 模型中, Das
等人并没有对嵌入表示进行更新。我们在这个模型中,提出对嵌入表示也进行更新,可以更好地利用弱监督学习纠正非监督学习得到的嵌入表示的不足。
我们将目标函数定义为给定隐变量情况下的嵌入表示的对数似然,
其中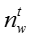
为了最大化嵌入表示的对数似然,我们可以直接从目标函数得到 closedform
的嵌入表示。但是因为我们每一次抽样的话题是具有随机性的,所以这样得到的嵌入表示容易受到话题的随机性的影响,变动太大。所以我们提出采用梯度下降的方法对嵌入表示进行更新。
知识概念和网络节点的嵌入表示的梯度分别为:
(7)模型学习过程
| 算法1:模型的学习过程 |
|---|
输入:训练数据D,模型超参数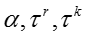 ,初始向量表示 ,初始向量表示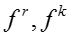 ,burn-in迭代次数 ,burn-in迭代次数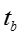 ,最大迭代次数 ,最大迭代次数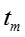 ,话题隐变量迭代次数 ,话题隐变量迭代次数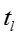 ,模型参数更新周期 ,模型参数更新周期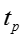 。 输出:话题隐变量 。 输出:话题隐变量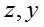 ,模型参数 ,模型参数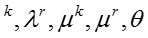 ,更新的向量表示 ,更新的向量表示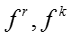 。 //初始化 随机初始化话题隐变量 。 //初始化 随机初始化话题隐变量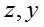 //Burn-in for //Burn-in for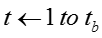 do foreach 网络节点话题隐变量 do foreach 网络节点话题隐变量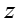 do 根据公式对 do 根据公式对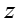 进行抽样生成 foreach 只是概念话题隐变量 进行抽样生成 foreach 只是概念话题隐变量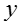 do 根据公式对 do 根据公式对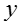 进行抽样生成 //抽样 for 进行抽样生成 //抽样 for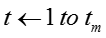 do for do for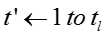 do foreach 网络节点话题隐变量 do foreach 网络节点话题隐变量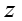 do 根据公式对 do 根据公式对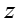 进行抽样生成 foreach 知识概念话题隐变量 进行抽样生成 foreach 知识概念话题隐变量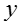 do 根据公式对 do 根据公式对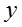 进行抽样生成 if 从上次参数读入已经经历了 进行抽样生成 if 从上次参数读入已经经历了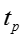 次迭代 then 根据公式读取参数 将当前读取参数与之前读取参数进行平均 对嵌入表示进行更新(根据下面的算法2) return 次迭代 then 根据公式读取参数 将当前读取参数与之前读取参数进行平均 对嵌入表示进行更新(根据下面的算法2) return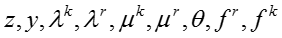 |
| 算法2:嵌入表示的更新过程 |
输入:模型参数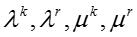 ,原来的嵌入表示 ,原来的嵌入表示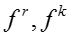 ,嵌入表示迭代次数 ,嵌入表示迭代次数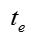 ,网络节点初始学习率 ,网络节点初始学习率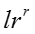 ,知识概念初始学习率 ,知识概念初始学习率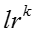 ,学习率衰减指数 ,学习率衰减指数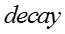 输出:新的嵌入表示 输出:新的嵌入表示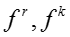 for for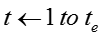 do do 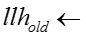 当前模型的对数似然 foreach 网络节点嵌入表示 当前模型的对数似然 foreach 网络节点嵌入表示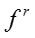 do 根据公式计算梯度 do 根据公式计算梯度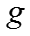 |
foreach 知识概念嵌入表示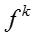
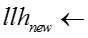
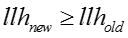
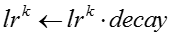
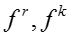
在“算法1”中,我们详细介绍了模型学习过程。模型的学习过程分为三个阶段:初始化,
burn-in,还有抽样阶段。
-
在初始化阶段,我们对话题隐变量 y 和 z 进行初始化,每个话题隐变量被uniform随机分配到一个话题。接着,我们采用 collapsed 吉布斯采样[24]的方法进行推理。在每一轮迭代中,我们固定其他变量的值,计算当前考察的变量在给定其他变量情况下的条件概率分布,然后从分布中进行抽样。
-
在 burn-in 阶段,我们根据公式 (3-2, 3-1)对话题隐变量进行抽样更新。在这一阶段,为了消除话题隐变量初始值对模型的影响,我们不更新模型参数或嵌入表示。
-
在模型的话题隐变量基本进入稳定状态之后,我们进入了抽样阶段。在抽样阶段,我们轮流对话题隐变量,模型参数和嵌入表示更新。话题隐变量的更新方法与burn-in 阶段相同。我们设置一个周期
,每一个周期我们计算一次模型参数,并进行累加。我们最后采用抽样阶段所有读取的模型参数的平均值作为最终的模型参数。
在“算法2”中,我们详细描述了对嵌入表示进行更新的算法流程。我们依次枚举每一个网络节点和知识概念,对于其嵌入表示,我们采用前面章节所推导得出的梯度进行梯度下降。
由于梯度下降的学习率比较难设置,我们使用了一个动态调整梯度下降学习率的技巧。每次进行梯度下降之前,先计算当前模型的对数似然,然后尝试进行梯度下降,再次计算迭代之后模型的对数似然。如果对数似然上升,说明当前的学习率合适,我们采用梯度下降之后的嵌入表示。如果对数似然下降,说明当前的学习率过大,我们把学习率乘以一个衰减指数,并放弃当前迭代对嵌入表示的更新。
附录1:后验预测推导
根据贝叶斯思想:
先验分布 * 似然函数 = 后验分布
先验分布:标准Gamma分布(normal-Gamma)
似然函数:高斯分布
后验分布:标准Gamma分布(normal-Gamma)
似然函数
先验分布
共轭先验分布满足标准Gamma分布(normal-Gamma),设先验参数为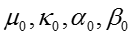
其中,先验分布中均值的边际分布如下:
从上述函数形式可以看出,这是一个非标准化的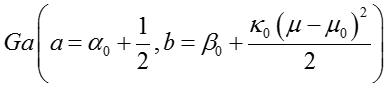
上述的分布可以认为是一个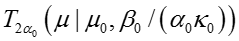
后验分布
后验分布可以由下面的式子获得:
其中
整理可得:
其中,
最终得到:
上式给出了后验分布与先验分布属于同类型的分布,即Gaussian分布和Gamma分布的乘积。同时推导出了模型参数更新公式。
边际似然函数
为了获得边际似然函数,我们利用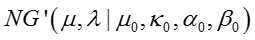
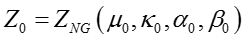
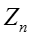
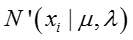
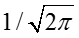
其中两
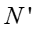
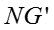
因此
后验预测(Posterior predictive)
对于m个新的观测数据,其分布预测概率如下:
在特殊情况下当m=1时,上式可以看出是一个T分布(T-distribution)
其中,后验参数更新如下:
当m=1时,有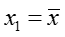
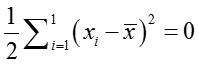
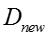

代换并化简可得:
可以看出,这是一个T分布,其中均值为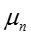
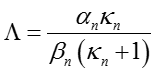
- Multi-Modal Bayesian Embeddings—Yang Z, Tang J, Cohen W. Multi-Modal Bayesian Embeddings for Learning Social Knowledge Graphs[J]. Computer Science, 201