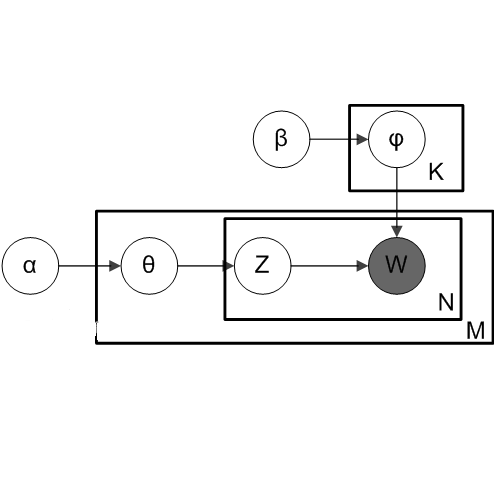
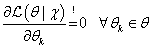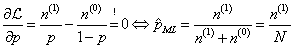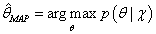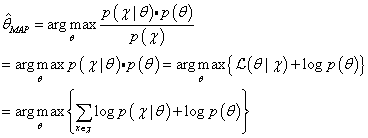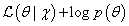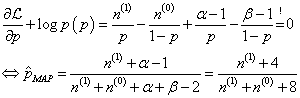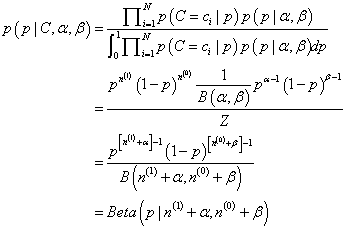1、机器学习——贝叶斯参数估计方法

  在介绍LDA模型之前，先介绍一下常见的参数估计方法，这对推断模型参数是非常必要的，往往是大家忽略的一个点。在参数估计中，我们会遇到两个主要问题：（1）如何去估计参数的值。 （2）估计出参数的值之后，如何去计算新的观测数据的概率，比如进行回归分析和预测。符号定义如下：
  现有观测数据 $\chi = \left\{ {{x_i}} \right\}_{i = 1}^{\left| \chi \right|}$，可以看作是一系列独立同分布的数据序列；其参数为 $\theta$，其取决于所依赖的分布，如高斯分布（Gaussian） $\theta = \left\{ {\mu ,{\sigma ^2}} \right\}$。
  对于这些数据和参数，在贝叶斯统计学中，存在一些很普遍的概率函数。这些概率函数将在贝叶斯规则中加以介绍，贝叶斯规则如下(公式(1))：

$p\left( {\theta |\chi } \right) = \frac{{p\left( {\chi |\theta } \right)p\left( \theta \right)}}{{p\left( \chi \right)}}$

针对上式，定义相关术语如下(公式(2))：

$posterior = \frac{{likelihoodprior}}{{evidence}}$

  下一段我们将介绍不同的参数估计方法，首先是最大似然估计，然后是最大后验估计（如何利用最大化后验合并参数中的先验知识），最后是贝叶斯估计（使用贝叶斯规则推断一个完整的后验分布）。

（1）最大似然估计（Maximum likelihood estimation, MLE）

  最大似然估计（Maximum likelihood）试图通过最大化似然函数估计出其参数。其含义是求出一个参数，使得已经发生的所有事件X的概率最大。最大似然估计就是要用似然函数取到最大值时的参数值作为估计值，似然函数可以写做公式(3)：

$L\left( {\theta |\chi } \right) \approx p\left( {\chi |\theta } \right) = \bigcap\limits_{x \in \chi } {\left\{ {X = x|\theta } \right\}} = \prod\limits_{x \in \chi } {p\left( {x|\theta } \right)}$

如公式(3)， $X$产生数据 $\chi$的联合事件的概率。根据公式3的结果，利用log似然进行最大似然估计更加简单。最大似然估计问题可以写成如下形式(公式(4))：

(由于公式编辑有问题，直接用图片代替了)
一般解决最大似然估计问题，通过求导似然函数，使其导数为零。根据上式，求解这个优化问题要对 $\theta$求导，得到导数为0的极值点。该函数取得最大值是对应的 $\theta$取值就是我们估计的模型参数。如下(公式(5))：

给定数据集 $\chi$，那么新的观测值 $\tilde x$发生的概率可以用公式6表示：

$\begin{array}{l} p\left( {\tilde x|\chi } \right) = \int_{\theta \in \Theta } {p\left( {\tilde x|\theta } \right)} p\left( {\theta |\chi } \right)d\theta \\ \approx \int_{\theta \in \Theta } {p\left( {\tilde x|{{\hat \theta }_{ML}}} \right)} p\left( {\theta |\chi } \right)d\theta = p\left( {\tilde x|{{\hat \theta }_{ML}}} \right) \end{array}$

注意有一个约等于，因为他进行了一个近似的替换，将 ${\hat \theta _{ML}}$替换成了待估计的真实参数值 $\theta$，便于计算。也就是说，新的样本的分布服从估计的参数 ${\hat \theta _{ML}}$。

举例

  举个例子，以抛硬币伯努利实验为例。考虑N次伯努利实验的集合，每次抛硬币的概率为参数p，不妨设为硬币是正面的概率。例如，伯努利实验通过投掷一枚有变形的硬币来实现。对于一次实验来说，伯努利概率密度函数如下(公式(8))：

$p\left( {C = c|p} \right) = {p^c}{\left( {1 - p} \right)^{1 - c}}\approx Bern\left( {c|p} \right)$

我们定义c=1为硬币的正面朝上；定义c=0为硬币反面朝上。
  基于参数p构建最大似然估计，log似然函数如下所示(公式(9))：

其中， ${n^{\left( c \right)}}$是伯努利实验中事件c发生的次数；对参数p求偏导数，得到参数p的最大似然估计值为：

也就是正面事件次数与样本总数的比值，如果硬币是有形变的，那么经过20次抛掷以后，可能得到结果 ${n^{\left( 1 \right)}}$=12，即12次正面和 ${n^{\left( 0 \right)}}$=8，即8次反面。在最大似然估计中得到结果 =12/20=0.6。

（2）最大后验估计（Maximum a posteriori , MAP）

最大后验估计（Maximum a posteriori, MAP）与最大似然估计方法类似，区别是最大后验概率估计在参数中考虑了先验知识，用先验分布 $p\left( \theta \right)$加权参数。这种方法不是要求似然函数最大，而是要求由贝叶斯公式计算出的整个后验概率最大(公式(12))：

利用贝叶斯规则，上式可写为(公式(13))：

对比公式(4)，在似然函数中增加了先验分布。先验分布 $p\left( \theta \right)$可以编码额外的数据以防止过度拟合，通过优先执行更简单的模型，这种方法被称为奥卡姆剃刀（Occam’s razor）。
MAP参数估计可以通过最大化

来实现，与公式6类似，给定观测到的样本数据 $\chi$，一个新的样本值 $\tilde x$发生的概率是：

$p\left( {\tilde x|\chi } \right) \approx \int_{\theta \in \Theta } {p\left( {\tilde x|{{\hat \theta }_{MAP}}} \right)} p\left( {\theta |\chi } \right)d\theta = p\left( {\tilde x|{{\hat \theta }_{MAP}}} \right)$

与最大似然估计相比，现在需要多加上一个先验分布概率的对数。在实际应用中，这个先验可以用来描述人们已经知道或者接受的普遍规律。例如在扔硬币的试验中，每次抛出正面发生的概率应该服从一个概率分布，这个概率在0.5处取得最大值，这个分布就是先验分布。先验分布的参数我们称为超参数(hyperparameter)。 所以我们认为， $\theta$也是服从一个先验分布的：alpha是他的超参数,即 $p\left( \theta \right): = p\left( {\theta |\alpha } \right)$。

举例

下面以Beta分布举例：

$p\left( {p|\alpha ,\beta } \right) = \frac{1}{{B\left( {\alpha ,\beta } \right)}}{p^{\alpha - 1}}{\left( {1 - p} \right)^{\beta - 1}} = Beta\left( {p|\alpha ,\beta } \right)$

其中，Beta函数 $B\left( {\alpha ,\beta } \right) = \frac{{\Gamma \left( \alpha \right)\Gamma \left( \beta \right)}}{{\Gamma \left( {\alpha + \beta } \right)}}$，符号 $\Gamma \left( x \right)$表示Gamma函数，Gamma函数有一条性质 $x! = \Gamma \left( {x + 1} \right)$。Beta分布的区间为[0,1]，因此可以用来生成归一化的概率值。Beta分布的概率密度函数如下图1所示。由图可知，不同参数的Beta分布其形状差异很大，可以模拟不同的数据分布。

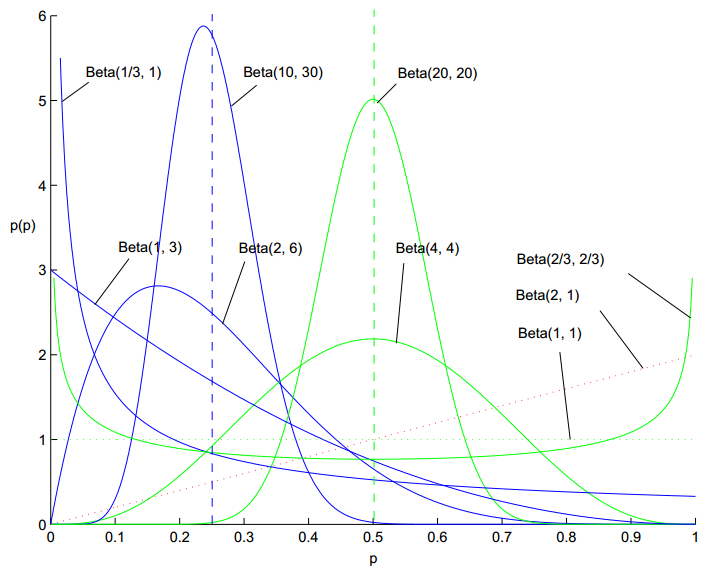
举个例子，我们可以在抛硬币的实验中把先验Beta分布的参数设置为 $\alpha = \beta = 5$，这样，这样先验分布在0.5处取得最大值（观察上面的图可知，当超参数 $\alpha$和 $\beta$是相等的，先验分布在p等于0.5时，取得极大值）。现在我们来求解MAP估计函数的极值点，同样对p求导数，得到参数p的的最大后验估计值为：

与最大似然估计ML的结果对比可以发现结果中多了 $\alpha-1$, $\alpha + \beta - 2$，我们称这两者为pseudo count伪计数，这两项的作用是使总概率p向0.5拉近，因为我们的先验（其参数 $\alpha$和 $\beta$为5）认为就是约等于0.5的。上面的伪计数就是先验在起作用，并且超参数越大，为了改变先验分布传递的信息其所需要的观测数目就越多，此时对应的Beta函数越聚集，紧缩在其最大值两侧。
  如果我们做20次实验，出现正面12次，反面8次，那么，根据MAP估计出来的参数p为（12+4）/(20+8) = 16/28 = 0.571,小于最大似然估计得到的值0.6，这也显示了先验对“硬币一般是两面均匀的”的参数估计的影响。

（3）贝叶斯估计

贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。极大似然估计和极大后验概率估计，都求出了参数的值，而贝叶斯推断则不是，贝叶斯推断扩展了极大后验概率估计MAP方法，它根据参数的先验分布 $p\left( \theta \right)$和一系列观测数据 $\chi$，求出参数 $\theta$的后验分布 $p\left( {\theta |\chi } \right)$，然后可以用后验分布 $p\left( {\theta |\chi } \right)$的期望作为参数的最终值，也可以得到后验分布 $p\left( {\theta |\chi } \right)$的一个方差量，来评估参数估计的准确程度或者置信度。

又回到贝叶斯公式(18)：

$p\left( {\theta |\chi } \right) = {{p\left( {\chi |\theta } \right)p\left( \theta \right)} \over {p\left( \chi \right)}}$

其中是 $p\left( \theta \right)$先验概率， $p\left( {\theta |\chi } \right)$是后验概率， $p\left( {\chi |\theta } \right)$是似然， $p\left( \chi \right)$是证据（Evidence）即观测到数据的概率，要求 $p\left( \chi \right)$其全概率展开公式(19)：

$p\left( \chi \right) = \int_{\theta \in \Theta } {p\left( {\chi |\theta } \right)p\left( \theta \right)d} \theta$

当新的数据被观察到时，后验概率可以自动随之调整。但是上式中的全概率公式的求解方法通常是贝叶斯推断中最复杂的部分（MAP直接忽略了分母），下面将进行详细介绍。

用贝叶斯估计来做预测问题时，如果我们想估计一个新样本的概率，可以由下面公式来计算：

$p\left( {\tilde x|\chi } \right) = \int_{\theta \in \Theta } {p\left( {\tilde x|\theta } \right)p\left( {\theta |\chi } \right)d} \theta$

$= \int_{\theta \in \Theta } {p\left( {\tilde x|\theta } \right){{p\left( {\chi |\theta } \right)p\left( \theta \right)} \over {p\left( \chi \right)}}d} \theta$

上式中，后验概率 $p\left( {\theta |\chi } \right)$取代了直接计算参数 $\theta$（可以和MLE，MAP对比一下），公式中将先验知识融入到概率预测中。

举个例子，N次伯努利实验，参数p（即正面的概率）的先验分布是参数为（5,5）的beta分布，然后接下来，我们根据参数p的先验分布和N次伯努利实验结果来求p的后验分布。我们假设先验分布为Beta分布，但是构造贝叶斯估计时，不是要求用后验最大时的参数来近似作为参数值，而是求满足Beta分布的参数p的后验分布的期望，也就是直接写出参数的分布再来求分布的期望：

其中，C是抛掷硬币的所有实验结果，C=0或1。由上式可知，其后验分布还是服从Beta分布的概率密度函数。根据分布的均值（mean） $\left\langle {p|\alpha ,\beta } \right\rangle = \alpha {\left( {\alpha + \beta } \right)^{ - 1}}$和方差（variance） $V\{p|\alpha,\beta\}= \alpha \beta {\left( {\alpha + \beta + 1} \right)^{ - 1}}{\left( {\alpha + \beta } \right)^{ - 2}}$，估计结果如下：

$\left\langle {p|C} \right\rangle = {{{n^{\left( 1 \right)}} + \alpha } \over {{n^{\left( 1 \right)}} + {n^{\left( 0 \right)}} + \alpha + \beta }} = {{{n^{\left( 1 \right)}} + 5} \over {N + 10}}$

$V\{p|C\}= {{\left( {{n^{\left( 1 \right)}} + \alpha } \right)\left( {{n^{\left( 0 \right)}} + \beta } \right)} \over {\left( {N + \alpha + \beta + 1} \right){{\left( {N + \alpha + \beta } \right)}^2}}} = {{\left( {{n^{\left( 1 \right)}} + 5} \right)\left( {{n^{\left( 0 \right)}} + 5} \right)} \over {\left( {N + 11} \right){{\left( {N + 10} \right)}^2}}}$

可以看出此时估计的参数p对应的后验分布的期望和最大似然估计（MLE），最大后验估计（MAP）中得到的估计值都不同，此时如果仍然是做20次实验，12次正面，8次反面，那么我们根据贝叶斯估计得到的参数p满足参数为12+5和8+5的Beta分布，其均值和方差分别是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此时求出的p的期望比MLE和MAP得到的估计值都小，更加接近0.5。

上面就是关于机器学习最基本的参数估计概念的一个总结，建议大家多多体会极大似然估计，最大后验估计，贝叶斯估计这三者的相同点和不同点，有什么问题可以在我们的专知公众号平台上交流或者加我们的专知-人工智能交流群 426491390

同时请，关注我们的公众号，获取最新关于专知以及人工智能的资讯、技术、算法等内容。扫一扫下方关注我们的微信公众号。

参考文献

1. http://www.arbylon.net/publications/text-est.pdf —《Parameter estimation for text analysis》