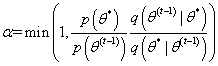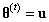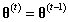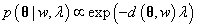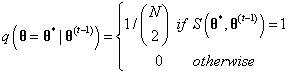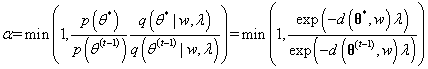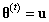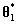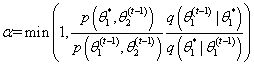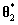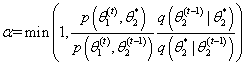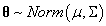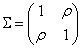2、马尔科夫链蒙特卡洛采样( Markov Chain Monte Carlo,MCMC )
马尔科夫链蒙特卡洛采样( Markov Chain Monte Carlo,MCMC )
一直想把马尔科夫链蒙特卡洛采样的详细过程总结并写出来,尽管网上的中文教材比较多,但暂时没有发现写的比较浅显易懂并且条理分明的博客文章,偶然间看到这个英文教程,清晰地记得那时候花一天时间通读全文,并且代码跑通实现了,很多以前是懂非懂的采样问题突然清晰明白了,现在花时间整理,并且把英文教程前两章翻译出来,希望对大家有用,有问题或者理解有偏差的地方,欢迎指出来,一起学习进步。
1、从随机变量中采样
研究人员提出的概率模型对于分析方法来说往往过于复杂。越来越多的研究人员依赖数学计算的方法处理复杂的概率模型,研究者通过使用计算的方法,摆脱一些分析技术所需要的不切实际的假设。(如,常态和独立)
大多数近似方法的关键是在于从分布中采样的能力。我们需要通过采样来预测特定的模型在某些情况下的行为,并为潜在的变量(参数)找到合适的值以及将模型应用到实验数据中。大多数采样方法都是将复杂的分布中抽样的问题转化到简单子问题的采样分布中。
本章,我们解释两种采样方法:逆变换方法(the inverse transformation method)和拒绝采样(rejection sampling)。这些方法主要适用于单变量的情况,用于处理输出单变量的问题。在下一章,我们讨论马尔科夫链蒙特卡洛方法(Markov chain Monte Carlo),该方法可以有效的用于多元变量分布采样。
1.1 标准分布
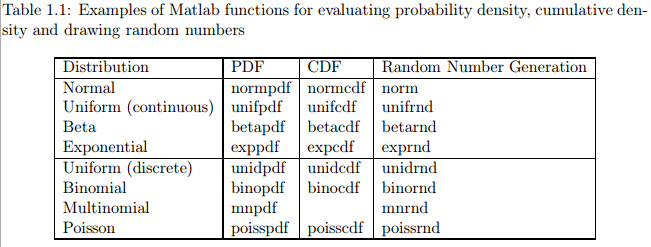
有一些分布被经常用到,这些分布被MATLAB作为标准分布实现。在MATLAB统计工具箱(Matlab Statistics Toolbox supports)实现了一系列概率分布。使用MATLAB工具箱可以很方便的计算这些分布的概率密度、累积密度、并从这些分布中取样随机值。表1.1列举了一些MATLAB工具箱中的标准分布。在MATLAB文档中列举了更多的分布,这些分布可以用MATLAB模拟。利用在线资源,通常很容易能找到对其他常见分布的支持。
为了说明如何使用这些函数,Listing 1.1展示了正态分布 可视化的MATLAB代码,其中 。
举例
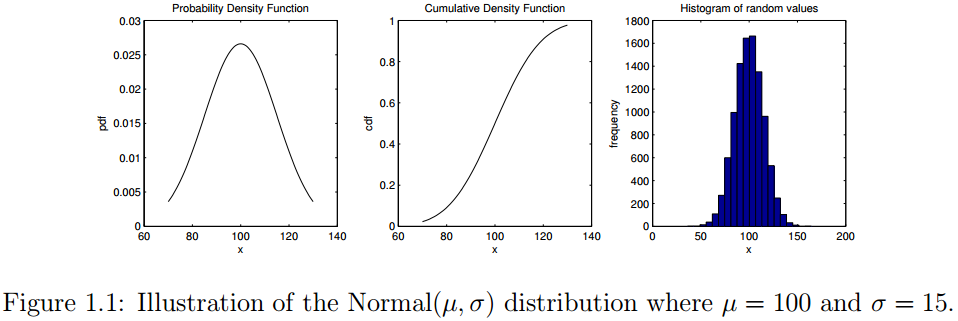
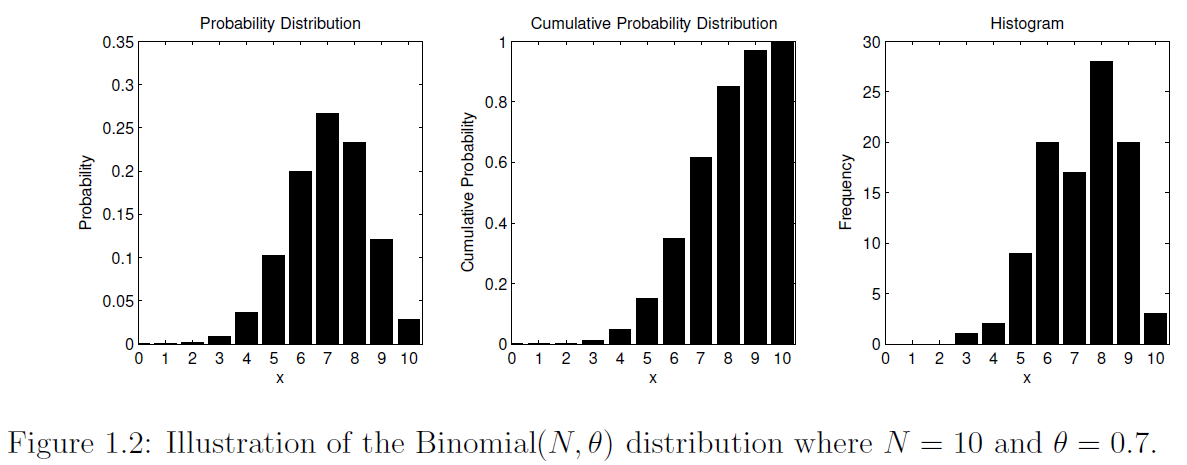
举个例子,可以想象一下用该正态分布表示观察到的人群的IQ系数变化。该代码显示了了如何展示概率密度和累积密度。它还展示了如何从该分布中抽取随机值以及如何使用hist函数可视化这些随机样本。代码的输出结果如图1.1所示。类似的,图1.2可视化离散的二项分布 ,其中参数 , 。该分布可认为是进行10次实验,每次试验成功的概率是 。(所有代码见最后百度云链接)
1 %% Explore the Normal distribution N( mu , sigma )
2 mu = 100; % the mean
3 sigma = 15; % the standard deviation
4 xmin = 70; % minimum x value for pdf and cdf plot
5 xmax = 130; % maximum x value for pdf and cdf plot
6 n = 100; % number of points on pdf and cdf plot
7 k = 10000; % number of random draws for histogram
8
9 % create a set of values ranging from xmin to xmax
10 x = linspace( xmin , xmax , n );
11 p = normpdf( x , mu , sigma ); % calculate the pdf
12 c = normcdf( x , mu , sigma ); % calculate the cdf
13
14 figure( 1 ); clf; % create a new figure and clear the contents
15
16 subplot( 1,3,1 );
17 plot( x , p , 'k−' );
18 xlabel( 'x' ); ylabel( 'pdf' );
19 title( 'Probability Density Function' );
20
21 subplot( 1,3,2 );
22 plot( x , c , 'k−' );
23 xlabel( 'x' ); ylabel( 'cdf' );
24 title( 'Cumulative Density Function' );
25
26 % draw k random numbers from a N( mu , sigma ) distribution
27 y = normrnd( mu , sigma , k , 1 );
28
29 subplot( 1,3,3 );
30 hist( y , 20 );
31 xlabel( 'x' ); ylabel( 'frequency' );
32 title( 'Histogram of random values' );
Listing 1.1: Matlab code to visualize Normal distribution.
1.2 从非标准分布中采样
我们希望MATLAB工具也支持从非标准分布中采样,这种情况在建模过程中经常出现,因为研究人员可以提出一种新的噪声过程或已存在分布的组合方式。复杂采样问题的计算方法通常依赖于我们已经知道如何有效地进行采样的分布。这些从简单分布中采样的随机值可以被转换成目标分布需要的值。事实上,这一节我们讨论的一些技术是MATLAB的内部分布,如正态分布和指数分布。
1.2.1 用离散变量进行逆变换采样(Inverse transform sampling)
逆变换采样(也被成为逆变换方法)即给定累积分布函数的逆,可从任意概率分布中生成随机数。这个方法是对均匀分布的随机数字进行采样(在0到1之间)然后使用逆累积分布函数转换这些值。该过程的简单之处就在于,潜在的采样仅仅依赖对统一的参数进行偏移和变换。该过程可以用于采样很多不同种类的分布,事实上,MATLAB实现很多随机变量生成方法也是基于该方法的。
在离散分布中,我们知道每个输出结果的概率。这种情况下,逆变换方法就需要一个简单的查找表。
给定一个非标准的离散分布的例子,我们使用一些实验数据来研究人类如何能产生一致的随机数(如Treisman and Faulkner,1987)。在这些实验中,被测试者会产生大量的随机数字(0,…,9)。研究人员根据每个随机数字的相对频率进行制表。你可能会怀疑实验对象不会总是产生均匀分布。表1.2.1展示了一些典型的数据,其中可以看出一些比较低的和高的数字容易被忽视,而一些特殊数字(如数字4)占过高的比例。由于某种原因,数字0和9从来没有被产生。在任何情况下,这些数字都是相当典型的,而且证明了人类不能很好地产生均匀分布的随机数字。
假设我们想要模拟这个过程,并根据表1.2.1中的概率编写一个算法采样数字。因此,程序应该用概率0.2生成数字4,根据概率0.175生成数字5等。例如,Listing1.2中的代码使用MATLAB内置的函数randsample来实现这个过程。代码的输出结果如图1.2.1所示。
1 % Simulate the distribution observed in the
2 % human random digit generation task
3
4 % probabilities for each digit
5 theta = [0.000; ... % digit 0
6 0.100; ... % digit 1
7 0.090; ... % digit 2
8 0.095; ... % digit 3
9 0.200; ... % digit 4
10 0.175; ... % digit 5
11 0.190; ... % digit 6
12 0.050; ... % digit 7
13 0.100; ... % digit 8
14 0.000 ] ... % digit 9
15
16 % fix the random number generator
17 seed = 1; rand( 'state' , seed );
18
19 % let's say we draw K random values
20 K = 10000;
21 digitset = 0:9;
22 Y = randsample(digitset,K,true,theta);
24 % create a new figure
25 figure( 1 ); clf;
26
27 % Show the histogram of the simulated draws
28 counts = hist( Y , digitset );
29 bar( digitset , counts , 'k' );
30 xlim( [ −0.5 9.5 ] );
31 xlabel( 'Digit' );
32 ylabel( 'Frequency' );
33 title( 'Distribution of simulated draws of human digit generator' );
Listing 1.2: Matlab code to simulate sampling of random digits.
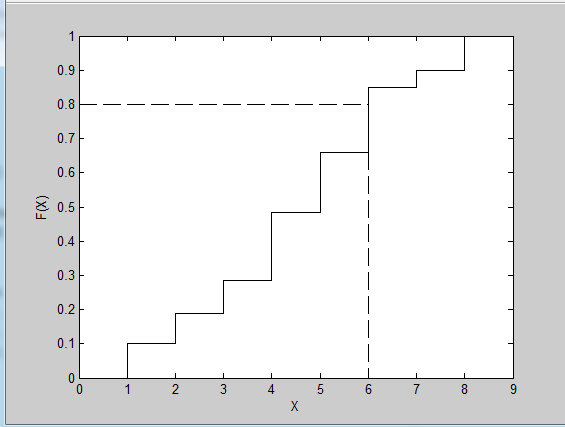
Figure 1.2.1: Illustration of the inverse transform procedure for generating discrete random variables. Note that we plot the cumulative probabilities for each outcome. If we sample a uniform random number of U = 0.8, then this yields a random value of X = 6
如果不采用内置的函数如randsample 和mnrnd,而是通过逆变换方法来实现底层的采样算法对我们更有帮助。我们首先需要计算累计概率分布,换句话说,我们需要知道我们观察到的结果等于或小于某一特定值的概率。如果 表示累计函数,我们需要计算 。对于离散分布,计算这个值可以通过简单的求和。我们的例子的累计概率在表1.2.1的最后一列中给出。在逆变换算法中,该想法是采样随机偏差(0和1之间的随机数)并将随机数与表中的累计概率比较。随机偏差的第一个结果小于(或等于)相关的累计概率与抽样结果相对应。图1.2.1展示了一个例子,其中随机偏差 ,导致采样结果 。这个重复采样随机偏差的过程,并与累积分布相比较,就会形成离散变量的逆变换方法的基础。注意我们应用了一个逆函数,因为做的是逆表的查找。
1.2.2 连续变量的逆变换采样
逆变换样方法也可以用于连续分布。一般地,该方法目的是获得均匀的随机偏差并且将逆函数应用在随机偏差的累积分布中。下面,令 是目标变量 的累积密度函数(cumulative density function,CDF), 是该函数的逆。我们希望获得随机变量 的值,可以通过如下步骤获取:
- 获得均匀分布
- 设
- 重复上述采样过程
可通过一个简单的例子解释上述方法。假设我们要从指数分布(exponential distribution)中采样随机数。当 时,累积密度函数是 。用一些简单的代数方法,就可以求出这个函数的逆 。从而引出了下面的从 分布中采样随机数的步骤:
- 获得均匀分布
- 设
- 重复上述采样过程
1.2.3 拒绝采样
在很多情况下,逆变换采样方法是不适用的,因为很难计算其累积分布和它的逆。在这种情况下,有其他的可供选择的采样方法,如拒绝采样,以及其他使用马尔科夫链蒙特卡洛的方法,将在下一章进行讨论。拒绝采样的主要优势在于它不需要“burn-in”过程。和其他方法相反,所有的样本在采样过程中获得,并且可直接作为目标分布的样本。
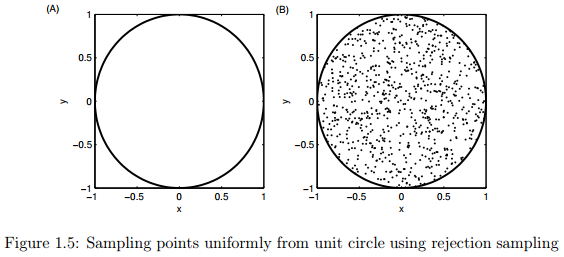
拒绝采样的一般概念可用图1.5进行解释。假设我们想在以 为圆心以1为半径的圆形内均匀画点。乍一看,似乎很难均匀地在这个圆内直接进行采样。但是我们可以应用拒绝采样的方法进行采样,首先确定圆外围的正方形,在正方形中采样 的值,剔除满足式子 的所有的取值。注意在这个过程中我们使用了一个简单的建议分布( ),如均匀分布,作为从更复杂的分布中采样的基础。
拒绝采样允许我们从难以采样的分布中生成样本,在这些难以采样的分布中我们可以计算任何特定样本的概率。换句话说,假定我们有一个分布 ,并且难以直接从该分布中采样,但是我们可以计算其特定值的概率密度 。
第一件要做的就是建议分布(proposal distribution)。建议分布就是指一个简单的分布,记为 ,该分布是可以直接进行采样的。主要思路是,计算同时满足建议分布和目标分布采样的概率,然后拒绝相对于建议分布中那些不太可能出现在目标分布下的样本。
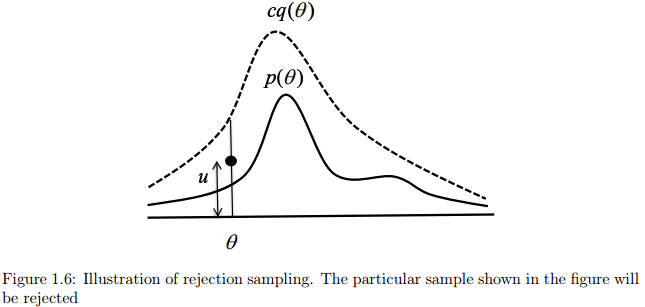
图1.6说明了这个过程。我们首先需要找到一个常量 使之对所有的可能的样本 满足 。建议函数 乘以常量 被称为比较分布,并且使其总是大于目标分布。要确定常数 并不容易,我们先假定可以通过微积分确定该常数。我们首先从均匀分布 中获取一个数 ,换句话说,这是直线段从0到 的某个点以 为建议的比较分布。如果 ,我们拒绝这个建议分布采样得到的值,否则,接受之。如果接受了某个建议,则采样值 就是从目标分布 中获得的。上述的采样过程步骤如下:
| 步骤 |
|---|
-
选择一个容易采样的分布
-
确定常量 ,使对所有 的有
-
从建议分布 中采样一个建议样本
-
从区间 采样一个数
-
如果 则拒绝,否则接受
-
重复步骤3,4,5,直到达到要求的样本数量;每个接受的样本都是从 中获得的
这种算法有效的关键就是需要有尽可能多的样本被接受,这取决于建议分布 的选择。建议分布不同于目标分布,它会导致很多拒绝接受的样本,这将减慢采样的速度。
2、马尔科夫链蒙特卡洛理论(MCMC)
将概率模型应用到数据中,常需要复杂的推理过程,需要用到复杂的、高维的分布。马尔科夫链蒙特卡洛理论(MCMC)是一种通用的计算方法,通过迭代地对生成的样本进行求和代替复杂的数学推理。比较棘手的问题分析方法通常可以用某种形式的MCMC来解决,即便是高维的问题也同样如此。MCMC的发展可以说是统计学计算方法的最大进步。MCMC是一个非常活跃的研究领域,现在也有一些标准化的技术被广泛应用。本章,我们讨论两种形式的MCMC方法:Metropolis-Hastings和Gibbs Sampling。在我们学习这些技术之前,我们首先要了解下面两种主要思想:蒙特卡洛积分和马尔科夫链(Monte Carlo integration, and Markov chains)。
2.1 蒙特卡洛积分(Monte Carlo integration)
概率推理中的很多问题需要复杂的积分计算或者对非常大的空间中的数据求和。例如,一个常见的问题是计算对于随机变量 的函数 的期望值(简单起见,我们设是 单随机变量)。如果 是连续的,函数期望定义如下:
如果 是离散变量,则积分被求和取代:
很多情况下,我们想要计算统计量的均值和方差。例如,对 ,我们要计算分布的均值,使用积分或求和的分析技术对于某些特定分布具有很大的挑战性。例如,密度 的函数可能不能进行积分。对于离散分布,可能由于结果空间太大而不能进行显式的求和。
蒙特卡洛积分方法一般的想法是使用样本近似估计复杂分布的期望。具体地,我们获得一系列样本 ,这些样本从 中独立获得。在这种情况下,我们可以使用有限样本的累加近似估计期望:
在上述过程中,我们用适当样本的求和来代替积分。一般来说,近似计算的精确度可以通过增加 来提高。另外需要注意的是,近似计算的精确度取决于样本之间的独立性。当样本相互关联的时候,有效样本的数量减少了,这是MCMC的存在的一个潜在的问题。
2.2 马尔科夫链
Markov链是一个随机过程,我们利用顺序过程从一个状态过渡到另一个状态。我们在状态 开始Markov链,使用转移函数 作为状态的转移矩阵,确定下一个状态 。然后以 作为开始状态使用同样的转移函数继续确定下一个状态,如此重复,得到一系列状态:
这样一个状态序列就被称为马尔科夫链(Markov chain)。生成一个包含 个状态的马尔科夫链的过程如下:
| 步骤 |
|---|
-
设
-
生成一个初始值 ,并设
-
重复下列过程
从转移函数 中采样一个新的值
设
- 直到
在上述迭代过程中,马尔科夫链的状态 仅仅是根据上一个状态 产生的。因此,马尔科夫链向新的状态转移总是只依赖最后一个状态。这是MCMC中使用马尔科夫链的很重要的一个属性。
当初始化每个马尔科夫链的时候,马尔科夫链将会在状态空间中进行状态转移。如果我们开始一系列的马尔科夫链,每一个链赋予不同的开始状态,通过一系列的状态转移过程,最终每个链都将处于接近起始状态的某个状态,这个过程被称为“burn-in”。马尔科夫链的一个重要的性质是,链的起始状态经过足够次数的转换后最终的状态不会受初始状态的影响(假定满足马尔科夫链的某些条件),也就是说,马尔科夫链经过有限次的状态转移之后,最终能达到稳定的状态,被称为平稳分布,从其平稳分布中可以反映样本。当满足一定的条件时,无论从哪个状态开始,马尔科夫链最终都会到达一个确定的稳定状态。应用到MCMC中,它允许我们从一个分布中连续地采样,且序列的初始状态不会影响估计过程。
举例
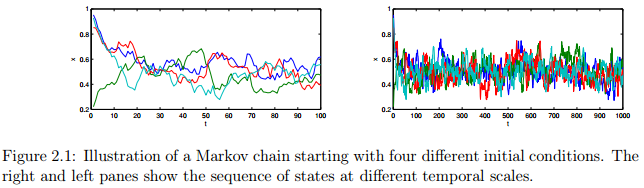
举个例子:图2.1展示了一个马尔科夫链的例子,为简单起见,以单个连续变量为例。从Beta分布中进行采样,分布函数为 。从四个不同的起始状态开始,每个链都有 次迭代。图中的两个子图分别展示了不同时刻的状态序列,线的颜色代表不同的链。注意,前10次迭代显示了序列对初始状态的依赖,这是“burn-in”过程。接下来序列的剩余部分是稳定状态(如果不停止,那么继续保持稳定状态)。那么我们如何确切知道稳定状态到达的时间,又怎么知道链是收敛的呢?要解释上述问题并不是容易的,尤其是在高维状态空间中。
2.3 综合讲解:马尔科夫链蒙特卡洛理论
前面两个部分讨论了MCMC理论背后的主要思想,蒙特卡洛采样和马尔科夫链。蒙特卡洛采样提供估计分布的各种特征:如均值,方差,峰值,或者其他的研究人员感兴趣的统计特征。马尔科夫链包含一个随机的顺序过程,并从平稳分布中采样状态。
MCMC的目标是设计一个马尔科夫链,该马尔科夫链的平稳分布就是我们要采样的分布,这就是所谓的目标分布。换句话说,我们希望从马尔科夫链的状态中采样等同于从目标分布中取样。这个想法是用一些方法设置转移函数,使无论马尔科夫链的初始状态是什么最终都能够收敛到目标分布。有很多方法使用相对简单的过程实现这个目标,我们在这里只讨论Metropolis,Metropolis Hastings和 Gibbs sampling。
2.4 Metropolis Sampling
Metropolis Sampling是最简单的MCMC方法,是Metropolis Hastings Sampling的一个特例,Metropolis Hastings
Sampling将在下一节讨论。假设我们的目标是从目标密度函数
中采样,其中
。Metropolis sampler创建一个马尔科夫链并且产生一系列值:
其中 表示马尔科夫链在第 次迭代的状态。当“burn-in”过程之后,即达到平稳分布之后,从马尔科夫链中采样的样本反映了从目标分布 中的采样样本。
在Metropolis过程中,给第一个状态 初始化一些值。我们然后使用建议分布 (建议分布一般是非常简单的分布)生成一个候选节点 ,该节点是在上一个状态的基础上生成的。下一步就是接受或者拒绝该建议。接受建议的概率是公式2.6:
为了决定是否接受该建议,我们定义一个偏差变量 ,如果 ,我们接受这个建议,并将下一个状态设置为该建议: 。如果,我们拒绝该建议,下一个状态就设置为前一个状态:。我们根据当前的状态继续提出新的建议状态,然后接受或拒绝该状态,直到采样器达到收敛。收敛时节点 处的样本反映了从目标分布 中采样的样本。下面是Metropolis采样器的步骤:
| 步骤 |
|---|
-
设
-
生成一个初始值,并设
-
重复下列过程:
从 中生成一个建议
计算接受该建议的概率
从均匀分布 中生成一个值
如果 ,接受该建议且设置 ;否则设置
- 直到
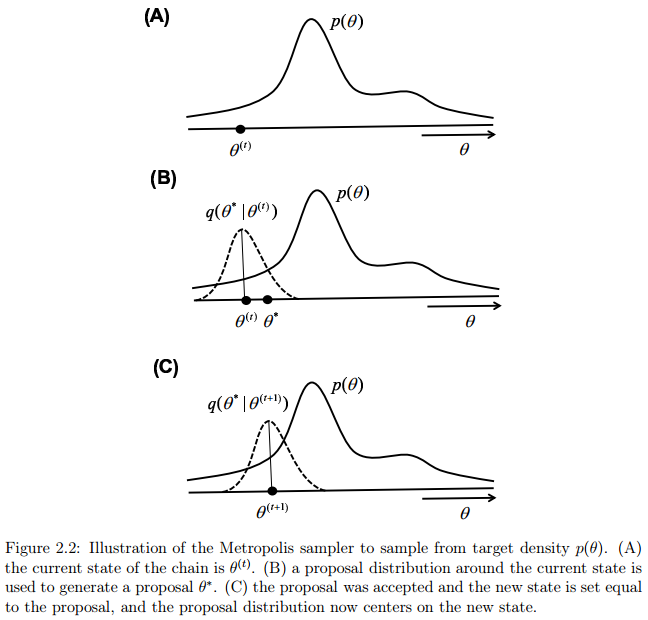
图2.2说明了两个状态序列转移的过程。为了直观地了解该过程为什么能从目标分布中获得样本,注意,如果新的建议分布得到的新状态的建议值相比旧节点状态更有可能在目标分布之下,公式(2.6)将始终接受新的建议。因此,采样器将移动到状态空间中,目标函数密度更高区域。然而,如果新的建议没有当前的状态好,仍然有可能接受这个“更糟糕”的建议并且转移到该建议状态。该过程总是接受“好的”建议,并且偶尔接受“坏的”建议,以确保采样器能探索整个状态空间,并且确保采样的样本从分布的所有部分获得(包含尾部)。
Metropolis sampler一个关键的要求是:建议分布是必须对称的,即: 。因此,基于旧状态到新状态的建议概率,与从新状态返回到旧状态的建议概率是相同的,这样才能满足平稳细致方程(具体细节见:LDA数学八卦, 这里面有非常清晰说明平稳细致方程的含义,下图有个定义)。对称的建议分布有如下:正态分布(Normal),柯西分布(Cauchy),学生t分布(Student-t),以及均匀分布(uniform distributions)。如果建议分布不具有对称性,应该使用Metropolis-Hastings sampler,将在下一节讨论。
图 摘自LDA数学八卦,第31页
Metropolis sampler的主要优点是,公式(2.6)只包含了一个密度函数的比例。因此在函数 中任何独立于 的项都可以被忽略。因此,我们不需要知道密度函数的归一化常量。并且该采样规则允许从非标准分布中采样,这是非常重要的,因为非标准分布在贝叶斯模型中经常用到。
举例
举个例子:假设我们希望从柯西分布中随机采样,给出柯西分布的概率密度如下面公式(2.7):
如何使用Metropolis sampler来模拟这个分布了,采样得到符合这个分布的样本?
答:
因为在Metropolis sampler过程中我们不需要标准化常量,所以将上式重写为公式2.8,:
因此,Metropolis接受概率变为:
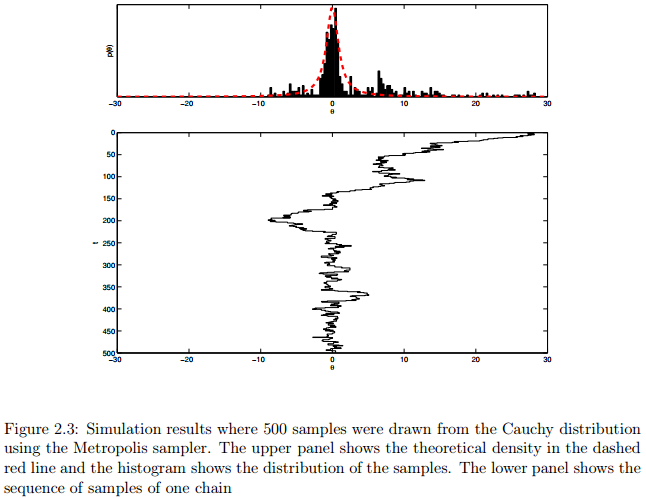
我们使用正态分布作为建议分布,即从 分布中产生建议。因此该分布的均值集中在当前状态,参数 表示标准差需要人为设定,以控制建议分布的可变性。Listing 2.1展示了MATLAB函数,该函数返回非标准的柯西分布的密度。Listing 2.2展示了MATLAB代码实现的Metropolis sampler工具。图2.3展示了单个链经过500次迭代的模拟结果。其中,图2.3的第一个图展示了虚红线的理论密度,直方图展示了500个样本的分布。第二个图展示了样本的一个链。代码很简单,大家可以看看,不懂的可以在评论下方一起讨论。
1 function y = cauchy( theta )
2 %% Returns the unnormalized density of the Cauchy distribution
3 y = 1 ./ (1 + theta.ˆ2);
Listing 2.1: Matlab function to evaluate the unnormalized Cauchy.
1 %% Chapter 2. Use Metropolis procedure to sample from Cauchy density
2
3 %% Initialize the Metropolis sampler
4 T = 500; % Set the maximum number of iterations
5 sigma = 1; % Set standard deviation of normal proposal density
6 thetamin = −30; thetamax = 30; % define a range for starting values
7 theta = zeros( 1 , T ); % Init storage space for our samples
8 seed=1; rand( 'state' , seed ); randn('state',seed ); % set the random seed
9 theta(1) = unifrnd( thetamin , thetamax ); % Generate start value
10
11 %% Start sampling
12 t = 1;
13 while t < T % Iterate until we have T samples
14 t = t + 1;
15 % Propose a new value for theta using a normal proposal density
16 theta star = normrnd( theta(t−1) , sigma );
17 % Calculate the acceptance ratio
18 alpha = min( [ 1 cauchy( theta star ) / cauchy( theta(t−1) ) ] );
19 % Draw a uniform deviate from [ 0 1 ]
20 u = rand;
21 % Do we accept this proposal?
22 if u < alpha
23 theta(t) = theta star; % If so, proposal becomes new state
24 else
25 theta(t) = theta(t−1); % If not, copy old state
26 end
27 end
28
29 %% Display histogram of our samples
30 figure( 1 ); clf;
31 subplot( 3,1,1 );
32 nbins = 200;
33 thetabins = linspace( thetamin , thetamax , nbins );
34 counts = hist( theta , thetabins );
35 bar( thetabins , counts/sum(counts) , 'k' );
36 xlim( [ thetamin thetamax ] );
37 xlabel( '\theta' ); ylabel( 'p(\theta)' );
38
39 %% Overlay the theoretical density
40 y = cauchy( thetabins );
41 hold on;
42 plot( thetabins , y/sum(y) , 'r−−' , 'LineWidth' , 3 );
43 set( gca , 'YTick' , [] );
44
45 %% Display history of our samples
46 subplot( 3,1,2:3 );
47 stairs( theta , 1:T , 'k−' );
48 ylabel( 't' ); xlabel( '\theta' );
49 set( gca , 'YDir' , 'reverse' );
50 xlim( [ thetamin thetamax ] );
Listing 2.2: Matlab code to implement Metropolis sampler for Example 1
2.5 Metropolis-Hastings Sampling
Metropolis-Hasting (MH) sampler是Metropolis sampler的广义版本,我们既可以用对称的分布也可以用不对称的分布作为建议分布。MH sampler的工作方式与Metropolis sampler完全相同,但是使用下列公式计算接受概率:
上式中,MH sampler增加了一个额外的比例公式 。这个增加项可以纠正不对称的建议分布,这样建议分布就可以多种多样了。例如,假设我们有一个以当前状态中心为均值的建议分布,但是该分布是倾斜的。如果该建议分布向左或者向右倾斜,比例公式 将会修正这种不对称。
MH sampler的过程如下:
| 步骤 |
|---|
-
设
-
生成一个初始值 ,并设
-
重复下列过程:
从 中生成一个建议
计算接受该建议的概率
从均匀分布 中生成一个值
如果 ,接受该建议且设置 ;否则设置
- 直到
实际上,不对称建议分布可以在Metropolis Hastings过程中使用,用以从目标分布中采样,这种采样方法也是有限制的。对于一个有界变量,应该在构造合适的建议分布的时候加以考虑。一般地,好的方法是针对目标分布选择具有良好密度函数的建议分布。例如,如果目标分布满足 ,建议分布也应该满足此条件。
2.6 对多变量分布的Metropolis-Hastings
到目前为止,我们讨论的所有的例子都是基于单变量分布的。将MH sampler扩展到多变量分布是非常简单的。有两种不同的方法将采样过程从单个随机变量扩展到多变量空间中。
2.6.1 块更新(Blockwise updating)
第一种方法被称为Blockwise updating,我们使用一个与目标分布相同维度的建议分布。例如,我们想要从一个包含 个变量的概率分布中采样,我们就设计一个 维的建议分布,将建议分布(其中也包含 个变量)作为一个整体,要么接受要么拒绝。接下来,我们使用向量 来表示一个包含 个分量的随机变量,其中 表示采样器的第 状态。用向量代替之前的单个变量,就泛化了MH采样器,过程如下:
| 步骤 |
|---|
-
设
-
生成一个初始值
,并设
-
重复下列过程:
从
中生成一个建议
计算接受该建议的概率
从均匀分布 中生成一个值
如果 ,接受该建议且设置
;否则设置
- 直到
举例
示例1(adopted from Gill, 2008):假设我们想从二元变量空间指数分布中采样:
我们把其中的参数
和
的范围设置为
,并且将其他参数设置如下:
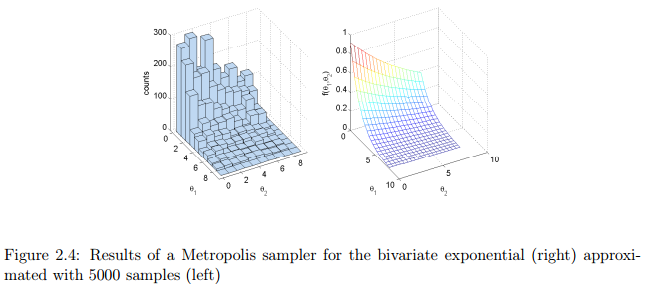
。该二元分布的密度如图2.4(右图)所示。该密度函数的MATLAB实现如Listing 2.3所示。为了解释blockwise MH
sampler,我们使用均匀分布作为建议分布,
和
都从均匀分布
中采样。也就是说,我们从一个盒子中均匀地采样出的建议。注意,用这种特别的建议分布,我们并没有根据前一个状态调整采样器的建议,这就是所谓的独立采样器(independence sampler)。这实际上是一个比较简单的建议分布,但是这也使实现变得简单,因为
,所以这一项在接受概率中消失了。上述这种采样器的MATLAB实现在Listing 2.4中。在Listing 2.4中左图是利用5000个样本模拟的近似分布。
1 function y = bivexp( theta1 , theta2 )
2 %% Returns the density of a bivariate exponential function
3 lambda1 = 0.5; % Set up some constants
4 lambda2 = 0.1;
5 lambda = 0.01;
6 maxval = 8;
7 y = exp( −(lambda1+lambda)*theta1−(lambda2+lambda)*theta2−lambda*maxval );
Listing 2.3: Matlab code to implement bivariate density for Example 1
1 %% Chapter 2. Metropolis procedure to sample from Bivariate Exponential
2 % Blockwise updating. Use a uniform proposal distribution
3
4 %% Initialize the Metropolis sampler
5 T = 5000; % Set the maximum number of iterations
6 thetamin = [ 0 0 ]; % define minimum for theta1 and theta2
7 thetamax = [ 8 8 ]; % define maximum for theta1 and theta2
8 seed=1; rand( 'state' , seed ); randn('state',seed ); % set the random seed
9 theta = zeros( 2 , T ); % Init storage space for our samples
10 theta(1,1) = unifrnd( thetamin(1) , thetamax(1) ); % Start value for theta1
11 theta(2,1) = unifrnd( thetamin(2) , thetamax(2) ); % Start value for theta2
12
13 %% Start sampling
14 t = 1;
15 while t < T % Iterate until we have T samples
16 t = t + 1;
17 % Propose a new value for theta
18 theta star = unifrnd( thetamin , thetamax );
19 pratio = bivexp( theta star(1) , theta star(2) ) / ...
20 bivexp( theta(1,t−1) , theta(2,t−1) );
21 alpha = min( [ 1 pratio ] ); % Calculate the acceptance ratio
22 u = rand; % Draw a uniform deviate from [ 0 1 ]
23 if u < alpha % Do we accept this proposal?
24 theta(:,t) = theta star; % proposal becomes new value for theta
25 else
26 theta(:,t) = theta(:,t−1); % copy old value of theta
27 end
28 end
29
30 %% Display histogram of our samples
31 figure( 1 ); clf;
32 subplot( 1,2,1 );
33 nbins = 10;
34 thetabins1 = linspace( thetamin(1) , thetamax(1) , nbins );
35 thetabins2 = linspace( thetamin(2) , thetamax(2) , nbins );
36 hist3( theta' , 'Edges' , {thetabins1 thetabins2} );
37 xlabel( '\theta 1' ); ylabel('\theta 2' ); zlabel( 'counts' );
38 az = 61; el = 30;
39 view(az, el);
40
41 %% Plot the theoretical density
42 subplot(1,2,2);
43 nbins = 20;
44 thetabins1 = linspace( thetamin(1) , thetamax(1) , nbins );
45 thetabins2 = linspace( thetamin(2) , thetamax(2) , nbins );
46 [ theta1grid , theta2grid ] = meshgrid( thetabins1 , thetabins2 );
47 ygrid = bivexp( theta1grid , theta2grid );
48 mesh( theta1grid , theta2grid , ygrid );
49 xlabel( '\theta 1' ); ylabel('\theta 2' );
50 zlabel( 'f(\theta 1,\theta 2)' );
51 view(az, el);
Listing 2.4: Blockwise Metropolis-Hastings sampler for bivariate exponential distribution
举例
示例2:许多研究者提出概率模型用于解决信息排序问题,排序与很多优先排序问题有关:政治候选人的排名,汽车品牌,冰淇淋口味等。例如,假设要求一个人记住美国历届总统的时间顺序。 Steyvers, Lee, Miller, 和 Hemmer (2009)发现通过简单的概率模型可以捕获这些人在“美国总统排序”问题上犯的很多的错误,如Mallows模型。为了解释Mallows模型,我们先给出一个简单的例子。假设我们先看到五位美国总统是:华盛顿,亚当斯,杰斐逊,麦迪逊和门罗。我们用一个矢量来表示这个真正的顺序
Mallows模型建议需要记住的排序应该是与真正的顺序相似的排序结果,使非常相近的排序比不相似的排序更有可能。具体来说,根据Mallows模型:一个人记住的排序
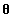
(2.12)
在上式中,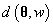

现在的问题是,给定真实序列
和缩放参数
,如何根据Mallows模型生成序列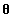
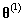
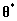
其中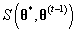
因为建议分布是对称的,所以我们可以使用Metropolis sampler,接受概率是公式(2.14):
Kendall tau distance函数的MATLAB代码实现如Listing 2.5所示。Metropolis sampler的MATLAB代码实现如Listing
2.6所示。简单地展示了在总共500次迭代中每10次迭代的状态。下面是程序的一些示例输出:
1 function tau = kendalltau( order1 , order2 )
2 %% Returns the Kendall tau distance between two orderings
3 % Note: this is not the most efficient implementation
4 [ dummy , ranking1 ] = sort( order1(:)' , 2 , 'ascend' );
5 [ dummy , ranking2 ] = sort( order2(:)' , 2 , 'ascend' );
6 N = length( ranking1 );
7 [ ii , jj ] = meshgrid( 1:N , 1:N );
8 ok = find( jj(:) > ii(:) );
9 ii = ii( ok );
10 jj = jj( ok );
11 nok = length( ok );
12 sign1 = ranking1( jj ) > ranking1( ii );
13 sign2 = ranking2( jj ) > ranking2( ii );
14 tau = sum( sign1 6= sign2 );
Listing 2.5: Function to evaluate Kendall tau distance
1 %% Chapter 2. Metropolis sampler for Mallows model
2 % samples orderings from a distribution over orderings
3
4 %% Initialize model parameters
5 lambda = 0.1; % scaling parameter
6 labels = { 'Washington' , 'Adams' , 'Jefferson' , 'Madison' , 'Monroe' };
7 omega = [ 1 2 3 4 5 ]; % correct ordering
8 L = length( omega ); % number of items in ordering
9
10 %% Initialize the Metropolis sampler
11 T = 500; % Set the maximum number of iterations
12 seed=1; rand( 'state' , seed ); randn('state',seed ); % set the random seed
13 theta = zeros( L , T ); % Init storage space for our samples
14 theta(:,1) = randperm( L ); % Random ordering to start with
15
16 %% Start sampling
17 t = 1;
18 while t < T % Iterate until we have T samples
19 t = t + 1;
20
21 % Our proposal is the last ordering but with two items switched
22 lasttheta = theta(:,t−1); % Get the last theta
23 % Propose two items to switch
24 whswap = randperm( L ); whswap = whswap(1:2);
25 theta star = lasttheta;
26 theta star( whswap(1)) = lasttheta( whswap(2));
27 theta star( whswap(2)) = lasttheta( whswap(1));
28
29 % calculate Kendall tau distances
30 dist1 = kendalltau( theta star , omega );
31 dist2 = kendalltau( lasttheta , omega );
32
33 % Calculate the acceptance ratio
34 pratio = exp( −dist1*lambda ) / exp( −dist2*lambda );
35 alpha = min( [ 1 pratio ] );
36 u = rand; % Draw a uniform deviate from [ 0 1 ]
37 if u < alpha % Do we accept this proposal?
38 theta(:,t) = theta star; % proposal becomes new theta
39 else
40 theta(:,t) = lasttheta; % copy old theta
41 end
42 % Occasionally print the current state
43 if mod( t,10 ) == 0
44 fprintf( 't=%3d\t' , t );
45 for j=1:L
46 fprintf( '%15s' , labels{ theta(j,t)} );
47 end
48 fprintf( '\n' );
49 end
50 end
Listing 2.6: Implementation of Metropolis-Hastings sampler for Mallows model
t=400 Jefferson Madison Adams Monroe Washington
t=410 Washington Monroe Madison Jefferson Adams
t=420 Washington Jefferson Madison Adams Monroe
t=430 Jefferson Monroe Washington Adams Madison
t=440 Washington Madison Monroe Adams Jefferson
t=450 Jefferson Washington Adams Madison Monroe
t=460 Washington Jefferson Adams Madison Monroe
t=470 Monroe Washington Jefferson Adams Madison
t=480 Adams Washington Monroe Jefferson Madison
t=490 Adams Madison Jefferson Monroe Washington
t=500 Monroe Adams Madison Jefferson Washington
2.6.2 Componentwise updating(单变量分别更新)
在blockwise updating更新中存在一个潜在的问题是,可能很难找到一个合适的高纬度建议分布。一个相关的问题是,blockwise updating可以被认为有高的拒绝率。接受或拒绝建议值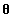
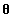
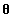
举例
例如,假定我们有一个二元分布 。首先用合适的值初始化采样器的 和 。在第 次迭代中,我们首先根据当前最后一个状态 确定一个建议值 。然后通过比较 和 的相似性估计接受率。注意在该建议中,我们只改变了第一个分量并保持第二个分量不变。 下一步,我们根据当前最后一个状态 确定一个建议 。我们通过比较 和 的相似性估计接受率。重要的是,在第二步我们保持第一个分量不变(该变量是第一步中更新的分量)。因此,第二步中发生的改变是在第一步的条件下发生的。下面是该二元分布进行componentwise MH sampler的过程:
| 步骤 |
|---|
-
设
-
生成一个初始值
,并设
-
重复下列过程:
从
中生成一个建议值
计算接受该建议的概率
从均匀分布 中生成一个值
如果 ,接受该建议并令 ,否则令
从
中生成一个建议
计算接受该建议的概率
从均匀分布 中生成一个值
如果 ,接受该建议并令 ,否则令
- 直到
举例
示例3:我们从多元正态分布中采样,来说明componentwise sampler。首先设置多元正态分布的参数
和
。参数
是一个
的向量,参数
是一个
的协方差矩阵。在本例子中,我们使用二元正态分布,其中
和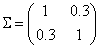
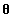
1 %% Chapter 2. Metropolis procedure to sample from Bivariate Normal
2 % Component−wise updating. Use a normal proposal distribution
3
4 %% Parameters of the Bivariate normal
5 mu = [ 0 0 ];
6 sigma = [ 1 0.3; ...
7 0.3 1 ];
8
9 %% Initialize the Metropolis sampler
10 T = 5000; % Set the maximum number of iterations
11 propsigma = 1; % standard dev. of proposal distribution
12 thetamin = [ −3 −3 ]; % define minimum for theta1 and theta2
13 thetamax = [ 3 3 ]; % define maximum for theta1 and theta2
14 seed=1; rand( 'state' , seed ); randn('state',seed ); % set the random seed
15 state = zeros( 2 , T ); % Init storage space for the state of the sampler
16 theta1 = unifrnd( thetamin(1) , thetamax(1) ); % Start value for theta1
17 theta2 = unifrnd( thetamin(2) , thetamax(2) ); % Start value for theta2
18 t = 1; % initialize iteration at 1
19 state(1,t) = theta1; % save the current state
20 state(2,t) = theta2;
21
22 %% Start sampling
23 while t < T % Iterate until we have T samples
24 t = t + 1;
25
26 %% Propose a new value for theta1
27 new theta1 = normrnd( theta1 , propsigma );
28 pratio = mvnpdf( [ new theta1 theta2 ] , mu , sigma ) / ...
29 mvnpdf( [ theta1 theta2 ] , mu , sigma );
30 alpha = min( [ 1 pratio ] ); % Calculate the acceptance ratio
31 u = rand; % Draw a uniform deviate from [ 0 1 ]
32 if u < alpha % Do we accept this proposal?
33 theta1 = new theta1; % proposal becomes new value for theta1
34 end
35
36 %% Propose a new value for theta2
37 new theta2 = normrnd( theta2 , propsigma );
38 pratio = mvnpdf( [ theta1 new theta2 ] , mu , sigma ) / ...
39 mvnpdf( [ theta1 theta2 ] , mu , sigma );
40 alpha = min( [ 1 pratio ] ); % Calculate the acceptance ratio
41 u = rand; % Draw a uniform deviate from [ 0 1 ]
42 if u < alpha % Do we accept this proposal?
43 theta2 = new theta2; % proposal becomes new value for theta2
44 end
45
46 %% Save state
47 state(1,t) = theta1;
48 state(2,t) = theta2;
49 end
50
51 %% Display histogram of our samples
52 figure( 1 ); clf;
53 subplot( 1,2,1 );
54 nbins = 12;
55 thetabins1 = linspace( thetamin(1) , thetamax(1) , nbins );
56 thetabins2 = linspace( thetamin(2) , thetamax(2) , nbins );
57 hist3( state' , 'Edges' , {thetabins1 thetabins2} );
58 xlabel( '\theta 1' ); ylabel('\theta 2' ); zlabel( 'counts' );
59 az = 61; el = 30; view(az, el);
60
61 %% Plot the theoretical density
62 subplot(1,2,2);
63 nbins = 50;
64 thetabins1 = linspace( thetamin(1) , thetamax(1) , nbins );
65 thetabins2 = linspace( thetamin(2) , thetamax(2) , nbins );
66 [ theta1grid , theta2grid ] = meshgrid( thetabins1 , thetabins2 );
67 zgrid = mvnpdf( [ theta1grid(:) theta2grid(:)] , mu , sigma );
68 zgrid = reshape( zgrid , nbins , nbins );
69 surf( theta1grid , theta2grid , zgrid );
70 xlabel( '\theta 1' ); ylabel('\theta 2' );
71 zlabel( 'pdf(\theta 1,\theta 2)' );
72 view(az, el);
73 xlim([thetamin(1) thetamax(1)]); ylim([thetamin(2) thetamax(2)]);
Listing 2.7: Implementation of componentwise Metropolis sampler for bivariate normal
2.7 吉布斯采样(Gibbs Sampling)
Metropolis-Hastings和拒绝采样器的很大的缺点是其很难对于不同的建议分布调参(如何选取最好的建议分布),另外,该方法的一个好处是被拒绝的样本没有用于近似计算中。Gibbs sampler与这些不一样的是:方法采样得到所有的样本都被接受,从而提高了计算效率。另外一个优点是,研究人员不需要指定一个建议分布,这在MCMC过程中留下一些猜想。
然而,Gibbs sampler只能用于我们熟知的情况下,其特点是需要知道所有变量的联合概率分布,比如在多元分布中,我们必须知道每一个变量的联合条件分布,在某些情况下,这些条件分布是未知的,这时就不能使用Gibbs sampling。然而在很多贝叶斯模型中,都可以用Gibbs sampling对多元分布进行采样。
为了解释Gibbs sampler,我们以二元分布的情况为例,其联合分布是 。Gibbs sampler所需要的关键条件是两个条件分布 和 。这两个条件分布表示分布的每个变量都依赖于另一个变量的特定的值实现。同时Gibbs sampler也要求我们可以从这些分布中采样。我们首先用合适的值初始化采样器的 和 。在第 次迭代中,我们要执行的过程与componentwise MH sampler非常相似。第一步,我们首先在 的条件(表示其他部分变量的前一个状态)下采样一个新的值 ,即从条件概率 中采样一个建议值。与Metropolis-Hastings方法相反,我们总是接受当前的建议使新的状态能立即更新。第二步,我们首先在 的条件(表示其他部分变量的前一个状态)下采样一个新的值 ,进行的这一步是基于变量 的条件概率分布 。因此,该采样过程涉及到迭代条件采样(iterative conditional sampling)——我们循环地以当前值以外的其他部分变量为条件采样新的状态,对当前值进行调节。下面是Gibbs sampling的过程:
| 步骤 |
|---|
-
设
-
生成一个初始值
,并设
-
重复下列过程:
*从条件分布 *中采样
从条件分布 中采样
- 直到
举例
示例1:在上一章的“示例3”中,我们利用Metropolis sampler从二元正态分布中采样。二元正态分布也可以用Gibbs sampling进行高效的采样。在二元正态分布中设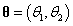
其中包括均值向量和协方差矩阵。本例子中,我们假设协方差矩阵是:
利用解析方法,我们推导出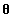
所以,Gibbs sampling的过程如下:
| 步骤 |
|---|
-
设
-
生成一个初始值
,并设
-
重复下列过程:
*从条件分布 *中采样
从条件分布 中采样
- 直到
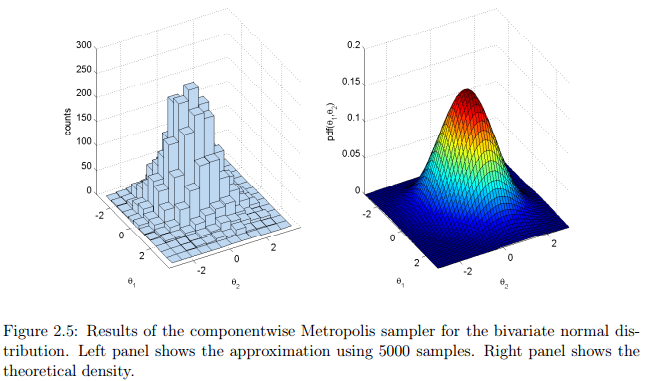
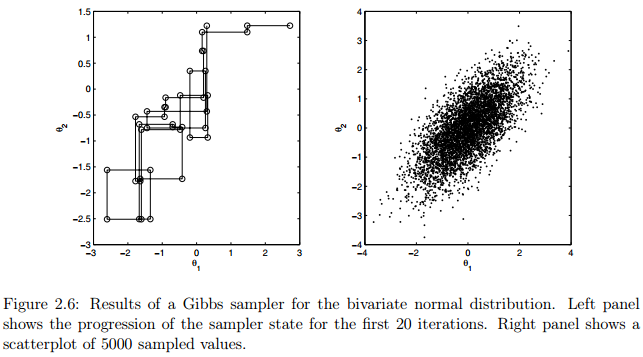
图2.6展示了利用Gibbs sampling二元正态分布的模拟结果,其中和。采样器共在一条链进行5000次迭代。右图展示了所有样本的散点图,左图模拟了前20次迭代的状态的进展。
到目前为止,MCMC这部分的内容翻译完毕,有些名词或者语句由于时间原因有问题,请大家随时提出来,谢谢了。
代码链接: http://pan.baidu.com/s/1qXIWzJu
MCMC matlab tutorial 电子版本:http://pan.baidu.com/s/1i48vyr7
Reference
Mark Steyver. Computational Statistics with Matlab. 2011