化繁为简,一张图看懂梯度、散度、旋度、Jacobian、Hessian和Laplacian
点击上方“计算机视觉life”,选择“星标”
快速获得最新干货
一、入门
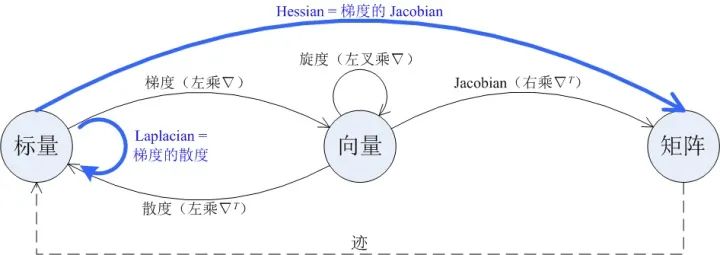
图中的细实线箭头表示了四种一阶微分运算,包括梯度、散度、旋度和 Jacobian。每条箭头的起点表示了相应运算的自变量的类型,终点表示了相应运算的因变量的类型,例如梯度运算是作用在标量上的,结果是向量。图中的「向量」默认为列向量。
这四种一阶微分运算可以统一用算符 (读作 nabla)表示。Nabla 算符是一个形式向量 ,它可以如下地作用于标量 或向量 上:
-
直接与标量 相乘,得到 的梯度 。 -
与向量 点乘,得到 的散度 。本文把点乘用矩阵乘法的形式写作 。 -
与向量 叉乘,得到 的旋度 。 -
若允许偏导算符写在变量的右边,则 就可以表示 的 Jacobian。
图中的粗实线箭头表示了两种二阶微分运算,它们可以由两个一阶微分运算组合而成,即:
-
梯度的散度就是 Laplacian; -
梯度的 Jacobian 就是 Hessian。
图中的虚线箭头表示了一种不涉及微分的运算(迹)。在微分运算之后接上「迹」运算,可能得到另一种微分运算,如:
-
Jacobian 的迹就是散度; -
Hessian 的迹就是 Laplacian。
二、入迷
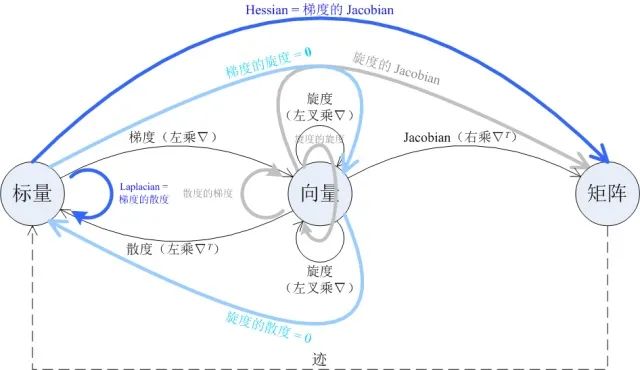
图中的四种一阶微分运算两两搭配,一共可以得到 7 种二阶微分运算。第一节的图中画出了两种,本节的图中画出了另外五种(浅蓝色与灰色)。这五种二阶微分运算并没有特别的名字,但其中有两种是恒等于 0 的:
-
梯度的旋度恒为零向量; -
旋度的散度恒为 0。
其中,「梯度无旋」可以用下面的图形象说明(图片来自@得分的):

如果梯度有旋会怎么样?
三、入魔
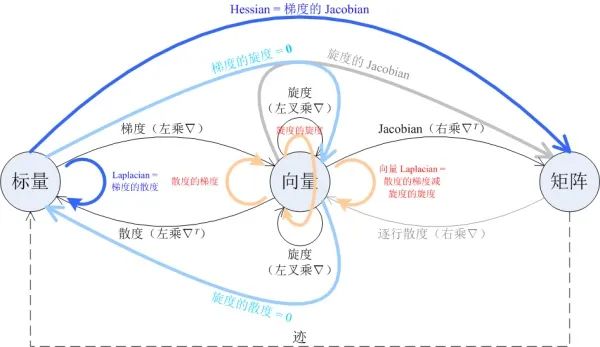
Laplacian 是一个作用于标量的二阶微分运算,其结果也是标量。但我们也可以把它作用于一个向量的每一个元素,得到一个向量;这种运算称为向量 Laplacian。
Laplacian 运算作用于标量 上的结果可以用 nabla 算符写成 。这种写法无法直接推广到向量 Laplacian,因为 里 无法直接跟 做矩阵乘法。但如果允许偏导算符写在变量右边,那就可以把向量 Laplacian 表示成 。这是 Jacobian 运算与「矩阵右乘 」运算的复合;后者的效果是对矩阵的每一行求散度。图中恰好有一个为「逐行散度」运算准备的空位,我们把它补充到图中。
向量 Laplacian 的结果,恰好等于「散度的梯度」与「旋度的旋度」之差。为了体现出这种关系,我把「从向量到向量」的三种二阶微分运算改用橙红色箭头表示。
四、入土
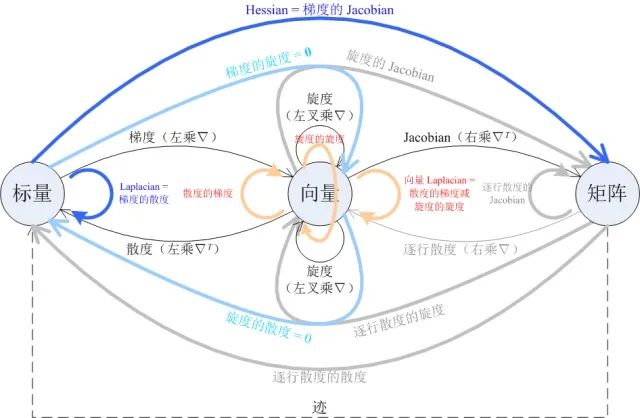
既然引入了「逐行散度」这个一阶微分运算,那就索性把它能组合出来的二阶微分运算也全都放到图里去吧!这样就得到了一个完美对称的图,它包含了 11 种二阶微分运算,其中:
-
有两种比较常见:Laplacian 和 Hessian; -
有两种恒等于零:「梯度的旋度」和「旋度的散度」; -
有三种满足减法关系:向量 Laplacian = 散度的梯度 - 旋度的旋度; -
剩下的四种没有专门的名字,也很罕见。
其中任何一种微分运算后面接上「迹」,都可以得到另一种同阶微分运算:
-
Jacobian 的迹就是散度; -
Hessian 的迹就是 Laplacian; -
旋度的 Jacobian 的迹就是旋度的散度,恒等于 0; -
矩阵逐行散度的 Jacobian 的迹,就是它的逐行散度的散度。
但需要注意只能在运算之后接上「迹」,在运算之前接「迹」是不行的,比如矩阵的迹的梯度不等于它的逐行散度。
如果有读者知道图中几种没有名字的运算叫什么名字、有什么用途,或者在图中内容之外还有什么值得包括进来的微分运算,欢迎补充。
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~
投稿、合作也欢迎联系:simiter@126.com
扫描关注视频号,看最新技术落地及开源方案视频秀 ↓





