从零构建统计随机变量生成器之离散基础篇

2020 年 11 月 23 日 AINLP

本公众号MyEncyclopedia定期发布AI，算法，工程类深度和前沿文章。学习本文的最佳姿势为点击文末在看，发送本文链接到桌面版浏览器，打开文末阅读原文，敲入代码运行。

在本系列中，我们会从第一性原理出发，从零开始构建统计学中的常见分布的随机变量生成器，包括二项分布，泊松分布，高斯分布等。在实现这些基础常见分布的过程中，会展示如何使用统计模拟的通用技术，包括 inverse CDF，Box-Muller，分布转换等。本期通过伯努利试验串联起来基础离散分布并通过代码来实现这些分布的生成函数，从零开始构建的原则是随机变量生成器实现只依赖 random() 产生 [0, 1.0] 之间的浮点数，不依赖于其他第三方API来完成。

均匀分布（离散）

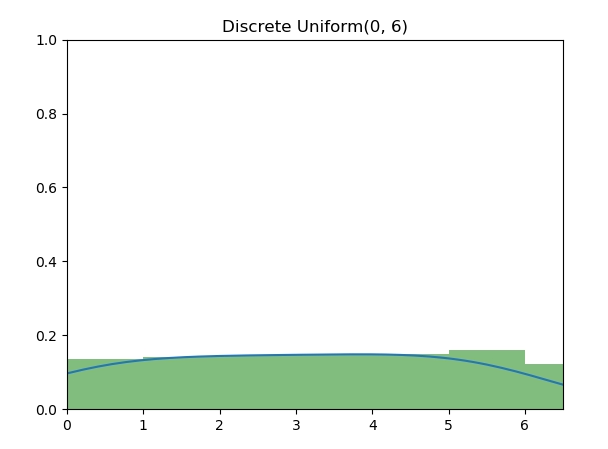
离散均匀分布（Discrete Uniform Distribution）的随机变量是最为基本的，图中为 [0, 6] 七个整数的离散均匀分布。算法实现为，使用 [0, 1] 之间的随机数 u，再将 u 等比例扩展到指定的整数上下界。

实现代码

import random
from math import floor

def uniform(a: int, b: int) -> int:
    assert a <= b
    u = random.random()
    return a + floor((b - a + 1) * u)

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_uniform.py

持续模拟动画

伯努利分布

伯努利分布（Bernoulli Distribution）是support为0或者1的离散分布，0和1可以看成失败和成功两种可能。伯努利分布指定了成功的概率p，例如，下图是 p=0.4 的伯努利分布。

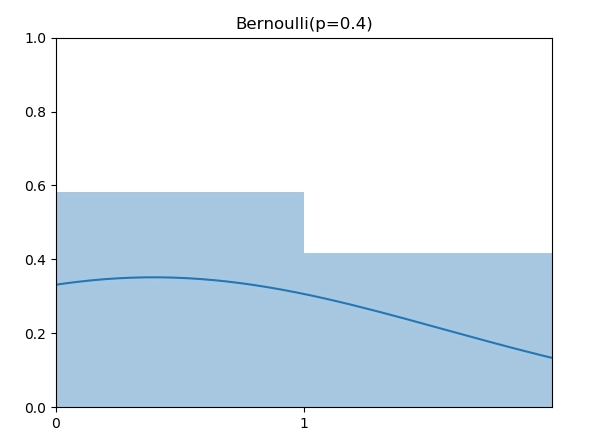
伯努利分布随机数实现也很直接，将随机值 u 根据 p 决定成功或者失败。

实现代码

import random

def bernoulli(p: float) -> int:
    assert 0 <= p <= 1
    u = random.random()
    return 1 if u <= p else 0

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_bernoulli.py

持续模拟动画

类别分布

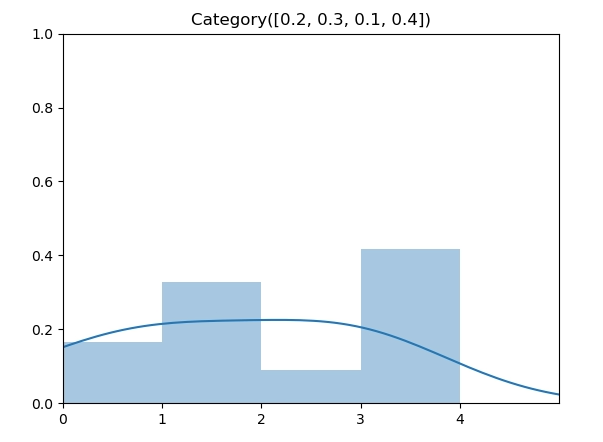
类别分布（Categorical Distribution）是在伯努利分布的基础上扩展到了多个点，每个点同样由参数指定了其概率，因此，其参数从 p 扩展到了向量，如图所示为时的类别分布。

实现代码

类别分布生成函数也扩展了伯努利分布的实现算法，将随机数 u 和累计概率向量作比较。在这个例子中，转换成，再将 u 和数组匹配，返回结果为第一个大于 u 的元素 index。实现上，我们可以以线性复杂度遍历数组，更好一点的方法是，用 python bisect函数通过二分法找到index，将时间复杂度降到。

import bisect
import random
from typing import List

def categorical(probs: List[float]) -> int:
    assert abs(sum(probs) - 1.0) < 0.001
    cum = probs.copy()

    for i in range(1, len(cum)):
        cum[i] = cum[i-1] + probs[i]

    u = random.random()
    return bisect.bisect(cum, u)

Github 代码地址：https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_categorical.py

持续模拟动画

二项分布

二项分布（Binomial Distribution）有两个参数 n 和 p，表示伯努利实验做n次后成功的次数。图中为 n=6，p=0.5的二项分布。

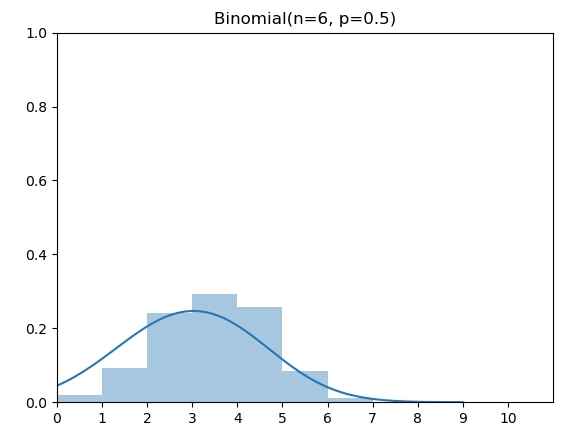
实现代码

二项分布生成算法可以通过伯努利试验的故事来实现，即调用 n 次伯努利分布生成函数，返回总的成功次数。

def binomial(n: int, p: float) -> int:
    return sum(bernoulli(p) for _ in range(n))

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_binomial.py

概率质量函数（PMF）

持续模拟动画

几何分布

几何分布（Geometric Distribution）和伯努利实验的关系是：几何分布是反复伯努利实验直至第一次成功时的失败次数。如图，当成功概率 p=0.4时的几何分布。

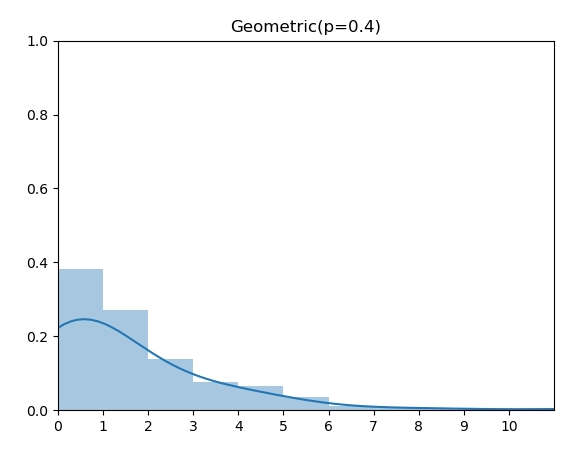
实现代码

from discrete_bernoulli import bernoulli

def geometric(p: float) -> int:
    fail_num = 0
    while not bernoulli(p):
        fail_num += 1
    return fail_num

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_geometric.py

概率质量函数（PMF）

持续模拟动画

负二项分布

负二项分布（Negative Binomial Distribution）是尝试伯努利试验直至成功 r 次的失败次数。

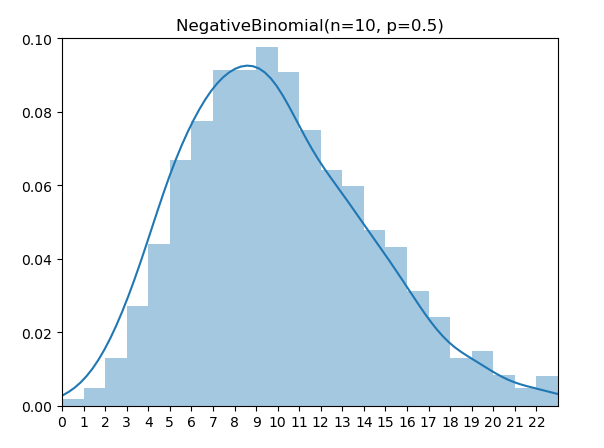
实现代码

from discrete_bernoulli import bernoulli

def negative_binomial(r: int, p: float) -> int:
    failures = 0
    while r:
        success = bernoulli(p)
        if success:
            r -= 1
        else:
            failures += 1
    return failures

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_nagative_binomial.py

概率质量函数（PMF）

持续模拟动画

超几何分布

超几何分布（HyperGeometric Distribution）的意义是从总数为N的集合抽取n次后成功的次数。具体来说，集合由K个表示成功的元素和N-K个表示失败的元素组成，并且抽取时没有替换（without replacement）情况下的成功次数。注意，超几何分布和二项分布的区别仅在于有无替换。

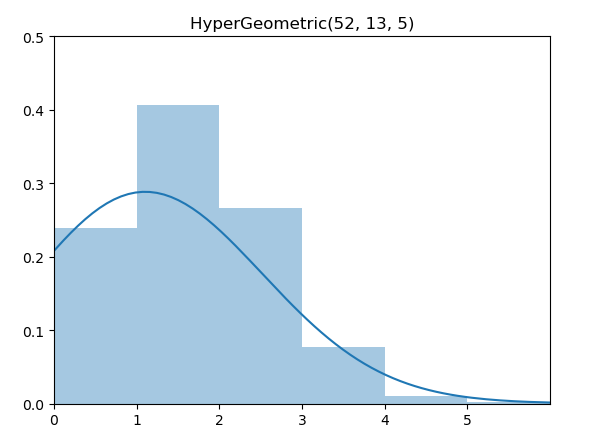
实现代码

from discrete_bernoulli import bernoulli

def hypergeometric(N: int, K_succ_num: int, n_trial_num: int) -> int:
    x = N - K_succ_num
    n_hit = 0
    while n_trial_num:
        hit = bernoulli(K_succ_num / (K_succ_num + x))
        n_hit += hit
        if hit:
            K_succ_num -= 1
        else:
            x -= 1
        if K_succ_num == 0:
            return n_hit
        n_trial_num -= 1
    return n_hit

Github 代码地址：

https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_hypergeometric.py

概率质量函数（PMF）

持续模拟动画

负超几何分布

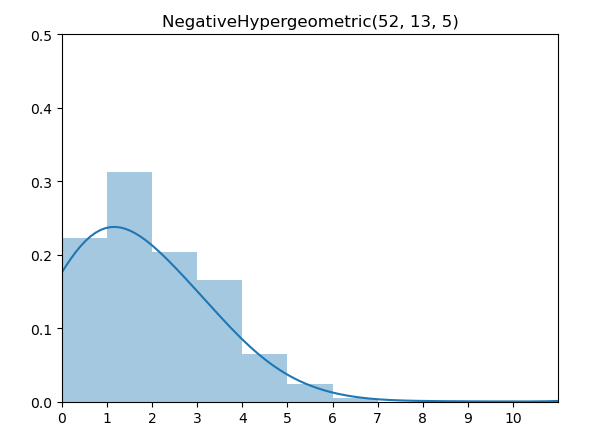
负超几何分布（Negative Hypergeometric Distribution）的意义是从总数为N的集合中，无替换下抽取直至 r 次失败时，成功的次数。

实现代码

from discrete_bernoulli import bernoulli

def negative_hypergeometric(N: int, K_success_num: int, r_fail_times: int) -> int:
    fail_num = N - K_success_num
    succ_trials = 0
    while r_fail_times:
        success = bernoulli(K_success_num / (K_success_num + fail_num))
        if success:
            K_success_num -= 1
            succ_trials += 1
            if K_success_num == 0: # no more success elements
                return succ_trials
        else:
            fail_num -= 1
            r_fail_times -= 1
    return succ_trials

Github 代码地址：https://github.com/MyEncyclopedia/stats_simulation/blob/main/distrib_sim/discrete_negative_hypergeometric.py

概率质量函数（PMF）

持续模拟动画

伯努利试验总结

下表总结了上面四种和伯努利试验有关的离散分布的具体区别。

	有替换	无替换
固定尝试次数	二项 Binomial	超几何 Hypergeometric
固定成功次数	负二项 Negative Binomial	负超几何 Negative Hypergeometric

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方"AINLP"，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。