The Mechanics of CNN Filtering with Rectification

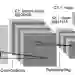
This paper proposes elementary information mechanics as a new model for understanding the mechanical properties of convolutional filtering with rectification, inspired by physical theories of special relativity and quantum mechanics. We consider kernels decomposed into orthogonal even and odd components. Even components cause image content to diffuse isotropically while preserving the center of mass, analogously to rest or potential energy with zero net momentum. Odd kernels cause directional displacement of the center of mass, analogously to kinetic energy with non-zero momentum. The speed of information displacement is linearly related to the ratio of odd vs total kernel energy. Even-Odd properties are analyzed in the spectral domain via the discrete cosine transform (DCT), where the structure of small convolutional filters (e.g. $3 \times 3$ pixels) is dominated by low-frequency bases, specifically the DC $Σ$ and gradient components $\nabla$, which define the fundamental modes of information propagation. To our knowledge, this is the first work demonstrating the link between information processing in generic CNNs and the energy-momentum relation, a cornerstone of modern relativistic physics.