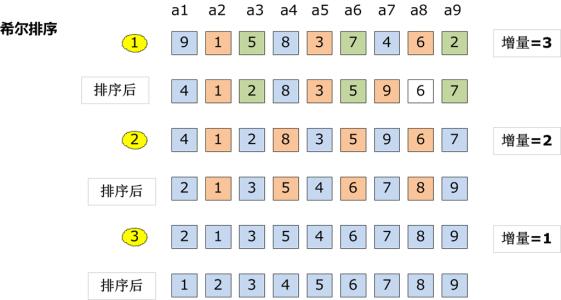
When using graphs and graph transformations to model systems, consistency is an important concern. While consistency has primarily been viewed as a binary property, i.e., a graph is consistent or inconsistent with respect to a set of constraints, recent work has presented an approach to consistency as a graduated property. This allows living with inconsistencies for a while and repairing them when necessary. For repairing inconsistencies in a graph, we use graph transformation rules with so-called {\em impairment-indicating and repair-indicating application conditions} to understand how much repair gain certain rule applications would bring. Both types of conditions can be derived from given graph constraints. Our main theorem shows that the difference between the number of actual constraint violations before and after a graph transformation step can be characterised by the difference between the numbers of violated impairment-indicating and repair-indicating application conditions. This theory forms the basis for algorithms with look-ahead that rank graph transformations according to their potential for graph repair. An evaluation shows that graph repair can be well-supported by rules with these new types of application conditions in terms of effectiveness and scalability.
翻译:在使用图和图转换对系统进行建模时,一致性是一个重要问题。尽管一致性通常被视为二元属性,即图相对于一组约束要么一致要么不一致,但近期研究提出了一种将一致性视为渐进属性的方法。这使得系统可以暂时容忍不一致性,并在必要时进行修复。为了修复图中的不一致性,我们采用具有所谓“损害指示与修复指示应用条件”的图转换规则,以评估特定规则应用能带来多大的修复收益。这两类条件均可从给定的图约束中推导得出。我们的主要定理表明,图转换步骤前后实际约束违反数量的差异,可通过违反的损害指示条件与修复指示条件数量之差来表征。该理论构成了具有前瞻性算法的基础,这些算法根据图转换在图修复中的潜力对其进行排序。评估结果表明,在有效性和可扩展性方面,配备这些新型应用条件的规则能很好地支持图修复。