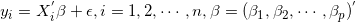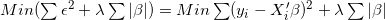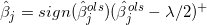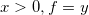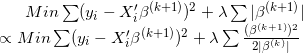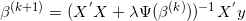数据分析师应该知道的16种回归技术:Lasso回归
岭回归通过添加L2损失函数收缩回归系数,使回归系数的估计值更加稳定,但它不能把任意回归系数收缩到0,因此不能用来进行变量选择,从而不能给出一个易于解释的模型(对于具体的多变量数据,我们总希望通过尽量少的变量描述数据的特征)。今天学习的lasso(least absolute shrinkage and selection operator)可以很好地解决这个问题
Lasso回归的目标函数和岭回归类似,只不过把岭回归中的L2损失函数替换为L1损失函数,于是对于下列回归模型:
Lasso回归的目标函数为
上述目标函数的解析解,除非
若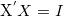
这里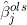
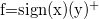
若
然后带入lasso的目标函数,可得
解上述目标函数,可得
其中
上述迭代过程将收敛到lasso的估计值,另外对于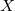
最后一个问题是设置参数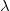
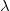
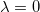
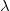
案例
前列腺癌是一种恶性男科病,PSA(某种前列腺抗原)数是用来判断病人是否患前列腺癌的重要指标。现有一批PSA诊断数据,包含8项诊断指标。我们希望用尽量少的指标来预测病人的PSA数量,进而判断病人是否得了前列腺癌。
下面我们采用LASSO回归来分析PSA数据
对于PSA数据,利用交叉验证寻找最优lambda,然后求解最优lambda下的回归系数
data(Prostate, package = 'lasso2')
x<-(apply(Prostate[,-9],2,as.numeric))
y<-(Prostate[,9])
library(glmnet)
set.seed(123)
model <- cv.glmnet(x, y,lambda = 10^seq(4,-1,-0.1),keep = T)
best_lambda <- model$lambda.min
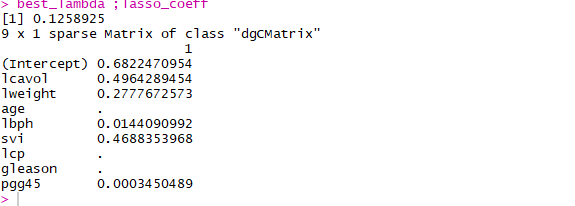
lasso_coeff <- predict(model,s = best_lambda,type = "coefficients")
best_lambda ;lasso_coeff
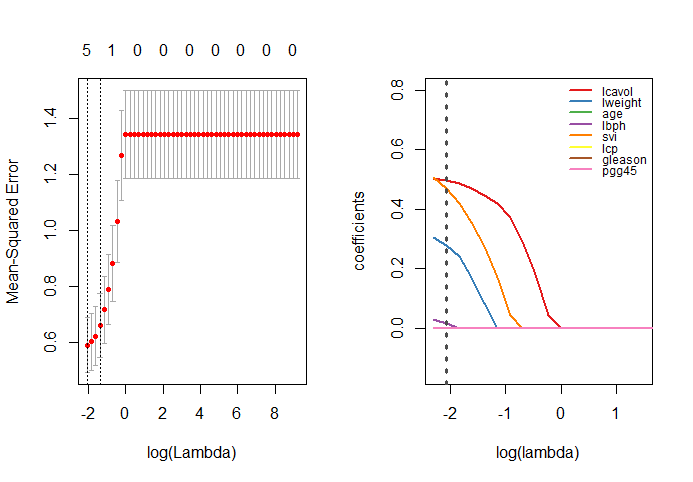
绘制不同lambda下回归系数的变化曲线,以及MSE的变化情况。
op=par(mfrow=c(1,2))
plot(model)
hatbeta <- as.matrix(model$glmnet.fit$beta)
lambda = log(10^seq(4,-1,-0.1))
plot(1,type = 'n',xlim = c(-2.3,1.5),ylim = c(-0.15,0.8),
xlab = 'log(lambda)',ylab = 'coefficients')
colrs = RColorBrewer::brewer.pal(8,"Set1")
for (i in 1:8) {
lines(lambda,hatbeta[i,],col=colrs[i],lwd=2)
}
abline(v=log(best_lambda),lty=3,lwd=3,col='gray30')
legend('topright',rownames(hatbeta),lty = 1,lwd=2,
col=colrs,bty = 'n',cex = 0.75)
par(op)
推荐阅读
从零开始深度学习第8讲:利用Tensorflow搭建神经网络

长按二维码关注“数萃大数据”