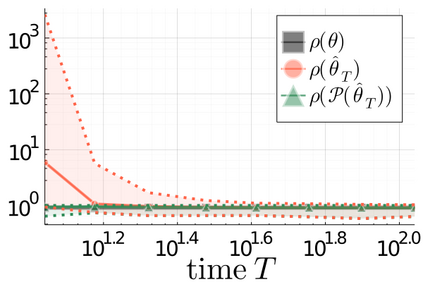
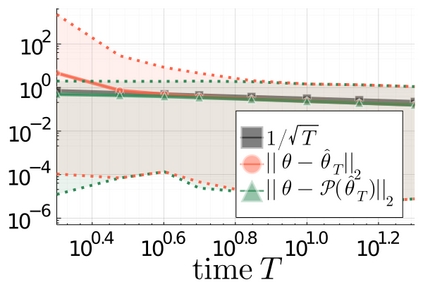
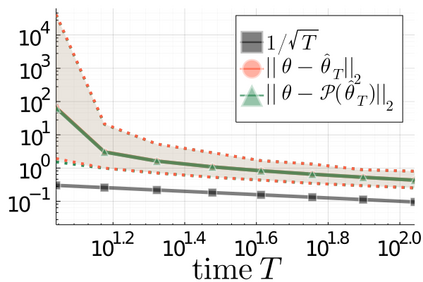
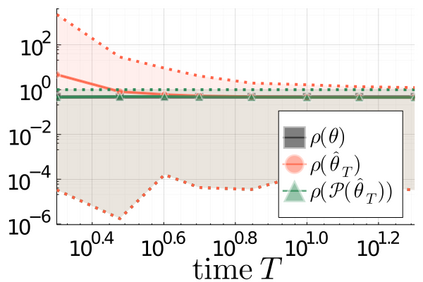
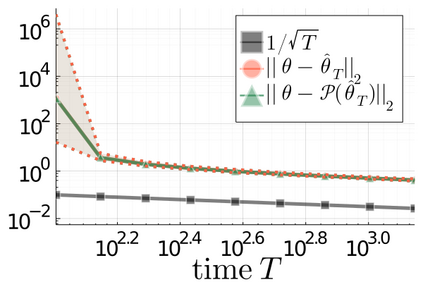
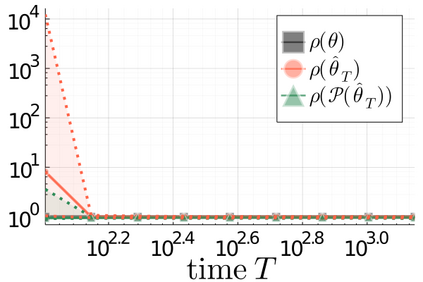
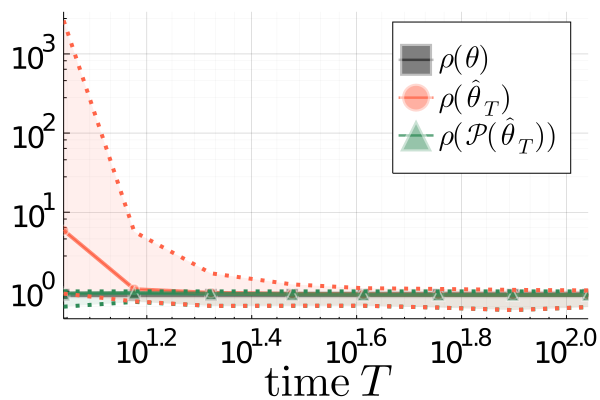
We propose a principled method for projecting an arbitrary square matrix to the non-convex set of asymptotically stable matrices. Leveraging ideas from large deviations theory, we show that this projection is optimal in an information-theoretic sense and that it simply amounts to shifting the initial matrix by an optimal linear quadratic feedback gain, which can be computed exactly and highly efficiently by solving a standard linear quadratic regulator problem. The proposed approach allows us to learn the system matrix of a stable linear dynamical system from a single trajectory of correlated state observations. The resulting estimator is guaranteed to be stable and offers explicit statistical bounds on the estimation error.
翻译:我们提出一种原则性方法,将任意的平方矩阵投射到非冷凝的无症状稳定的矩阵中。 利用大偏差理论的想法,我们表明这一预测在信息理论意义上是最佳的,它仅仅相当于将初始矩阵转换为最佳线性二次反馈收益,可以通过解决标准的线性二次调节问题来准确和高效地计算。 拟议的方法使我们能够从相关国家观测的单一轨迹中学习稳定的线性动态系统的系统矩阵。 由此得出的估计值将保证稳定,并为估算错误提供明确的统计界限。