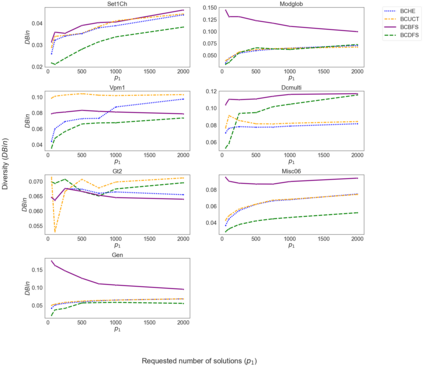
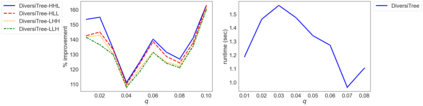
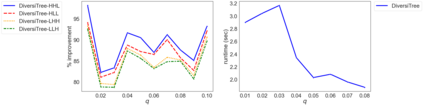
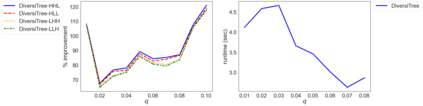
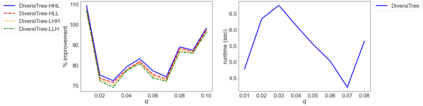
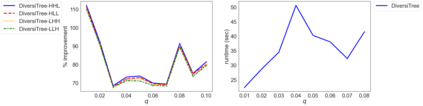
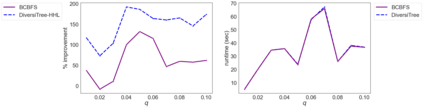
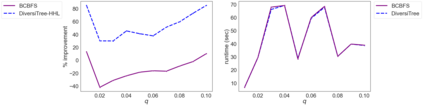
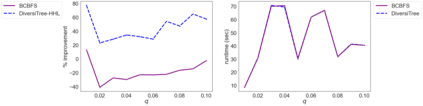
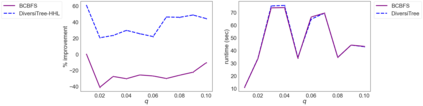
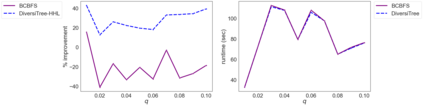
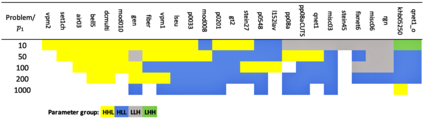
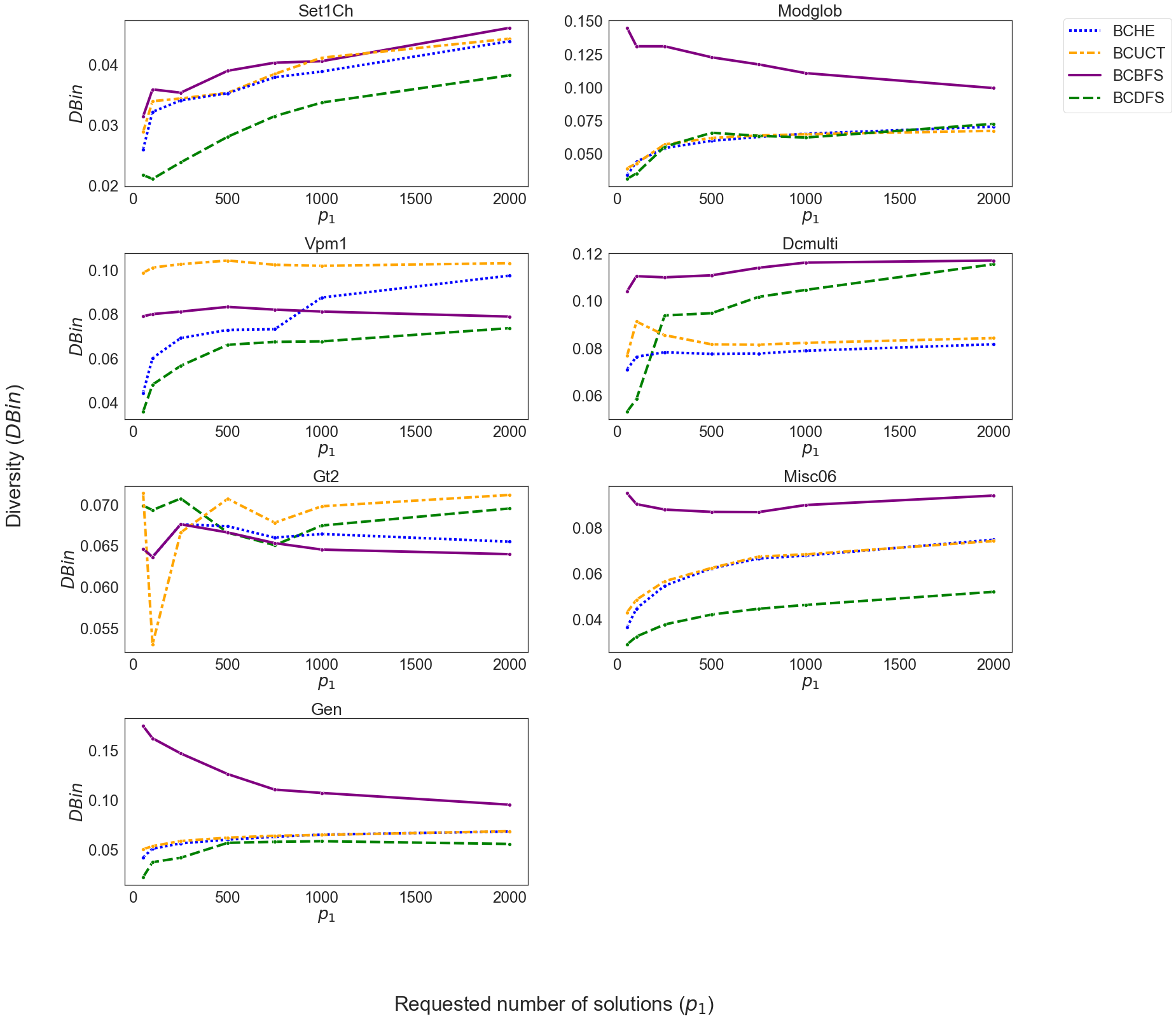
While most methods for solving mixed-integer optimization problems compute a single optimal solution, a diverse set of near-optimal solutions can often lead to improved outcomes. We present a new method for finding a set of diverse solutions by emphasizing diversity within the search for near-optimal solutions. Specifically, within a branch-and-bound framework, we investigated parameterized node selection rules that explicitly consider diversity. Our results indicate that our approach significantly increases the diversity of the final solution set. When compared with two existing methods, our method runs with similar runtime as regular node selection methods and gives a diversity improvement between 12% and 190%. In contrast, popular node selection rules, such as best-first search, in some instances performed worse than state-of-the-art methods by more than 35% and gave an improvement of no more than 130%. Further, we find that our method is most effective when diversity in node selection is continuously emphasized after reaching a minimal depth in the tree and when the solution set has grown sufficiently large. Our method can be easily incorporated into integer programming solvers and has the potential to significantly increase the diversity of solution sets.
翻译:虽然解决混合整数优化问题的大多数方法都计算出一种单一的最佳解决办法,但一套多样化的近乎最佳的解决方案往往会导致更好的结果。 我们提出了一个新方法,通过在寻找近于最佳的解决办法时强调多样性来寻找一套不同的解决方案。 具体地说,在分支和约束的框架内,我们调查了明确考虑多样性的参数化节点选择规则。 我们的结果表明,我们的方法大大增加了最终解决办法的多样性。 与两种现有方法相比,我们的方法运行的时间与常规节点选择方法相似,使多样性在12%至190 % 之间得到改进。 相比之下,流行节点选择规则,例如最佳第一搜索,在某些情况下比最新方法差35%以上,改进不到130 %。 此外,我们发现,当节点选择的多样性在树上达到最低限度的深度之后,当解决方案已经发展得足够大时,我们的方法最为有效。 我们的方法可以很容易地融入整数编程方案解决器,并有可能大大增加解决方案的多样化。