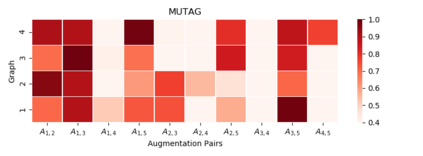
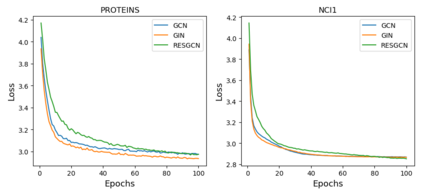
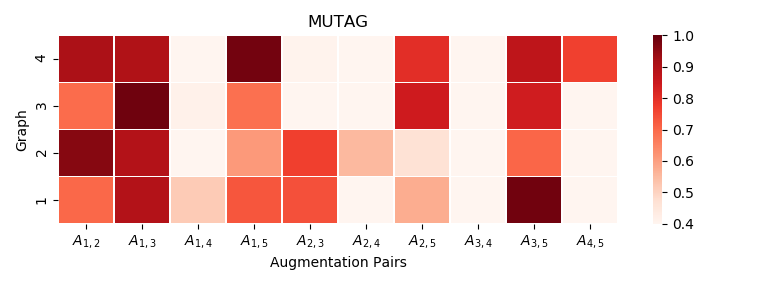
Graph Contrastive Learning with Personalized Augmentation

Graph contrastive learning (GCL) has emerged as an effective tool for learning unsupervised representations of graphs. The key idea is to maximize the agreement between two augmented views of each graph via data augmentation. Existing GCL models mainly focus on applying \textit{identical augmentation strategies} for all graphs within a given scenario. However, real-world graphs are often not monomorphic but abstractions of diverse natures. Even within the same scenario (e.g., macromolecules and online communities), different graphs might need diverse augmentations to perform effective GCL. Thus, blindly augmenting all graphs without considering their individual characteristics may undermine the performance of GCL arts.To deal with this, we propose the first principled framework, termed as \textit{G}raph contrastive learning with \textit{P}ersonalized \textit{A}ugmentation (GPA), to advance conventional GCL by allowing each graph to choose its own suitable augmentation operations.In essence, GPA infers tailored augmentation strategies for each graph based on its topology and node attributes via a learnable augmentation selector, which is a plug-and-play module and can be effectively trained with downstream GCL models end-to-end. Extensive experiments across 11 benchmark graphs from different types and domains demonstrate the superiority of GPA against state-of-the-art competitors.Moreover, by visualizing the learned augmentation distributions across different types of datasets, we show that GPA can effectively identify the most suitable augmentations for each graph based on its characteristics.