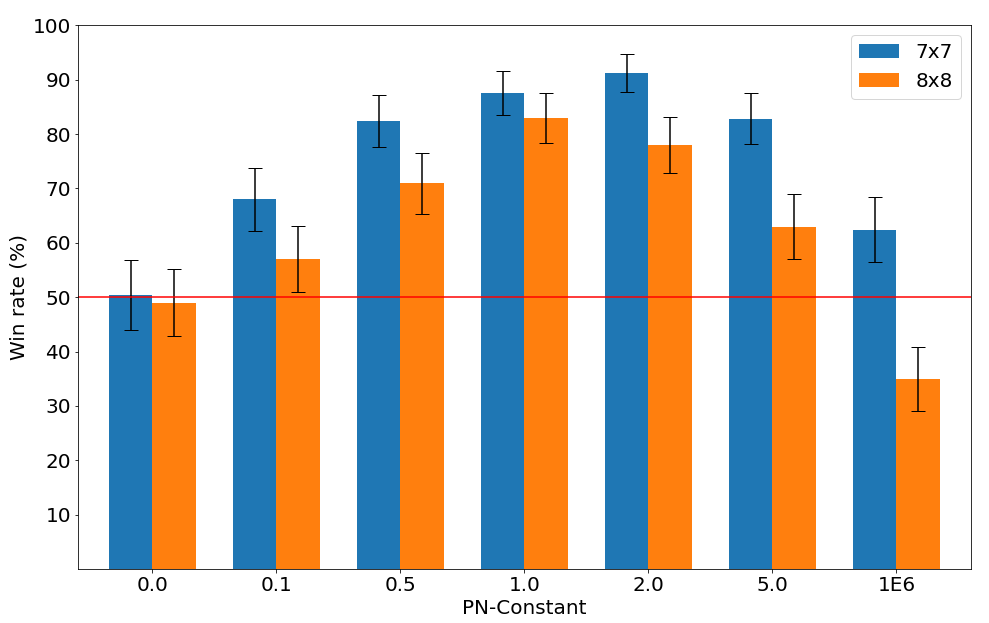
This paper proposes a new game search algorithm, PN-MCTS, that combines Monte-Carlo Tree Search (MCTS) and Proof-Number Search (PNS). These two algorithms have been successfully applied for decision making in a range of domains. We define three areas where the additional knowledge provided by the proof and disproof numbers gathered in MCTS trees might be used: final move selection, solving subtrees, and the UCT formula. We test all possible combinations on different time settings, playing against vanilla UCT MCTS on several games: Lines of Action ($7$$\times$$7$ and $8$$\times$$8$), MiniShogi, Knightthrough, Awari, and Gomoku. Furthermore, we extend this new algorithm to properly address games with draws, like Awari, by adding an additional layer of PNS on top of the MCTS tree. The experiments show that PN-MCTS confidently outperforms MCTS in 5 out of 6 game domains (all except Gomoku), achieving win rates up to 96.2% for Lines of Action.
翻译:本文提出一个新的游戏搜索算法,即PN-MCTS,将蒙特-卡洛树搜索(MCTS)和校对数搜索(PNS)结合起来。这两种算法已经成功地应用于一系列领域的决策。我们定义了三个领域,其中可以利用在MCTS树中收集的校对和无节制数字提供的额外知识:最后的移动选择、解决亚树和UCT公式。我们在不同的时间设置上测试所有可能的组合,在几个游戏中与Vanilla UCT MCTTS比赛:行动线(7美元/乘数$7美元和8美元/乘数$8美元)、MiniShogi、Knightlough、Awari和Gomoko。此外,我们扩大这种新的算法,在像Awari那样的绘图上加上一个额外的PNS层。实验显示,PN-MCTS在6个游戏域中的5个域(除Gomoku外),赢得96.2%的得分数。</s>