算法和数据驱动的决策和建议通常用于刑事司法、医学和公共政策等高风险决策环境中。我们利用 1969 年底推出的安全评估算法后立即测量的结果,研究是否有可能改进该算法。这一实证应用提出了在高风险算法决策中经常出现的几个方法论挑战。首先,在实施新算法之前,必须确定并控制产生比现有算法更差结果的风险。其次,现有算法是确定性的,学习新算法需要透明的外推法。第三,现有算法涉及离散决策表,这些决策表很常见,但很难优化。
为了应对这些挑战,我们引入了平均条件风险 (ACRisk),它首先量化了新算法政策导致个体单位子群结果变差的风险,然后将其平均到子群分布上。我们还提出了一个贝叶斯政策学习框架,在控制后验预期 ACRisk 的同时,最大化后验预期值。这一框架将异质性治疗效果的估计与政策优化分离开来,实现了对效果的灵活估计和对复杂政策类别的优化。我们将由此产生的机会受限优化问题描述为受限线性规划问题。我们的分析表明,与越战期间使用的实际算法相比,学习算法将大多数地区评估为更安全的地区,并强调经济和政治因素而非军事因素。
引言
算法和数据驱动的决策与建议早已应用于信贷市场(Lauer,2017 年)和战争(Daddis,2012 年)等不同领域。现在,它们越来越成为当今社会许多方面不可或缺的一部分,包括在线广告(如 Li 等人,2010 年;Tang 等人,2013 年;Schwartz 等人,2017 年)、医疗(如 Kamath 等人,2001 年;Nahum-Shani 等人,2018 年)和刑事司法(如 Imai 等人,2023 年;Greiner 等人,2020 年)。将数据驱动政策应用于重大决策任务时,面临的一个主要挑战是如何描述和控制从数据中学到的任何新政策的相关风险。医学、公共政策和军事等领域的利益相关者可能会担心,采用新的数据衍生政策可能会无意中导致某些人在某些情况下出现更糟糕的结果。
在本文中,我们考虑了一个特别高风险的环境,分析了在越南战争中使用的美国军事安全评估政策。战争期间,美国军方开发了一种名为 "哈姆雷特评估系统"(Hamlet Evaluation System,HES)的数据驱动评分系统,为每个地区得出一个安全分数(PACAF,1969 年);指挥官利用这些分数做出空袭决定。最近一项基于回归不连续设计的分析表明,空袭对包括地区安全、经济和公民社会措施在内的发展成果产生了显著的负面影响,因此在很大程度上适得其反(Dell 和 Querubin,2018 年)。我们考虑是否有可能利用美国军方和相关机构收集的同期数据来改进 HES,以反映这一事实,同时通过改变评估系统来避免许多地区发展成果恶化的风险。
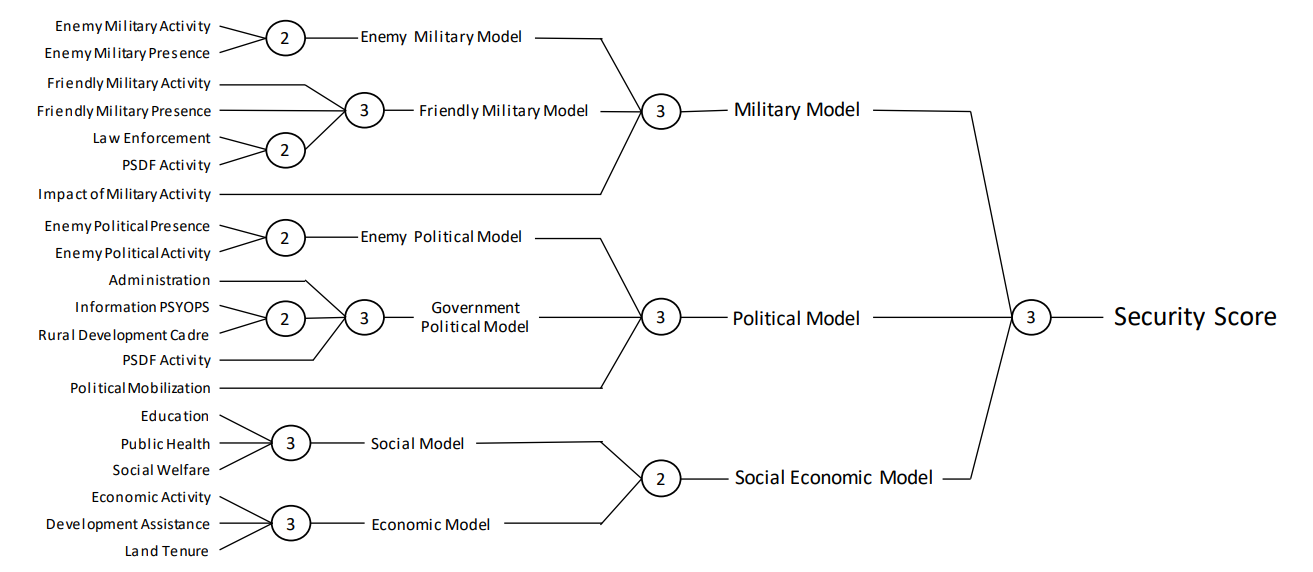
特别是,最初的 HES 是由各种 "子模型分数 "组成的,这些分数根据调查反馈来衡量每个地区的不同方面(如经济变量、地方行政管理、敌方军事存在)。然后,该系统通过使用预定义决策表确定如何合并不同分数的三级分层汇总方法,将这些分数合并为一个单一的安全分数。然后将安全分数提交给空军指挥官,由他们做出目标选择决策。因此,我们的目标是通过改变基本决策表来修改 HES,找到能优化各种发展目标的决策表,同时限制个别地区这些目标恶化的风险。
这一经验性问题提出了几个在高风险数据驱动决策环境中通常会遇到的方法论挑战。首先,我们希望描述和控制新的决策、分类或建议政策可能导致某些地区组(即单个单位)结果恶化的风险。其次,HES 是输入数据的确定性函数,这意味着要学习新政策,就必须进行外推。第三,安全得分是通过使用决策表进行一系列汇总而得出的。事实上,决策表在许多公共政策和医疗决策环境中都得到了广泛应用(例如,美国刑事司法系统中的风险评分 Greiner 等人,2020 年;Imai 等人,2023 年),但在实践中对其进行优化却具有挑战性。
为了应对这些挑战,我们引入了一种风险度量--平均条件风险(ACRisk),它首先量化了特定政策对具有一组特定协变量的个体单位群体的风险,然后将这种条件风险平均到协变量的分布上。与描述政策平均绩效不确定性的现有风险度量(如 Delage 和 Mannor,2010 年;Vakili 和 Zhao,2015 年;Bai 等人,2022 年)不同,ACRisk 度量的是所学政策对子群产生负面影响的程度。这使我们能够更好地描述应用新政策的潜在异质性风险。
有了这个风险度量指标,我们提出了一个贝叶斯安全政策学习框架,在控制后验预期 ACR 风险的同时,最大化观测数据的后验预期值。我们将其表述为一个机会受限的优化问题,并展示了如何利用条件平均治疗效果(CATE)的后验分布样本高效地解决该问题。
拟议框架的主要优势在于其灵活性。由于偶然性约束优化问题只依赖于后验样本,因此可以使用流行的贝叶斯非参数回归模型,如 BART 和高斯过程回归(Rasmussen 和 Williams,2006 年;Chipman 等人,2010 年;Branson 等人,2019 年),同时在复杂的政策类别中高效地找到最优政策。这对于像我们这种协变量重叠有限或没有协变量重叠的情况尤其有帮助,我们的框架允许通过贝叶斯先验进行灵活的外推。相比之下,频数主义的安全政策学习概念依赖于稳健优化,需要解决潜在模型类和潜在政策类的最小优化问题,因此很难同时考虑非参数模型和复杂政策类(Pu 和 Zhang,2020 年;Kallus 和 Zhou,2021 年;Ben-Michael 等,2022 年;Zhang 等,2022 年)。
我们通过模拟研究表明,控制后预期 ACR 风险可有效限制各种情况下的 ACR 风险,降低损害某些单位子群的风险。我们还发现,尽管所提出的方法设计得比较保守,但在某些信噪比较低的情况下,它所产生的新政策的平均值要高于没有安全约束的政策。这证明所提出的安全约束能有效地规范政策优化问题。
在我们的实证分析中,我们应用所提出的方法来寻找对 HES 的调整,以获得更好的总体结果(以军事、经济和社会目标为衡量标准),同时限制某些地区在新系统下的结果比在原始 HES 下更差的后验概率。我们考虑了两个政策学习问题--一个是我们只改变分层汇总最后一层中使用的决策表,另一个是我们同时修改所有三层分层汇总中使用的决策表。为了处理后一种复杂情况,我们开发了一种基于有向无环图分区随机行走的随机优化算法,该算法普遍适用于决策表。我们的分析一致表明,原始的 HES 过于悲观--将地区评估得过于不安全--并且过于强调军事因素,而对 HES 进行的数据化调整则将地区评估得更为安全,并更多地依赖经济和社会因素来得出地区安全分数。
文献综述
近年来,统计学家和机器学习研究人员对从随机实验和观察研究中寻找最优政策的兴趣与日俱增(例如,Beygelzimer 和 Langford, 2009; Qian 和 Murphy, 2011; Dud´ık et al、 2011;Zhao 等人,2012;Zhang 等人,2012;Swaminathan 和 Joachims,2015;Luedtke 和 Van Der Laan,2016;Zhou 等人,2017;Kitagawa 和 Tetenov,2018;Kallus,2018;Athey 和 Wager,2021;Zhou 等人,2022)。这些研究通常在频繁主义框架下考虑以下两个步骤--首先通过 CATE 确定给定政策的平均性能或价值,然后根据观察到的数据,通过最大化估计值来学习最优政策
与此相反,我们采用贝叶斯视角--首先根据观察到的数据获得 CATE 的后验分布,然后通过最大化后验期望值来学习最优政策。贝叶斯方法已被广泛用于因果推理(近期综述见 Li 等人,2022b)。特别是,BART 和高斯过程经常被用来灵活估计 CATE(Hill,2011 年;Branson 等人,2019 年;Taddy 等人,2016 年;Hahn 等人,2020 年)。然而,贝叶斯方法似乎很少应用于政策学习。我们提出的框架利用了这些流行的贝叶斯非参数方法来实现安全的政策学习。
关于在无法识别 CATE 的情况下进行政策学习的文献也在不断增加。这些文献包括带有未测量混杂因素的观察研究(Kallus 和 Zhou,2021 年)、带有不遵守或工具变量的研究(Pu 和 Zhang,2020 年)、由于确定性治疗规则而缺乏重叠的研究(Ben-Michael 等,2021 年;Zhang 等,2022 年)以及涉及潜在结果联合集的效用函数(Ben-Michael 等,2022 年)。这些研究首先部分确定了给定政策的价值,然后通过稳健优化找到使最坏情况价值最大化的政策。我们的方法与之不同,我们只依靠后验样本进行政策学习,从而将估计与政策优化分离开来。
在强化学习(RL)文献中,人们以不同的名称研究了各种安全概念(如安全强化学习、风险规避强化学习、悲观强化学习;见 Garcıa 和 Fernandez ´ (2015))。例如,Geibel 和 Wysotzki(2005 年)在寻找最优策略时,通过明确施加风险约束来控制代理访问 "危险状态 "的风险。相比之下,Sato 等人(2001 年)和 Vakili 和 Zhao(2015 年)在寻找高预期收益和低方差的最优政策时,将收益方差作为目标中的惩罚项。这些 RL 文献主要关注在线环境,在在线环境中,算法的设计是为了避免探索过程中的风险,而我们研究的是在离线环境中应用数据驱动策略的风险。
我们还扩展了现有工作,提出了 ACRisk 概念,并将其作为优化新策略后验预期值的约束条件。相关文献是悲观离线 RL,它使用值的置信下限(LCB)来量化给定策略的风险,并找到一个具有最佳 LCB 的策略(Jin 等人,2021 年;Buckman 等人,2020 年;Zanette 等人,2020 年)、 2020;Zanette 等人,2021;Xie 等人,2021;Chen 和 Jiang,2022;Rashidinejad 等人,2021;Yin 和 Wang,2021;Shi 等人,2022;Yan 等人,2022;Uehara 和 Sun,2021;Bai 等人,2022;Jin 等人,2022)。相比之下,拟议的 ACR 风险衡量的是与基线政策相比,新政策对某些群体产生负面影响的程度。
最后,我们的工作还与机会约束优化有关,后者被广泛应用于不确定性下的决策分析(例如,Schwarm 和 Nikolaou,1999 年;Filar 等人,1995 年;Delage 和 Mannor,2007 年、2010 年;Farina 等人,2016 年)。例如,Delage 和 Mannor(2010 年)考虑了马尔可夫决策过程的机会约束控制。他们假定奖励分布为高斯模型,并使用机会约束优化来找到一种能以高后验概率实现低遗憾的策略。我们的方法考虑了高斯模型之外的更一般的设置,并使用 ACRisk 的后验期望值作为约束,这与现有的工作有所不同。
提纲
本文的其余部分安排如下。第 2 节介绍了美国在越南战争中的军事安全评估、HES 以及相关的经验政策学习问题。第 3 节介绍了正式设置,第 4 节介绍了贝叶斯安全政策学习框架和机会约束优化程序,以及通过高斯过程和贝叶斯因果森林实现。第 5 节介绍了评估我们建议的数值实验。第 6 节将贝叶斯安全策略学习方法应用于军事安全评估问题。第 7 节总结并讨论了局限性和未来方向。
图 1:20 个子模型分数的汇总。哈姆雷特评估系统 (HES) 使用 20 个子模型分数作为输入,并使用双向和三向决策表对其进行汇总。每个圆圈对应一个基于双向或三向决策表的聚合,不同圆圈使用的决策表相同。
本文提出的方法
现在,我们介绍贝叶斯安全政策学习框架。首先,我们引入了一个新的风险度量--平均条件风险(ACRisk),它表示新政策在协变量条件下产生比基准政策更差的预期效用的概率。然后,我们建议最大化新政策的后验预期值,同时限制后验预期 ACRisk。我们的方法包括两个步骤:首先使用灵活的贝叶斯模型估计条件平均治疗效果(CATE),然后找到最优政策。我们将其表述为一个机会约束优化问题,而这个问题又可以使用基于马尔可夫链蒙特卡罗(MCMC)从 CATE 后验分布中抽取的线性规划来解决。