【AAAI2024教程】物理信息机器学习的最新进展

AAAI 是由国际人工智能促进协会主办的年会，是人工智能领域中历史最悠久、涵盖内容最广泛的国际顶级学术会议之一，也是中国计算机学会（CCF）推荐的 A 类国际学术会议，在人工智能领域享有较高的学术声誉。2024年，AAAI主办地为加拿大温哥华，录用文章2342篇，录用率为23.75%。

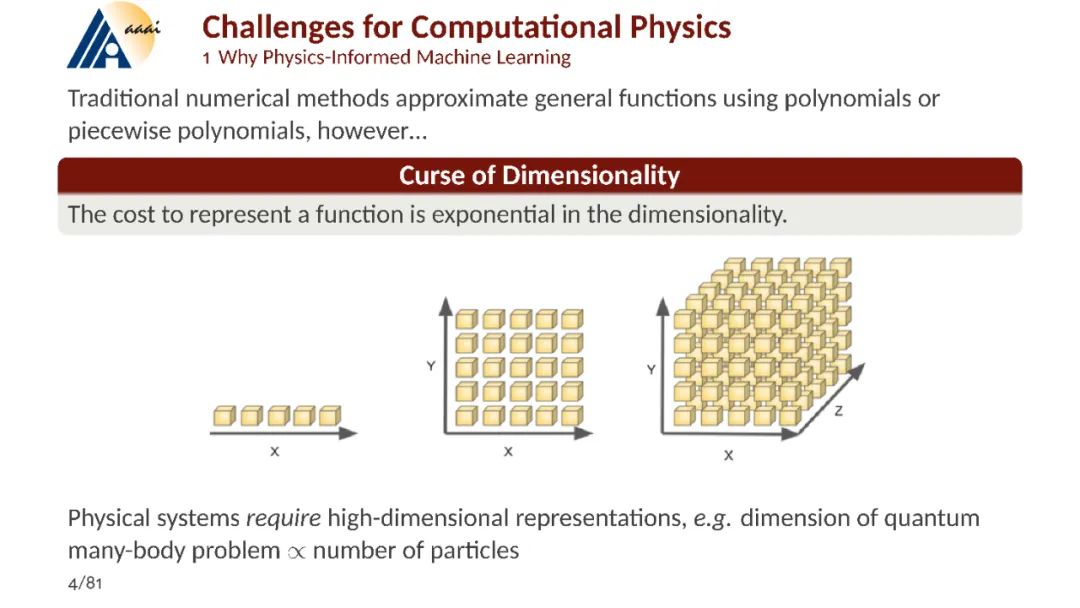
机器学习（ML）正在引领计算科学的一场变革，为复杂的高维函数和泛函构建灵活、通用且高效的近似方法提供了一种新途径。这些新工具的影响开始被理解的一个领域是物理科学，在这个领域中，传统上难以处理的高维偏微分方程现在已经变得可解。本教程将探讨机器学习的发展如何补充物理科学中的计算问题，特别关注解决偏微分方程的问题，其中高维性和数据获取的挑战也随之出现。

本教程将介绍的第一个重要示例是使用深度学习方法解决高维PDEs，这在变分稀有事件计算、多体量子系统和随机控制等方面有广泛应用。本教程还将涵盖研究人员常面临的另一个挑战：在进行不确定性量化时使用的模型复杂性或缺乏规范。因此，另一条研究线旨在使用观测数据恢复底层动态。

本教程将介绍在科学计算中使用机器学习的成熟方法和理论。我们首先讨论如何将物理先验知识整合到机器学习模型中。接下来，我们将讨论这些方法如何帮助解决物理和化学问题。最后，我们将讨论科学机器学习的统计和计算理论。在本教程中，我们不会关注这些理论背后的技术细节，而是讨论它们如何帮助听众理解在微分方程应用中使用机器学习的挑战，并开发解决这些挑战的新方法。

讲者：

参考文献:

[1] Karniadakis G E, Kevrekidis I G, Lu L, et al. Physics-informed machine learning. Nature Reviews Physics, 2021, 3(6): 422-440. [2] Hao Z, Liu S, Zhang Y, et al. Physics-informed machine learning: A survey on problems, methods and applications. arXiv preprint arXiv:2211.08064, 2022. [3] https://2prime.github.io/files/SML/SciMLReport.pdf Physics-informed Neural Network [1] Wang S, Sankaran S, Wang H, et al. An expert’s Guide to Training Physics-informed Neural Networks, arXiv. preprint. [2] Krishnapriyan A, Gholami A, Zhe S, et al. Characterizing possible failure modes in physics-informed neural networks[J]. Advances in Neural Information Processing Systems, 2021, 34: 26548-26560. [3] Lu Y, Chen H, Lu J, et al. Machine learning for elliptic pdes: Fast rate generalization bound, neural scaling law and minimax optimality. ICLR 2022. [4] Marwah T, Lipton Z, Risteski A. Parametric complexity bounds for approximating PDEs with neural networks. Advances in Neural Information Processing Systems, 2021, 34: 15044-15055. Operator Learning: [1] Kovachki N, Li Z, Liu B, et al. Neural operator: Learning maps between function spaces. arXiv preprint arXiv:2108.08481, 2021. [2] Lu L, Jin P, Pang G, et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature machine intelligence, 2021, 3(3): 218-229. [3] Lu L, Meng X, Cai S, et al. A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data. Computer Methods in Applied Mechanics and Engineering, 2022, 393: 114778. [4] Lanthaler S, Mishra S, Karniadakis G E. Error estimates for deeponets: A deep learning framework in infinite dimensions. Transactions of Mathematics and Its Applications, 2022, 6(1). [5] Boullé N, Townsend A. A Mathematical Guide to Operator Learning. arXiv preprint arXiv:2312.14688, 2023.