LSTM长短记,长序依赖可追忆(深度学习入门系列之十四)
摘要:如果你是一名单身狗,不要伤心,或许是因为你的记忆太好了。有时,遗忘是件好事,它让你对琐碎之事不再斤斤计较。然而每当自己记不住单词而“问候亲人”时,也确实气死个人。于是你懂得了如何控制好什么信息该保留,什么信息该遗忘。而长短期记忆网络(LSTM)就是这么干的。来看看是怎么回事吧?
【版权声明】转载请注明出处和作者署名。否则作者和云栖社区有权追究责任。
系列文章
卷地风来忽吹散,积得飘零美如画(深度学习入门系列之十)
局部连接来减参,权值共享肩并肩(深度学习入门系列之十一)
激活引入非线性,池化预防过拟合(深度学习入门系列之十二)
-
循环递归RNN,序列建模套路深(深度学习入门系列之十三)
遗忘是件好事还是坏事?
如果我问你,遗忘,是件好事,还是坏事?
或许你会说,当然是件坏事啊,我可羡慕记忆力好的人了。
可我要告诉你,如果你到现在还记得,两岁时,隔壁家的小女孩“横刀夺爱”,抢了你的棒棒糖,估计你现在还可能单身。如此“记”仇的人,不孤独也难啊?
的确,有时候,遗忘是好事,它会让大脑清理无用“内存”,让你能得以重新起航。其实从脑科学的角度来看,记忆是一种生物运算,它需要消耗能量的。从进化论的角度来看,如果大脑一直长时间运算着用不着的“子程序”,是极不经济的。在物资并不丰裕的远古时代,这样的生物,会被“物竞天择”掉的!因此,遗忘,在某种程度上,是生物的一种自我保护机制。
那遗忘,是件好事咯?或许你会问。
如果是好事,为什么当年背几个英文单词,都要绞尽脑汁,家人还不得不都无辜地“光荣”一大半:Bus(爸死)、Yes(爷死)、Nice(奶死),都Cheese(气死)。
嗯,是的。过犹都不及。我们既需要记忆,也需要遗忘。我们既需要短期记忆(short-term memory),必要时,还要将这些短记忆拉长(long short-term memory),留存下来,以备后用。
聪慧如你,一定猜到了。我要引入本章的主题:长短期记忆(Long Short-Term Memory,简称LSTM)。这个名字有点怪,难道是又长又短的记忆?当然不是,请注意“Short-term”中间有一个短横线“-”连接。这表明,在本质上,LSTM还是短期记忆(short-term memory),只是它历经的时序较长而已。
施密德胡伯是何人?
“LSTM”,名称很拗口啊,为了记忆,我把它记做“老(L)师(S)太(T)忙(M)”。如果于尔根•施密德胡伯(JürgenSchmidhuber)知道我这么玩笑地称呼他的“宝贝”,会不会怼我啊?
施密德胡伯(名字太长,以下简称“胡伯”)又是何许人也?他可来头不小。我们常说深度学习有三大巨头,约书亚•本吉奥(Yoshua Bengio)、扬•勒丘恩(Yann LeCun,又译作“严乐春”)和杰弗里•辛顿(Geoffrey Hinton)。如果把“三大巨头”扩展为“四大天王”的话,这位胡伯应可入围。论开创性贡献,他也算得上深度学习的先驱人物之一。其中他最杰出的贡献,莫过于他于1997年和Hochreiter合作提出的LSTM[1]。因此,胡伯也被尊称为“LSTM之父”。
在前面,之所以我会问胡伯会不会怼我?并不是说他真的会怼一个无名小辈。而是想说,这位老伯本领大,脾气也大啊。有例为证。2015年,前面提及的深度学习三巨头在著名学术期刊《Nature》上发表了一篇《Deep Learning》综述[2],随后胡伯就站出来指责,你们没有充分肯定自己工作的价值。而综述第一作者严乐春亦不甘示弱,随后霸气发文反驳,你丫就值这么多。
有道是,有人的地方,就有江湖。有江湖的地方,就有纷争。
还有一例,值得说道一下。近几年,由伊恩•古德费勒(Ian Goodfellow)等人提出“生成对抗网络”(Generative AdversarialNetworks,GANs),在人工智能领域非常火爆,可称为非监督深度学习的典范之作。这位“好小伙(Goodfellow)”又是谁呢?他就是深度学习三巨头之一的本吉奥(Bengio)的博士生,现就职于谷歌的人工智能团队。严乐春对GAN交口称赞,称其为“20年来机器学习领域最酷的想法”。

图14-1 胡伯与好小伙(Goodfellow)真情互怼
可有人不这么看。2016年12月,在知名的NIPS(Neural Information Processing Systems)大会上,Goodfellow正在做关于GAN的培训宣讲,就发生了尴尬的一幕。不待Goodfellow台上讲完,有位听众就迫不及待,站起来说,自己在1992年提出了一个叫做Predictability Minimization(可预测性最小化,简称 PM)的模型[4],说它如何有效工作,然后话锋一转,问台上的Goodfellow:“你觉不觉得,我的这个PM,跟你的GAN有没有什么类似之处啊?”
来者不善,善者不来。这个来者就是前面提到的胡伯。1987年出生的好小伙Goodfellow初生牛犊不怕虎,当时就有点火大,和胡伯怼上了(感兴趣的读者,可前往视频围观)。为何Goodfellow会恼火?原因很简单,因为胡伯的言外之意就是,你丫的创新并不新鲜,不过是拾我20多年之牙慧罢了。
在这里,我之所以会这么花点笔墨来说胡伯的故事,原因有二:第一他是本章议题LSTM的提出者。二是想介绍一个“二元学习”的方法论。严伯钧老师曾说,如果你没有太多精力,但又想快速建立对一个新领域的感觉,那么最好的办法就是使用“二元学习法”。具体来说,就是找到两位这个领域的代表性人物,最好是针锋相对的代表人物,高手对决,精彩就会纷呈。比如说,在古典音乐领域,听到莫扎特的音乐,就该去找贝多芬的经典欣赏一下;在经济学领域,看到凯恩斯的著作,就该去找哈耶克的书看看。再比如,如果你想了解Goodfellow的GAN,也该找找胡伯的PM模型了解一番。
为什么需要LSTM?
言归正传,让我们回到LSTM的讨论上。近年来,循环神经网络(RNN)在很多自然语言处理项目中取得突破。如果光靠第一代的RNN功力,自然是办不到的。我们知道,传统RNN多采用反向传播时间(BPTT)算法。这种算法的弊端在于,随着时间的流逝,网络层数的增多,会产生梯度消失或梯度爆炸等问题。
“梯度消失”说的是,如果梯度较小的话(<1),多层迭代以后,指数相乘,梯度很快就会下降到对调参几乎就没有影响了。想一想,(0.99)^100是不是趋近于0?
“梯度爆炸”说的是,反过来,如果梯度较大的话(>1),多层迭代以后,又导致了梯度大的不得了。想一想,(1.01)^100是不是也很大?
权重爆炸可能引起权重振荡。梯度消失又导致网络调参失去方向感。这些场景都会让BPTT望“参”兴叹。于是,它在呼唤一个新的策略让RNN复活。
这个策略就是胡伯在1997年提出的(Long Short-Term Memory,LSTM)。由于独特的设计结构,LSTM特别适合于处理时序间隔和延迟非常长的任务,而且性能奇佳。比如说,2009年,用改进版LSTM,赢过ICDAR手写识别比赛冠军。再后来,2014年,Bengio团队提出了一种更加好用的LSTM变体GRU (Gated Recurrent Unit,门控环单元) [6],从而使得RNN的应用,如洪水泛滥,一发不可收拾。2016年,谷歌公司利用LSTM来做语音识别和文字翻译[7]。同年,苹果公司使用LSTM来优化Siri应用[8]。作为非线性模型,LSTM非常适合于构造更大型深度神经网络。
下面,我们就来剖析一下LSTM结构。
拆解LSTM
传统RNN的问题所在
只有定位好问题所在,才能找到机会解决问题。因此,在讲解LSTM原理之间,让我们首先重温一下第一代RNN的问题所在。
让我们考察一下,在原始RNN隐层中的神经元,它只有一个状态,记为h,它对短期输入非常敏感。在第13章中,我们已说明,RNN可利用历史信息(或说上下文信息),把过去的输出,再次循环作为输入,从而可达到更好的预测效果。比如说,“天空中飞来一只__”,这个句子比较短,对于RNN来说,构建的网络层数比较浅,因此我们可以充分利用历史信息,能以较大概率来预测空白区可能是“鸟”或“蜻蜓”之类的飞行动物。
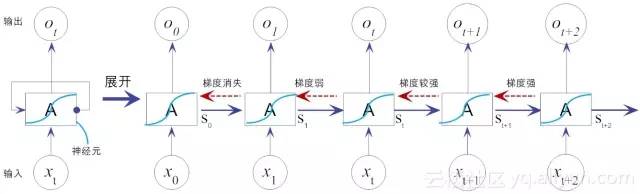
图14-2 上下文较长,无法利用历史信息
但是,如果我们再接着预测如下句子的空白处,句子为“我在中国北京长大,我兄弟5人,我哥叫牛A,我还有三个弟弟分别叫牛C、牛D和牛F,我排名老二,因此大家都叫我牛B,我们都能说一口流利的__”。距离空白处最近的信息提示我们,该处可能要预测一个语言名称。
但世界上的语言上百种,如果我们想缩小语言名称的范围,自然需要利用这个词的上下文信息,但我们很快就会发现,关键词“中国北京”距离“说一口流利的__”这个词汇之间,距离太过遥远。的确,我们也可把RNN的结构做深一点,但限于前文提到的缺点,如梯度弥散等问题,前面网络层的信息如 x0 、x1,..., 等,“流淌”到当前层,有用的信息已所剩无几。或者说,过去的信息已经被抛弃(“遗忘”)了。有时,这样有用但又为抛弃的神经单元,也称为泄漏单元(leaky unit)。
改造的神经元
从上面的分析可知,第一代RNN的问题,出在神经元的功能不健全上,它把该记住的遗忘了,又把该遗忘的记住了。那如何来改造它呢?这个时候,就要体现胡伯提出的LSTM的工作了。LSTM的核心本质在于,通过引入巧妙的可控自循环,以产生让梯度能够得以长时间可持续流动的路径 。
假如我们在原有神经元的基础上再增加一个状态,即c,让它“合理地”保存长期的状态,不就解决问题了吗?其结构如图14-3所示.
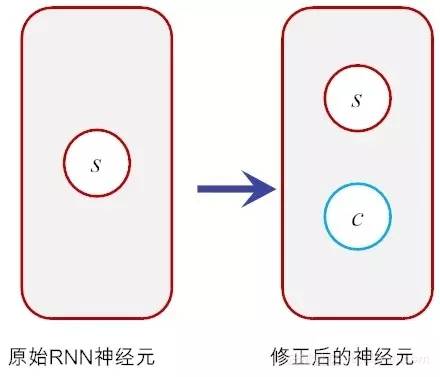
图14-3 调整神经的功能
假设新增加的状态c,称为记忆单元态(cell state),亦称为“记忆块(memory block)”,用以取代传统的隐含神经元节点。它负责把记忆信息从序列的初始位置,传递到序列的末端。下面我们把图14-3按照时间步展开,得到如图14-4所示的示意图。
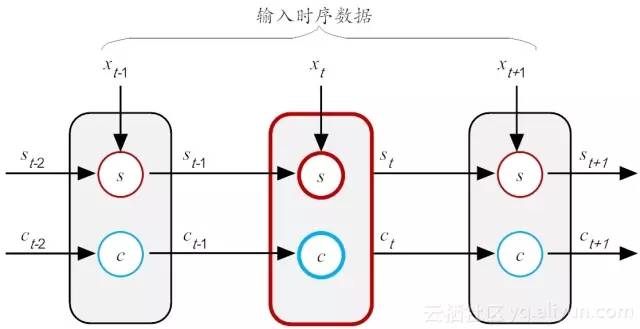
图14-4 按时间步展开的RNN网络
从示意图14-4可看出,在LSTM结构中,在t时刻,当前神经元(粗红线标识)的输入有三个:当前时刻输入值 xt、前一时刻输出值 st−1 和前一时刻的记忆单元状态 ct−1。输出有两个:当前时刻LSTM输出值 st 和当前时刻的记忆单元状态ct。需要注意的是,这里的x,s和c都是向量,里面都包含多个参数值。
现在LSTM关键之处来了,那就是如何有效控制这个长期状态c而为我所用呢?这里,LSTM的设计思路是设计3把控制门开关(gate),从而打造一个可控记忆神经元,如图14-5所示。
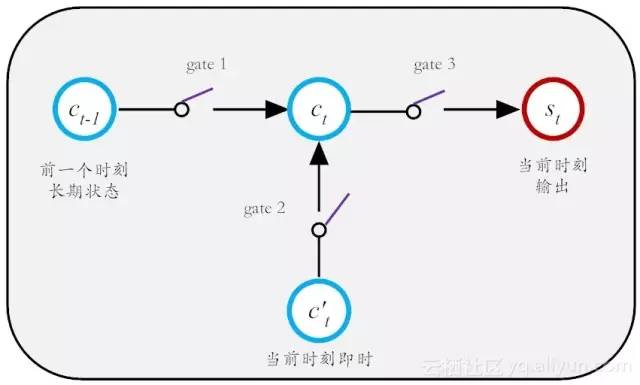
图14-5 长期状态c的控制门的三把开关
这第一把门开关,就是负责决定把前一个长期记忆 ct−1 在多大程度上保留到ct中,它可选择性地遗忘部分之前积累的信息;第二把门开关,就是负责控制以多大程度把当前即时状态存入到长期记忆状态ct中;第三把开关,负责控制是否把长期状态c,作为当前LSTM的输出。有了这三把好用的开关,记忆就如是酒保手中的酒,是“勾兑”可调的。
接下来,让我们要聊聊,在记忆单元中,内部状态c和输出s是如何计算的。
LSTM的前向计算
前文描述的门开关,实际上是一个比喻。在真正的算法中,哪有什么所谓的“开关”?这里的“门开关”,实际上就是一个全连接网络层,它的输入是一个复杂的矩阵向量,而输出是一个0到1之间的实数向量。请注意,由于“门”和“层”的关系是,一个是比喻,一个是实现,所以后文中我们可能混搭表述。
LSTM实际上通过调控某些全连接层网络参数,来达到调控输出的目的。如果输出可控,那么“门”的开和关,就可以模拟出来了。
假设W是门的权重向量,b为偏置向量,这个“门”可表示为公式(14-1)。
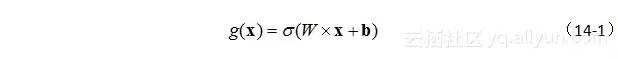
这里,激活函数σ可用挤压函数sigmoid函数的输出来控制门的开与关。由于sigmoid函数的值域被控制在0和1之间。那么,激活函数输出为0时,任何向量与之相乘,结果为0,这就相当于“门”关上了;那如果输出为1时,任何向量与之相乘都不会改变,这就相当于“门”完全开启。当输出值在0至1之间呢,这相当于门是半掩半开的,就可以调控“记忆”的留存程度。
还记得吗?在第13章中,我们说过,人们通常都不具备“马尔科夫链思维”,言外之意,就是说,我们当前的内心感受,都是历史的投射和当下的输入,叠加在一起的结果。这就好比一个场景,“一巴掌挨在脸上(当前输入),新仇旧恨涌上心头(历史记忆)”。
类似地,LSTM也设计两个门控制记忆单元状态c的信息量:一个是遗忘门(forget gate)。所谓的“遗忘”,也就是“记忆的残缺”。它决定了上一时刻的单元状态有多少“记忆”可以保留到当前时刻;另一个是输入门(input gate),它决定了当前时刻的输入有多少保存到单元状态。
在图14-5中,我们说过,LSTM是由三个门来实现的。实际上,为了表述方便,很多文献还添加了一个门,叫候选门(Candidate gate),它控制着以多大比例融合“历史”信息和“当下”刺激。
最后,LSTM还设计了一个输出门(output gate),来来控制单元状态有多少信息输出。下面对这4个门分别进行详细介绍。
遗忘门
如前所述,遗忘门的目的在于,控制从前面的记忆中,丢弃多少信息,或者说要继承过往多大程度的记忆。以音乐个性化推荐为例[9],用户对某位歌手或某个流派的歌曲感兴趣,那么诸如“点赞”、“转发”和“收藏”等这样的正向操作,作为“记忆”,就需要得到加强(换句话说,就需要遗忘得少点)。反之,如果发生了删除、取消点赞或收藏等这类负向操作,对于推荐功能来说,它的信息就应该被“遗忘”得多一些。
遗忘门可通过公式(14-2)所示的激活函数来实现。
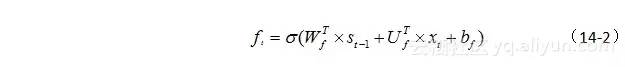
在公式(14-2)中,σ表示激活函数,这里通常为sigmoid。 WTf表示遗忘门权重矩阵, UTf是遗忘门输入层与隐层之间的权重矩阵,bf表示遗忘门的偏置,这里的下标f是“遗忘(forget)”的首字母,为了增强可读性而已,下同。
从公式(14-2)可看出,遗忘门是通过将前一隐层的输出 st−1 与当前的输入xt进行了线性组合,然后利用激活函数,将其输出值压缩到0到1的区间之内。当输出值越靠近1,表明记忆体(cell block)保留的信息就越多。反之,越靠近0,表明保留的就越少。记忆门的工作过程可用图14-6表示。
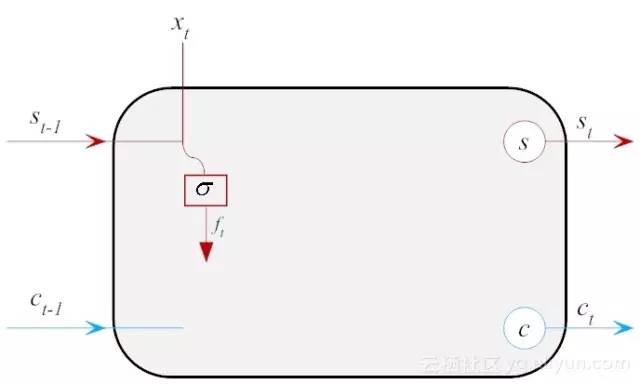
图14-6 遗忘门逻辑设计
输入门的作用在于,它决定了当前时刻的输入信息xt,以多大程度添加至记忆信息流中,它的计算公式几乎和遗忘门完全一致(除了下标和标识不同外),激活函数σ也使用sigmoid,如公式(14-3)所示。
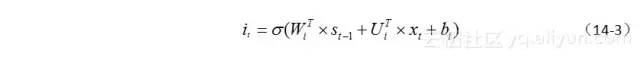
由于和遗忘门功能类似,因此它们的示意图也是类似的,结合遗忘门在一起,如图14-7所示。
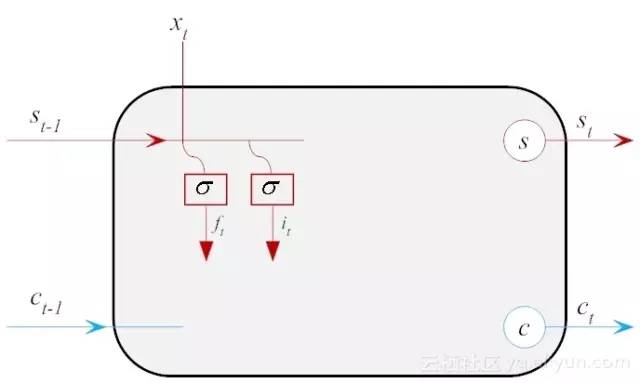
图14-7 输入门逻辑设计
候选门
候选门它可视为一个“勾兑门”,它主要负责“勾兑”当前输入信息和过去记忆信息,也就是候选门负责计算当前输入的单元状态 ,如公式(14-4)所示。
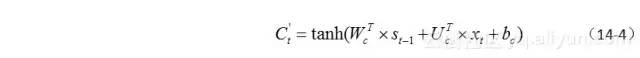
在这里激活函数换成了tanh,它可以把输出值规整到-1和1之间。示意图如图14-8所示。
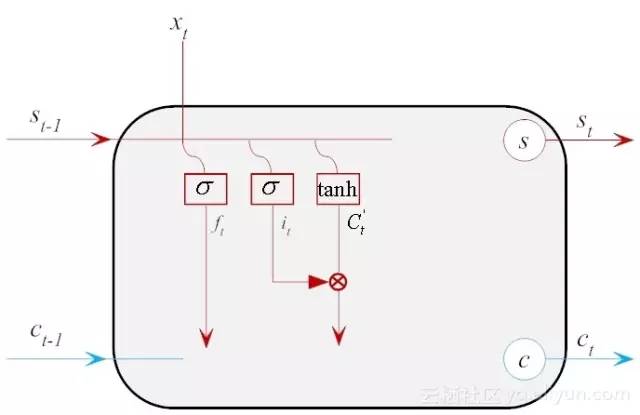
图14-8 计算LSTM的内部的候选门
接下来,我们需要把记忆体中的状态从Ct−1更新到Ct。记忆的更新可由两部分组成:(1) 通过遗忘门过滤掉不想保留得部分记忆,大小可记为:ft×Ct−1;(2)添加当前新增的信息,添加的比例由输入门控制,大小可记为:it×C′t。然后将这两个部分线性组合,得到更新后的记忆信息Ct,如公式(14-5)所示。
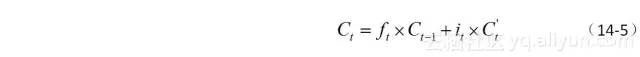
图14-9为输入门与候选门的组合示意图。
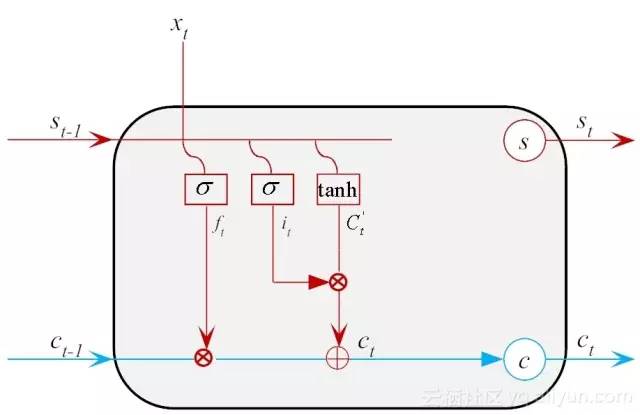
图14-9 输入门与候选门的组合示意图
现在,我们来小结一下遗忘门和输入门的作用。由于遗忘门的存在,它可以控制保存多久之前的信息。由于输入门的存在,它又可以避免当前无关紧要的内容进入到记忆当中。这样一来,该忘记的把它遗忘,该记住的把它记牢,二者相得益彰。
输出门
内部的记忆状态更新完毕之后,下面就要决定是不是输出了。输出门的作用在于,它控制着有多少记忆可以用于下一层网络的更新中。输出门的计算可用公式(14-6)表示。
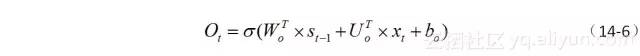
这里激活函数依然是用sigmoid。通过前面的介绍可知,sigmoid会把 Ot规则化为一个0到1之间权重值。
有道是,“话不能说得太满,满了,难以圆通;调不能定得太高,高了,难以合声”。这里的输出,也需要“悠着点”,不能太“任性”的输出,因此还要用激活函数tanh把记忆值变换一下,将其变换为-1至+1之间的数。负值区间表示不但不能输出,还得压制一点,正数区间表示合理的输出。这样有张有弛,方得始终。最终输出门的公式如(14-7)所示。
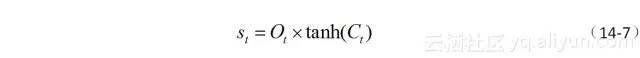
最后,结合前面的门路设计,完整的记忆神经元如图14-10所示。
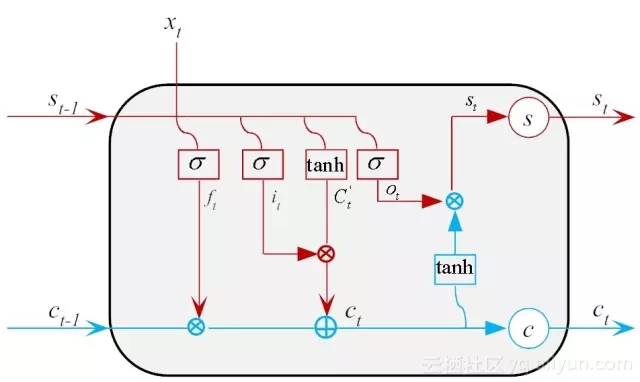
图 14-10 LSTM隐层单元的完整逻辑设计
到此为止,我们剖析了LSTM网络的标准设计流程。但请注意,这并不是唯一的设计方式。事实上,很多文献都会对标准的设计流程有所变更。比如说,Chung等人提出的门控循环单元(Gated Recurrent Unit, GRU)[10]就是其中的佼佼者。GRU在LSTM的基础上进行了简化,它主要做了连个方面的改造:(1)提出了更新门的概念,也就是把输入门和遗忘门合并。(2)把记忆单元Ct和隐层单元st实施了统一。模型的简化,就意味运算上的简化,调参上的便捷。特别是在训练数据很大的情况下,GRU能节省更多时间,从而更能为用户所接受。
LSTM训练
前面我们花了大量的篇幅讨论了LSTM的结构,实际上只是讨论了它的前向传播工作原理,事实上,我们还缺一个LSTM训练算法框架,来调整网络参数。LSTM的参数训练算法,依然是我们熟悉的反向传播算法。对于这类反向传播算法,它们遵循的流程都是类似,简单说来,主要有如下三个步骤:
(1)前向计算每个神经元的输出值。对于LSTM而言,依据前面介绍的流程,按部就班地分别计算出ft,it,ct,ot和st。
(2)确定优化目标函数。在训练早期,输出值和预期值会不一致,于是可计算每个神经元的误差项值,借此构造出损失函数。
(3)根据损失函数的梯度指引,更新网络权值参数。与传统RNN类似,LSTM误差项的反向传播包括两个层面:一个是空间上层面的,将误差项向网络的上一层传播。另一个是时间层面上的,沿时间反向传播,即从当前t时刻开始,计算每个时刻的误差。
然后跳转第(1)步,重新做(1)、(2)和(3)步,直至网络误差小于给定值。
这里,限于篇幅,我们没有给出详细的求导过程,感兴趣的读者,推荐阅读胡伯的开创新性论文[1]和两篇非常优秀的英文博客 [11](国内大部分介绍LSTM的网络文章,都或多或少第借鉴了这篇经典博客)和[12](里面有详细的LSTM的前向和后向传播的详细推导过程)。
小结与思考
现在,我们小结一下本章主要内容。由于传统的RNN存在梯度弥散问题或梯度爆炸问题,导致第一代RNN基本上很难把层数提上去,因此其表征能力也非常有限,应用上性能也有所欠缺。于是,胡伯提出了LSTM,通过改造神经元,添加了遗忘门、输入门和输出门等结构,让梯度能够长时间的在路径上流动,从而有效提升深度RNN的性能。
通过本章的学习,请你思考如下问题:
(1)LSTM是如何避免梯度弥散的?它都使用了那些手段?
(2)根据“无免费午餐原理(No free lunch theorem)”,在任何一个方面的性能提升,都是以牺牲另一个方面性能为代价的,请问LSTM付出的代价(或者说缺点)又是什么?
致谢
由于工作较为繁忙,加之每篇博客都耗时不菲,从构思、查阅资料、撰写和绘图,每一篇文章都得花上好几天。因此,关于深度学习的入门系列,到本章为止,暂时不再更新(或者说第一季结束)。感谢读者朋友这几个月的捧场阅读。
博客能写到14章,首先要感谢云栖社区的支持,特别是阿里云张勇老师的关照(花名:身行;网名:我是主题曲哥哥),感谢他“容忍”我天马行空的写作风格。自然,也得感谢很多论文和网络资源的提供者,没有你们的先行探路,这个系列博客我也是写不出来的。
这个系列博客文章会集结成书,原因是博客文章有如下三个不足,暂时没有办法弥补。
(1)博客内浅尝辄止。为了迎合读者的碎片化阅读习惯,每篇博客都尽可能精简。读者看到每篇博客,基本上都是原文的阉割版。比如说,很多公式就难以给出详细推导过程。
(2)博客范围覆盖不全。虽然更新到第14篇,但深度学习博大精深,很多内容还没有涉及。比如说,Dropout、深度信念网络、生成对抗网络等有价值的内容都没有讲。
(3)博客没有实战环节。目前博客文章仅涉及理论入门,实战环节(如Theano、Caffe及TensorFlow等)一概没有提及。其实,还有第4个原因,有点私心吧。那就是,出书多少能挣点稿费,以补贴我付出的时间和精力。如果读者认可我的工作并手头宽裕的话,希望你到时能赏光买一本。
书名暂定:《品味深度学习》。如果你有更好的题目,不妨给个建议。
出版社:暂时未定(联系邮件:zhangyuhong001@gmail.com)。
出版时间:争取2017年内。
参考文献
[1] Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8):1735.
[2] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553):436-444.
[3] Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]// International Conference on Neural Information Processing Systems. MIT Press, 2014:2672-2680.
[4] Schmidhuber J. Learning Factorial Codes by Predictability Minimization[J]. Neural Computation, 1992, 4(6):863-879.
[5] Liwicki, Fernandez, Bertolami, et al. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition[J]. Physics Letters B, 2008, 450(4):332-338.
[6] Chung J, Gulcehre C, Cho K H, et al. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling[J]. Eprint Arxiv, 2014.
[7] Wu Y, Schuster M, Chen Z, et al. Google's Neural Machine Translation System: Bridging the Gap between Human and Machine Translation[J]. 2016.
[8] Smith, Chris (2016-06-13). "iOS 10: Siri now works in third-party apps, comes with extra AI features". BGR. Retrieved 2017-06-27.
[9] 黄安埠. 深入浅出深度学习.中国工信出版社.2017.6
[10] Chung J, Gulcehre C, Cho K H, et al. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling[J]. Eprint Arxiv, 2014.
[11] Colah. Understanding LSTM Networks,2015
[12] Arun. LSTM Forward and Backward Pass
(更新完毕)
详细内容需点击左下角【阅读原文】进入查看
往期精彩文章
-END-
云栖社区
ID:yunqiinsight
云计算丨互联网架构丨大数据丨机器学习丨运维
点击“阅读原文”阅读该系列文章







