CCCF专栏 | 黄铁军:电脑前传(3):逻辑
事实上,图灵的这个伟大贡献受到了五年之前另一个伟大贡献的启发,这就是本期要介绍的哥德尔不完备定理。
2019年第1期《电脑前传(2):计算》回顾:图灵1936年的论文划定了计算的理论边界:计算是机械地执行长度有限的算法的过程,都可以由图灵机完成;所有算法都可以编码成为一个整数,因此是可数的;尽管如此,并不存在枚举出所有算法的算法。在此基础上,图灵对判定问题给出了否定回答。事实上,图灵的这个伟大贡献受到了五年之前另一个伟大贡献的启发,这就是本期要介绍的哥德尔不完备定理。
古典逻辑
逻辑学的目的是为人类理智建立一个坚实的基础,轴心时代,三大文明分别萌芽出墨辩(古中国)、因明学(古印度)和逻辑学(古希腊)。
我国春秋时期百家争鸣,注重辩论,墨子尤其注重辩论本身的合理性,提出了辩、类、故等逻辑概念,建立了类比、假言、直言、选言、演绎、归纳等一系列的思维方法,建立了中国第一个逻辑体系。因明学以立宗、因、喻三支作法而为言论之法,印度各种宗派常用因明学互相辩论,耆那教、印度教与佛教都继承了这个传统。
古希腊哲人辈出,逻辑学至亚里士多德而确立下来,并作为哲学的一部分,主导西方思想近两千年。如今亚里士多德逻辑被称为词项逻辑,其最基本的概念是项和命题。项是表达某个事物的词类,是命题的基本构件,分为单称项和全称项,两者的区别是亚里士多德“形而上学” 的基础:全称项是亚里士多德逻辑的基本素材,而包含单称项的命题根本就不构成它的一部分。三段论是解释那些真前提的组合产生真结论的形式理论,即一个命题(结论)的必然性从另两个命题(前提)得出的一种推理。命题由主词和谓词两项组成,主词可以是全称(例如“所有人”)或特称(例如“有些人”),谓词可以是“确认”或“否认”,这样就构成了四种命题,亚里士多德用逻辑方阵总结了四种命题之间的联系,但存在缺陷,与现代谓词演算并不兼容。
1656年,戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz, 1646—1716)十岁,他的老师把亚里士多德的逻辑系统介绍给他,唤起了他的数学才能与持续一生的梦想:寻求一个符号系统,每个元素是一个概念,发展一种语言,仅凭符号演算,根据它们之间存在的关系,就可以确定用这种语言写成的句子哪些为真。这里的符号不仅包括算术和代数符号,还包括他所发明的微分和积分,以及化学和天文学使用的符号,每个符号都以一种自然而恰当的方式表示某个确定的概念。莱布尼茨认为,我们需要的是一种普遍文字,即一个不仅真实,而且包含了人类全部思想领域的符号系统。
要实现这个梦想,莱布尼茨认为需要三步[1]:首先创造一套涵盖人类知识全部范围的纲要或百科全书,然后对其背后的观念进行选择,并为每一个观念提供合适的符号,最后是逻辑推演,即采用演绎规则对这些符号进行的操作。莱布尼茨相信纷繁复杂的宇宙可以还原成这样的符号演算,正如他说过的:严肃的具有善良意志的人们围坐在桌子旁解决某个棘手问题,用普遍文字写出这个问题后,人们就可以说:“让我们算一下。”于是人们拿出笔得到一个解答,其对错必然可以为所有人接受。
莱布尼茨在创造普遍文字方面并无具体贡献,但在逻辑代数方面的思想却领先了一个多世纪。就像普通代数规定了数字的操作规则一样,逻辑代数清楚地规定了逻辑概念的操作规则,他一生都沉湎于此,被称为“十七世纪的亚里士多德”。
布尔逻辑
在并不了解莱布尼茨逻辑代数思想的情况下,乔治·布尔(George Boole, 1815—1864)独自一人提出了一种符号逻辑,把逻辑变成了代数。
布尔少而家贫,无钱求学,这位补鞋匠之子自学四门外语,16岁谋得小学教师职务。因收入微薄,买书只选数学书,因为“数学书看的时间可以更长一些”,没机会接触更多类型的论著反倒使他潜心数学,并在此期间产生了布尔代数的基本思想。因为做礼拜时还沉湎于数学,18岁的布尔被其所在的循道宗小学解雇了。
布尔19岁开办了自己的寄宿学校并担任校长,讲了无数的课,但也没耽误阅读当时最重要的数学文献,并在《剑桥数学期刊》发表了不少文章。32岁出版《逻辑的数学分析》,39岁出版《思维的法则》,创立布尔逻辑。42岁当选英国皇家学会院士。布尔的后代名人辈出,代代出院士,人工智能复兴的标志性人物杰弗里·辛顿就是布尔的曾曾外孙。
布尔是怎么想到把逻辑和代数关联到一起呢?布尔回忆说做小学教师时曾灵光乍现[2]。那个时代的人们逐渐认识到代数的力量来自一个事实,即代表着量和运算的符号服从为数不多的几条基本规则或定律。布尔早期曾把代数方法应用于被称为“算子”的对象上,例如把代数方法应用于微分算子,就可以解某些微分方程,这使布尔意识到亚里士多德的逻辑可用代数来表达。
布尔用字母代表一类事物,对应词项逻辑的项。如果x和y分别表示两类事物,那么xy(类似乘法)就表示既属于x又属于y的事物。布尔举例说,如果x代表“白的事物”,y代表“绵羊”,那么xy表示“白绵羊”。布尔马上想到:xx表示什么意思呢?它表示既是白的,又是白的,因此还是……白的,所以xx=x。事实上,布尔整个逻辑体系就建立在这样一个基础上:当x表示一个类时,方程xx=x总为真。
现在到了关键点:回到代数视角,方程xx=x在什么情况下总为真?布尔的回答是:当x=0或1的时候。那么在逻辑体系中,0和1应该表示什么呢?0表示不包含任何事物的类,1表示包含全部事物的类。
乘法有了逻辑对应物,接着看加法和减法。很自然,x+y表示并集,x-y表示在x中但不在y中的事物的集合,1-x表示不在x中的事物的集合。
回到代数视角,xx=x这个方程可以转换成x(1-x)=0,换成逻辑语言就是:没有任何事物既属于给定的类x,同时又不属于类x。这是令布尔最兴奋的一个结果,因为这就是亚里士多德《形而上学》中的矛盾律:
“同一性质既属于又不属于同一个东西,这是不可能的……这是一切原理中最确定无疑的……因此,那些做论证的人把这当成一条最终的意见。因为它依其本性就是其他一切公理的来源。”
x(1-x)=0或xx=x这个代数方程描述的正是作为一切公理之源的基本公理。布尔逻辑就此建立。不难理解布尔为什么把自己的著作题为《作为逻辑和概率的数学理论基础的思维规律研究》[3]。
布尔证明了逻辑演绎可以成为数学的一个分支。正如罗素在《数学原理》中认为的:“纯数学是布尔在一部他称之为《思维规律》的著作中发现的。”逻辑学在徘徊2000多年之后,就此走上了数理逻辑的康庄大道。
逻辑主义
布尔把普通代数作为出发点,用代数符号表示逻辑关系。弗里德里希·弗雷格(Friedrich Frege, 1848—1925)反其道而用之,主张从逻辑学推导出全部数学,开创了逻辑主义。
1879年,弗雷格出版《概念文字——一种模仿算术语言构造的纯思维的形式语言》[4],明确规定了命题符号中的规范形式,明确了所有的演算推理规则,创造了自己的特殊符号来表示逻辑关系,并把这些关系作为逻辑的基础,后来这一思想也为现代逻辑继承[5]。
在这个体系中,命题变元通常使用字母表示,常用逻辑关系如下:
其中,



相对于布尔逻辑,弗雷格最重要的变化是引进了对变元进行限定的量词,最基本的是全称量词∀,另外一个常用量词是存在量词∃。基于这套符号体系,弗雷格提出了把普通数学中的一切演绎推理都包含在内的第一个完备的逻辑体系,后来称为一阶逻辑,因为量词控制的只是变元的个体,而不是变元的集合以及变元之间的关系,否则就是后来的二阶或高阶逻辑了。
弗雷格的符号逻辑体系为所有计算机程序设计语言奠定了基础,但当初弗雷格的雄心是为整个数学奠定可靠基础。19世纪末,数学家们采用公理化方法,已经把几何和微积分建构在实数理论基础上,进而又把实数理论建构在自然数基础上。因此,从逻辑推导出数学的问题,就转换成如何从逻辑推导出自然数系统。
1889年,意大利数学家朱塞佩·皮亚诺(Giuseppe Peano, 1858—1932)提出关于自然数的五条公理,建立起了关于自然数的皮亚诺算术系统(PA)。为了用《概念文字》提出的逻辑发展出自然数系统,弗雷格找到了集合论:基数相同的所有集合组成的集合定义了基数对应的那个自然数。基于这一定义,1893年,弗雷格出版《算术的基本规律》第一卷,阐述了推导出自然数的方法,并继续撰写第二卷,争取为数学奠定可靠的逻辑基础。
1900年国际数学家大会上,法国数学家庞加莱兴高采烈地宣称:“借助集合论的概念,我们可以建造起整个数学大厦……今天,我们可以说,绝对的严格性已经达到了。”数学领袖戴维·希尔伯特(David Hilbert,1862—1943)谨慎乐观,他在会上提出23个问题,2号问题就是算术公理系统的无矛盾性(即一致性):“在这些无数个问题之上,我倾向于确定下面这个问题才是最重要的:这些公理经过有限步骤推演后不会导致相互矛盾的结论……也就是说,我们需要一个关于算术公理一致性的证明。”
很快希尔伯特的担心变为现实。1902年6月,在《算术的基本规律》第二卷付梓之际,弗雷格收到了伯特兰·罗素(BertrandArthur William Russell, 1872—1970)的来信。罗素表示“我在您的著作中找到了在其他逻辑学家的著作中不曾有过的探讨、区分和定义”,但是,“我只在一个地方碰到了困难。”
弗雷格的算术使用了集合的集合,罗素从中发现了悖论。如果一个集合是它自身的一个元素,则称之为异常的,否则是正常的。罗素指出,所有正常集合组成的集合是正常的还是异常的?很容易检查发现,无论哪种选择都自相矛盾。弗雷格马上明白了,他匆忙在第二卷增加了一个补遗:“正当工作就要完成之时,发现那大厦的基础已经动摇。对于一个科学工作者来说,没有什么比这更为不幸的了。伯特兰·罗素的一封信使我置身于这样的境地”。
数学大厦将倾,“捅出娄子”的罗素试图重新奠基,这就是他和怀特海合著的《数学原理》[6],三卷相继于1910年、1912年和1913年出版。这部2000多页的巨著引言只陈述了一个目标,那就是“完整地列出数学推理的所有方法和步骤”,这就是逻辑主义的纲领。
《数学原理》继承了弗雷格的思想和逻辑符号,为了规避悖论,采用了一种精心设计的、使用起来很不方便的分层结构(类型论)。第一步是推出“数”来,过程极其繁琐费力,直到第一卷363页,才成功地用类推演出“1”,第二卷费了很大力气证明了乘法交换律。《数学原理》前三卷覆盖了集合、基数、序数和实数的相关内容,虽然对第四卷几何的基础做了筹划,但整个体系实在太过复杂,十年辛苦不寻常,两位作者再也写不下去了。罗素曾回忆,痛苦在1903和1904年夏天达到高峰,那段日子里,除午饭外,整天就对着白纸枯坐,往往一个字也写不出,这让罗素甚至产生悲观厌世的想法。
图书出版后,罗素迎来了更大的打击,特别是作为前提的可化归性公理遭到了猛烈批评,罗素自己也认为有问题,但是放弃这条公理,很多部分——比如有关实数的部分——就会失去依托。
更大的问题在于这种机械式的罗列背离了数学的根本之美。1958年,王浩在IBM 704 计算机上仅用几分钟时间就证明了《数学原理》的数百条定理。1954年至1963年,赫伯特·西蒙(司马贺)等的启发式程序“逻辑理论家”证明了《数学原理》第二章全部52个定理。他们把这个结果通知罗素,据说罗素回复说:“得知《数学原理》现在可以采用机械方式完成,我很高兴。要是我和怀特海早知道能这么做,就不用浪费10年的时间来手工完成了。”当然,这已经是半个世纪以后的劫后余波了。
希尔伯特纲领
为数学奠定牢固的基础,没有谁比数学界领袖希尔伯特更上心。希尔伯特关于数学基础的思考统称为希尔伯特纲领,经历了20年左右的时间逐步成熟[7],主要体现在1904年海德堡第三届国际数学家大会上的“论逻辑和算术的基础”报告,1917年发表的《公理化思维》,1922年在汉堡的“数学的新基础”讲演和在莱比锡德国自然科学家大会上的《数学的基础》演讲。
希尔伯特提出,为了消除对数学可靠性的怀疑,避免出现悖论,就要设法绝对地证明数学的一致性,使数学奠定在严格的公理化基础上。由此,希尔伯特想到,彻底抛弃公理体系中的含义,构造一个纯粹形式化的公理体系,这个体系内的各种表达式仅仅具有符号意义。如果能证明这种公理体系的一致性,那么把任何含义赋予这个公理体系时,都必然是无矛盾的、一致的。
希尔伯特认为,有三种数学理论[1, 8]:(1) 直观的非形式化的数学理论;(2) 把第一种数学理论形式化,构成形式系统。形式系统包含逻辑演算,直观数学理论中的基本概念转换为形式系统中的初始符号,命题转换为符号公式,推演规则转换为符合公式之间的形式变换,证明转换为符号公式的有穷序列;(3) 描述和研究第二种数学理论的数学,称为元数学或证明论。希尔伯特希望,一致性证明将在元数学内部完成,数学和逻辑则将以一种纯形式的符号语言被发展出来。
布劳威尔(Luitzen Egbertus Jan Brouwer,1881—1966)对希尔伯特纲领嗤之以鼻,希尔伯特的得意门生赫尔曼·外尔也心存疑虑[1]。布劳威尔认为,数学存在于数学家的直觉,最终根源是时间这个“数学的原初直观”,而不是什么形式化表达,为数学寻找一个僵化的形式基础,从根本上就是错误的。外尔认为康托和戴德金等人处理极限的过程“建立在沙滩之上”,对自己重建连续统的努力也不满意,对布劳威尔的直觉主义一见倾心,宣称“布劳威尔……这就是革命。”无论如何,外尔最终还是继承了希尔伯特的衣钵,这是后话。
1928年,希尔伯特和学生阿克曼出版了一册120页的逻辑课本《数理逻辑原理》。这是他1917年冬在哥廷根开设的课程基础上完成的,基本思路是从《数学原理》的逻辑系统开始,先分解成一个个扩展的子集,分别进行单独研究。这本书提出了两个关于弗雷格逻辑(即一阶逻辑)的问题。第一个问题是证明一阶逻辑的完备性,即任何一个从外部看来有效的公式都可以只用课本中提出的规则从系统内部导出。第二个问题就是著名的判定问题。进而,如果一阶逻辑是完备的,希尔伯特还希望证明,把一阶逻辑应用于皮亚诺自然数公理系统算术(PA)也是完备的,即任何一个在PA中表达的命题,或者可以在PA中被证明为真,或者可以在PA中被证明为假。
1930年希尔伯特退休,应邀在柯尼斯堡发表主题为“自然科学与逻辑”的演讲,他再次重申了完备性证明和判定问题证明的梦想,并喊出了“我们必须知道,我们必将知道”的口号。但就在前一天,同样在柯尼斯堡,在一场数学基础研讨会上,24岁的库尔特·哥德尔(Kurt Gödel, 1906—1978)对完备性问题给出了否定回答。6年后,24岁的图灵对判定问题给出了否定回答。
哥德尔定理
1924年,18岁的哥德尔入读维也纳大学,修读理论物理与基础数学。1926年在汉斯·哈恩的引荐下参加维也纳学派的讨论会,研讨会的主题是罗素的《数理哲学导论》,把哥德尔的兴趣从数论拉向了数理逻辑。罗素在《数学原理》阐述的全部数学都可以用一个形式逻辑系统表示,以及罗素的学生维特根斯坦在《逻辑哲学论》中强调的在语言内言说语言的问题,影响了年轻的哥德尔。1928年,希尔伯特和阿克曼的《数理逻辑原理》出版,明确提出一阶逻辑的完备性问题,此时哥德尔正处于博士阶段,就选择这个题目作为其博士论文。1929年哥德尔证明了一阶逻辑的完备性[9],1930年就此获得博士学位。
一阶逻辑(哥德尔论文当时称受限函数演算)的完备性是指该逻辑系统能够表示的任何一个有效的公式,都可以从公理出发通过有限步骤推导出来。一致性则是指所导出的有效公式不相互矛盾。哥德尔在论文开篇就指出他的研究源自罗素和怀特海的《数学原理》以及希尔伯特和阿克曼的《数理逻辑原理》,对一阶逻辑完备性的证明直截了当,所用方法是当时的逻辑学家都很熟悉的。多年之后,哥德尔回顾说这个定理是挪威逻辑学家拉尔夫·司寇仑1922年论文结果“近乎平凡的推论”(不过哥德尔和导师哈恩可能都未读过)。那么为什么希尔伯特的强大团队却苦无对策呢?
主要原因是希尔伯特制定了过于严格的约束。希尔伯特规定,不仅在形式逻辑系统中要采用有限推理(所谓有穷方法),在元数学内也必须采用有限推理,这是他和他的团队证明完备性必须遵循的方针。哥德尔并非希尔伯特嫡系,认为完备性证明是从外部对一个形式逻辑系统进行研究,没必要局限于有穷方法,从而跳出了希尔伯特自设的圈套,顺利解决了这个问题。
1930年9月26日,“精密科学的认识论会议”在柯尼斯堡召开。会议第一天有三个关于数学基础的演讲,各1小时。第一个报告是维也纳学派领军人物鲁道夫·卡尔纳普报告逻辑主义,第二个报告是布劳威尔的学生报告直觉主义,最后是希尔伯特团队骨干冯·诺伊曼报告希尔伯特纲领。第二天除了三个各1小时的报告外,还有三个各20分钟的报告,第一个是哥德尔,介绍了他的博士论文,即弗雷格一阶逻辑的完备性[10]。
会议第三天有一个关于数学基础的圆桌讨论,哥德尔当众宣布了他的不完备性定理,即包含PA的形式系统都是不完备的,冯·诺伊曼立即感觉到这等于宣告了希尔伯特纲领的失败。冯·诺伊曼在希尔伯特团队多年,为解决完备性问题殚精竭虑,会议结束时,冯·诺伊曼找哥德尔进行了一次讨论,决定就此终止自己在逻辑方面的工作,与哥德尔成为了好朋友,称赞哥德尔是亚里士多德以来最伟大的逻辑学家。
1931年哥德尔不完备定理[5, 11]正式发表,要义是:一致的形式系统(只要蕴含皮亚诺公理,即能表达自然数,例如PM系统)必然是不完备的。推论(也称“哥德尔第二不完备定理”):形式系统的一致性不能在系统内推导出来。
哥德尔证明的核心在于构造出在形式系统中不可证实也不可证伪的公式(逻辑命题,在公理体系中称定理)。从内部看,一个形式系统的符号串(公式)本身无意义,因此可以表达多种数学对象(例如自然数系统)。从外部看,一个形式系统不过是按照一定规则排列的符号串,因此可以用自然数进行编码。哥德尔正是抓住了这一点,利用自然数把形式系统内部和外部打通,下面简要描述哥德尔巧妙利用康托对角线法构造这种不可证公式的基本思路。
考察PM中只有一个自然数x作为变量的那些公式R。如果R在PM内是可证的(例如“ x∧x = x”),则记为provable(R),否则记为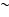
考察对角线上的所有公式Rn(n),从中选出所有不可证的Rn(n),其序号n组成集合K,即K={n|
将公式“n∈K”记为S(n),显然也是R的一员,不妨令它为第q个,即Rq。根据定义,Rq(q)与S(q)、q∈K等价,因此,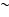
诡异之处在于,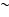
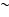
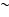
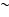
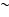
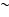
哥德尔构造出了这种必然存在的正反都不可证命题,但并未给出具体实例。直到1982年,才发现第一个在皮亚诺公理体系内不可证的算术命题——Goodstein定理[12]。另一个著名实例是康托的连续统假设,即希尔伯特23个问题中的1号问题,1963年美国数学家保罗·科恩证明连续统假设在集合论下不可证。
走向无穷
命题逻辑是有限的,既是完备的,也是一致的,但连亚里士多德的三段论都分析不了。一阶逻辑也既完备又一致,至今在计算机领域广泛应用,但没能力完整描述和建构包括自然数和实数在内的无穷概念。包含自然数公理系统在内的形式系统表达能力更强,但被哥德尔证明都是不完备的。
哥德尔不完备性定理发表后,罗素曾说:“我以人们寻找宗教信仰的热忱寻找确定性。我以为在数学中最可能找到它。然而,我找到越来越多的不可靠。多年劳累的结论是,我和任何人都不能使数学成为无可怀疑的知识。”不少人就此质疑数学、逻辑甚至科学不可靠,这是极其错误的。
罗素的伤感有他个人因素:耗费了十年光阴,撰写2000余页巨著,试图建立数学大厦,却被哥德尔一篇论文判定永远不可能完工。其实哥德尔并未否定《数学原理》,而是揭示了形式逻辑系统的固有局限性,这种局限性是仅针对该逻辑系统而言的,通过构造逐级增强的等级化的逻辑体系,较弱系统存在的问题可以在更强的系统内解决。《数学原理》并不需要推倒,只是它远不是数学的全部,数学大厦要永远盖下去。
因此,哥德尔定理对罗素来说似乎是坏消息,其实仔细想想,这应该是最大的好消息:至少再也不用为何时收工而心力交瘁了!从弗雷格到罗素再到希尔伯特,都希望为数学奠定一个可靠基础,这种理想无可厚非,但如果他们真的找到一块基石,一劳永逸地建起了数学大厦,数学的使命即告完成,之后再无真正的数学家,至多也只是沿着他们的思想轨道添砖加瓦的数学工匠,数学这颗“人类智慧皇冠上最灿烂的明珠”岂不就此黯然失色?
哥德尔证明完备只在简单逻辑系统中存在,不完备才是复杂逻辑系统的根本特征,打破了试图通过机械推理解决一切数学问题的僵化思维和数千年来人们念念不忘的完备之梦,开启了必须逐层增强逻辑系统才能不断解决问题的正确道路,打开了通向无穷的大门。
希尔伯特也一直希望证明无穷的存在,希望有穷数学能把康托的超限数包括进来,“在我看来,这是数学领地所开出的最令人惊叹的花朵,它是人类纯理性活动的最高成就之一。”在这个意义上,哥德尔定理打破的只是希尔伯特的有穷方法论,而不是他关于无穷的理想。因此,1943年希尔伯特去世后,在他墓碑上镌刻的依然是:
我们必须知道,
我们必将知道。
这正是:
数学山下逻辑村,玉雪为骨冰为魂;
弗雷格植花千树,罗素欲铸磐石根;
布劳威尔凭直觉,希尔伯特立乾坤;
天生一个哥德尔,完备一致成浮云。
作者介绍
|
黄铁军 
•CCF杰出会员。 •北京大学教授,计算机科学技术系主任、数字媒体研究所所长。 •主要研究方向为视觉信息处理和类脑计算。 |

|
脚注
1 形而上学是一个哲学分支学科,是对存在的研究。它亦被认为是对科学以外、无形体、不可证明的事物的研究。马克思主义哲学观认为它是脱离实践的,用“孤立、静止的观点”观察事物的思维方式。
参考文献
[1] 马丁·戴维斯著, 张卜天译. 逻辑的引擎[M]. 湖南科学技术出版社, 2005.
[2] MacHale D. GeorgeBoole: His Life and Work[M]. Dublin: Boole Press, 1985.
[3] Boole G. AnInvestigation of the Laws of Thought, on Which are Founded the MathematicalTheories of Logic and Probabilities[M]. London: Walton & Maberly, 1854.
[4] Frege G.Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinenDenkens[M]. Halle, 1879.
[5] 郝兆宽, 杨睿之, 杨跃. 数理逻辑:证明及其限度[M]. 复旦大学出版社, 2014.
[6] Whitehead A N,Russell B. Principia mathematica 1,2,3 (1 ed.)[M]. Cambridge: CambridgeUniversity Press, 1910,1912,1913.
[7] 张家龙. 论希尔伯特的元数学纲领及其哲学意义[J]. 自然辩证法研究 , 1991(7):22-28.
[8] Heijenoort J V. FromFrege to Gödel[M]. Cambridge, MA: Harvard University Press, 1967.
[9] Gödel K. DieVollständigkeit der Axiome des logischen Funktionenkalküls[J]. Monatshefte für Mathematik und Physik, 1930, 37: 349-360.
[10] Solomon Feferman(ed.). Kurt Gödel Collected Works[M]. Oxford University Press, 1986.
[11] Gödel K. Über formalunentscheidbare Sätze der Principia Mathematica und Verwandter Systeme I[J].Monatshefte für Mathematik und Physik.1931, 38(1): 173–198.
[12] 赵昊彤. “哥德尔不完备定理”到底说了些什么?[OL]. 科学网.http://blog.sciencenet.cn/blog-409681-1067021.html, 2017.
中国计算机学会
长按识别二维码关注我们
CCF推荐
【精品文章】
点击“阅读原文”,前往CCF数图相关栏目。