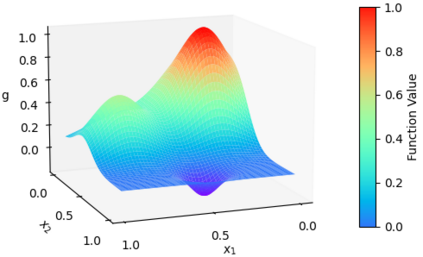
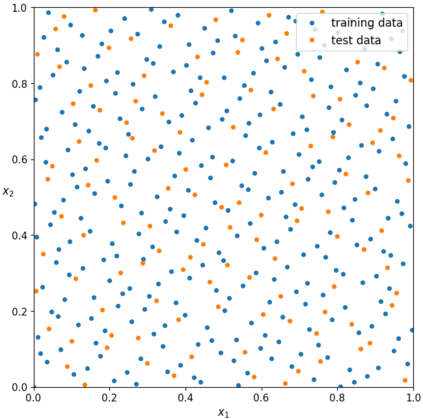
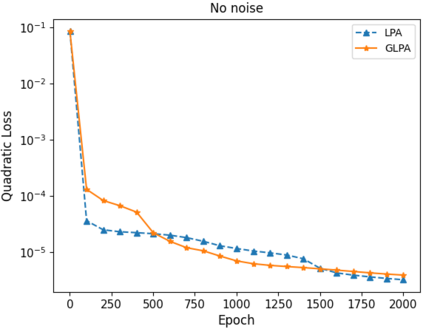
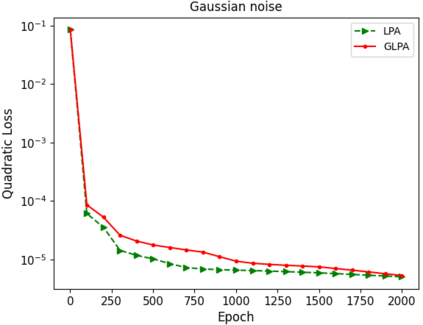
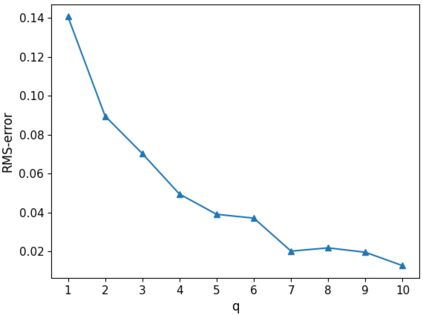
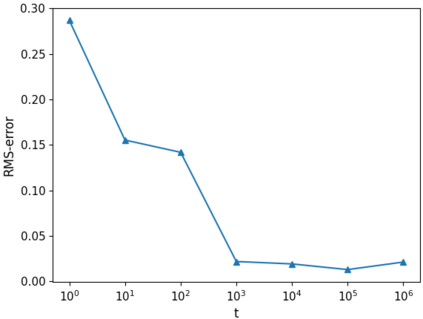
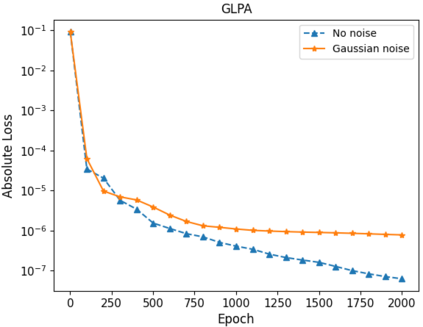
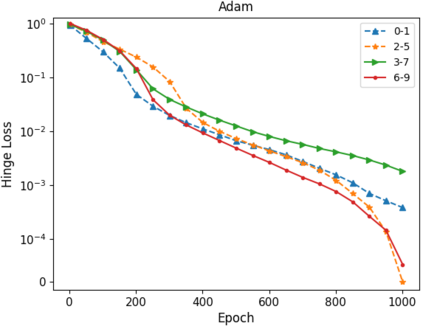
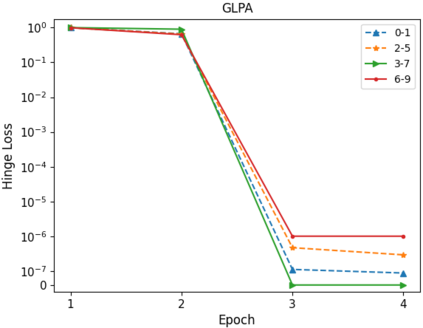
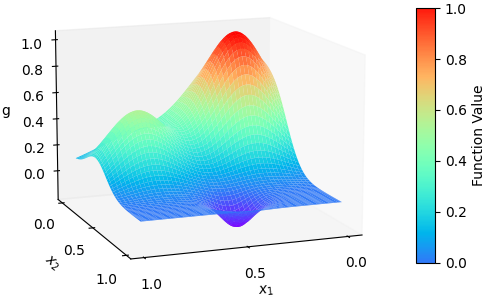
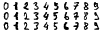In this paper, we use composite optimization algorithms to solve sigmoid networks. We equivalently transfer the sigmoid networks to a convex composite optimization and propose the composite optimization algorithms based on the linearized proximal algorithms and the alternating direction method of multipliers. Under the assumptions of the weak sharp minima and the regularity condition, the algorithm is guaranteed to converge to a globally optimal solution of the objective function even in the case of non-convex and non-smooth problems. Furthermore, the convergence results can be directly related to the amount of training data and provide a general guide for setting the size of sigmoid networks. Numerical experiments on Franke's function fitting and handwritten digit recognition show that the proposed algorithms perform satisfactorily and robustly.
翻译:在本文中,我们使用复合优化算法来解决小类网络问题。我们将小类网络等同地转换为二次组合优化,并提议基于线性准算法和乘数交替方向法的复合优化算法。根据微弱的锐微小算法和规律性条件的假设,算法可以保证与客观功能的全球最佳解决方案趋同,即使在非凝固和非吸附问题的情况下也是如此。此外,趋同结果可以直接与培训数据的数量相关,并为确定小类网络的规模提供一般指南。关于Franke功能安装和手写数字识别的数值实验表明,拟议的算法运作令人满意和稳健。</s>