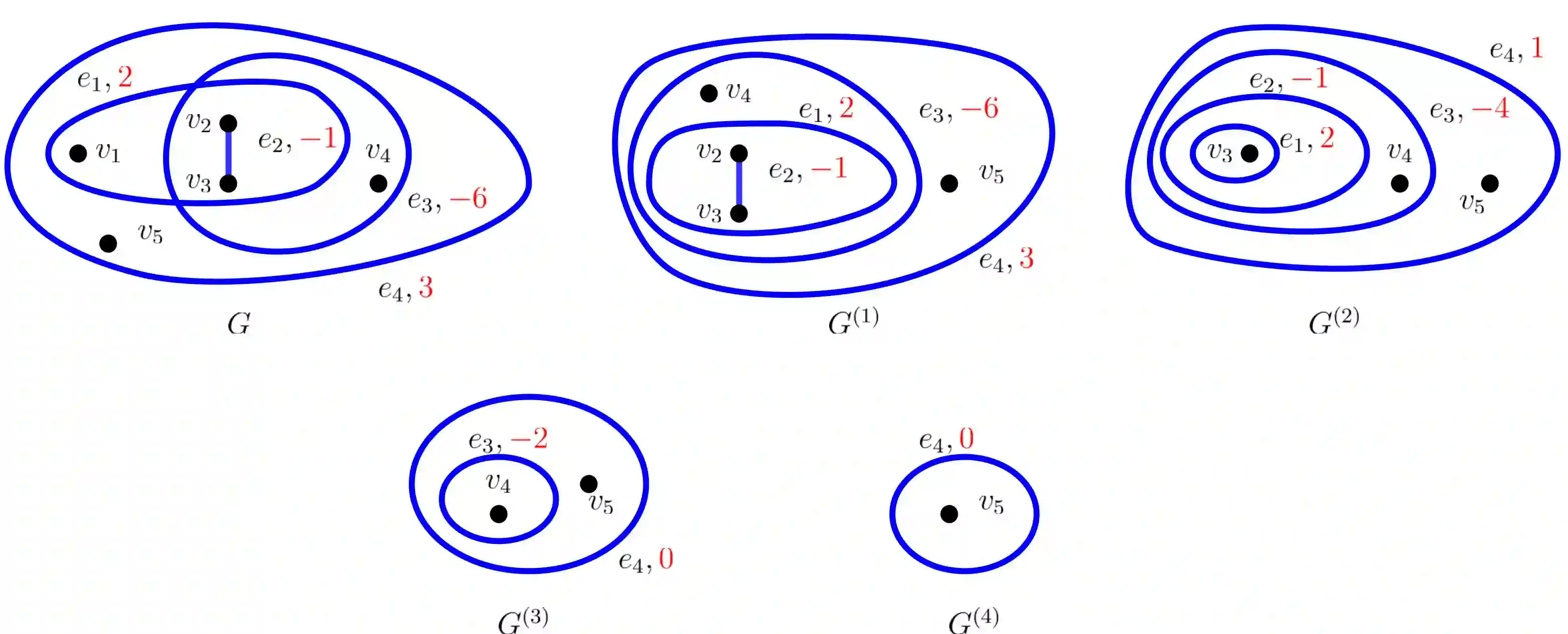
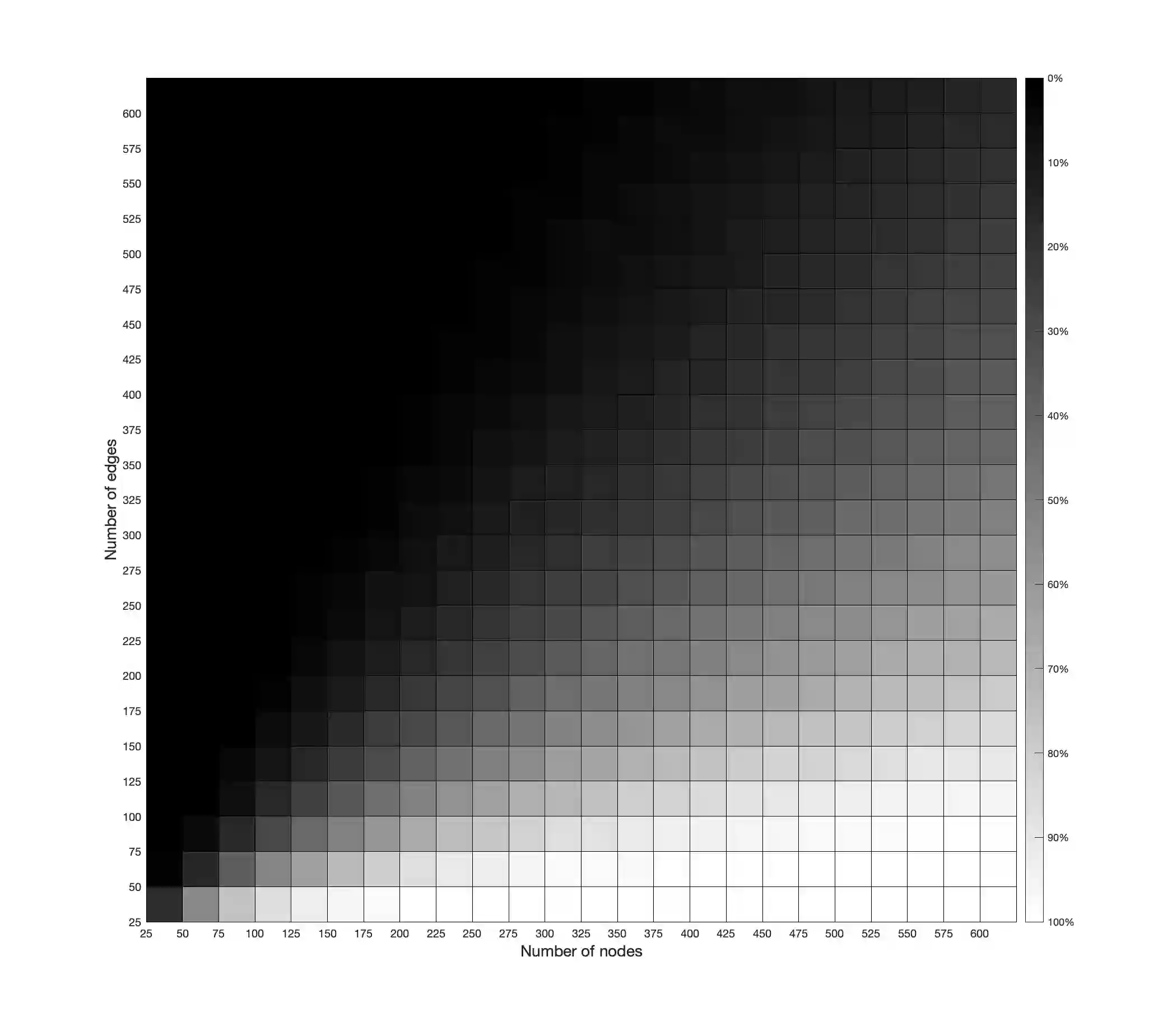
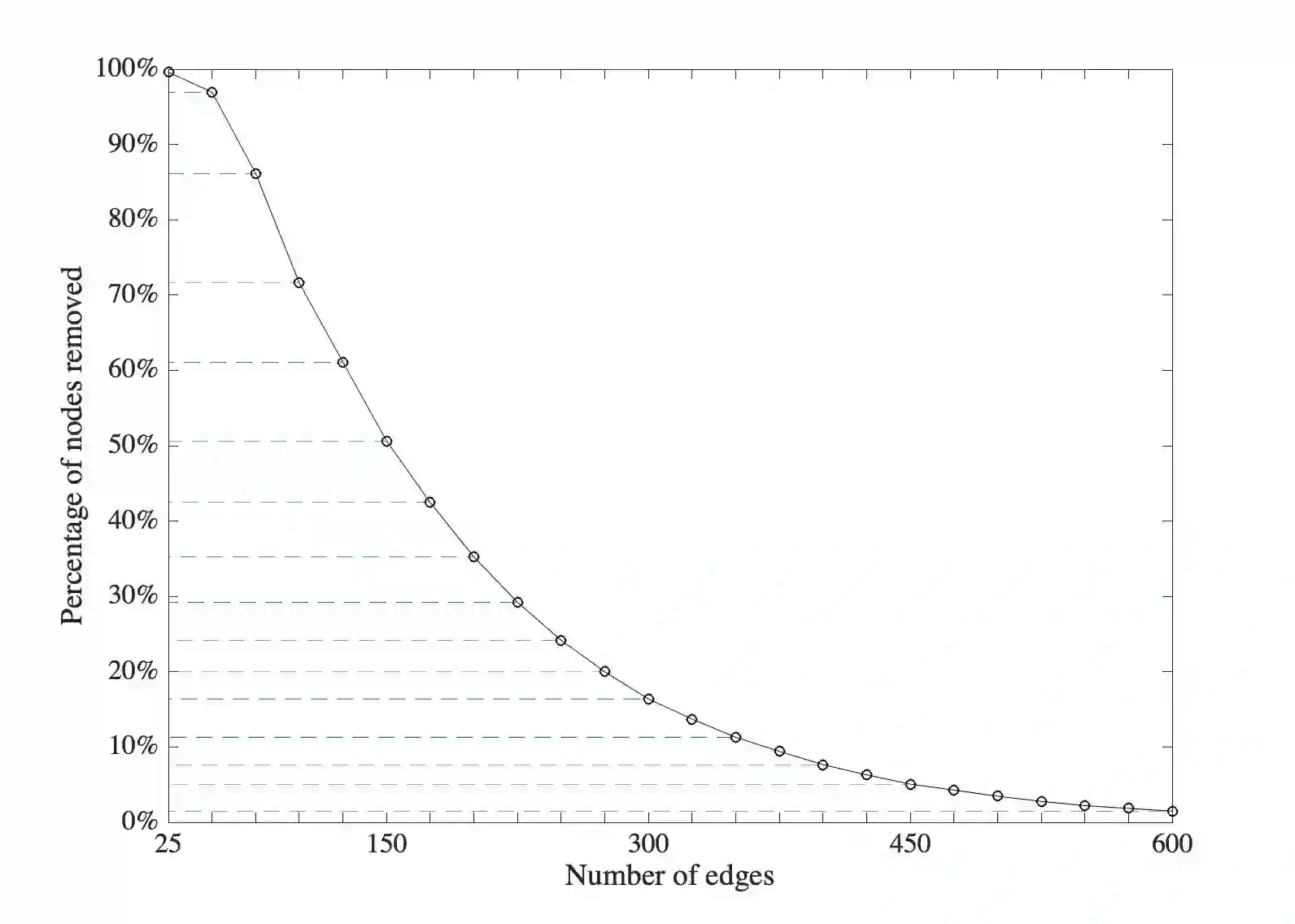
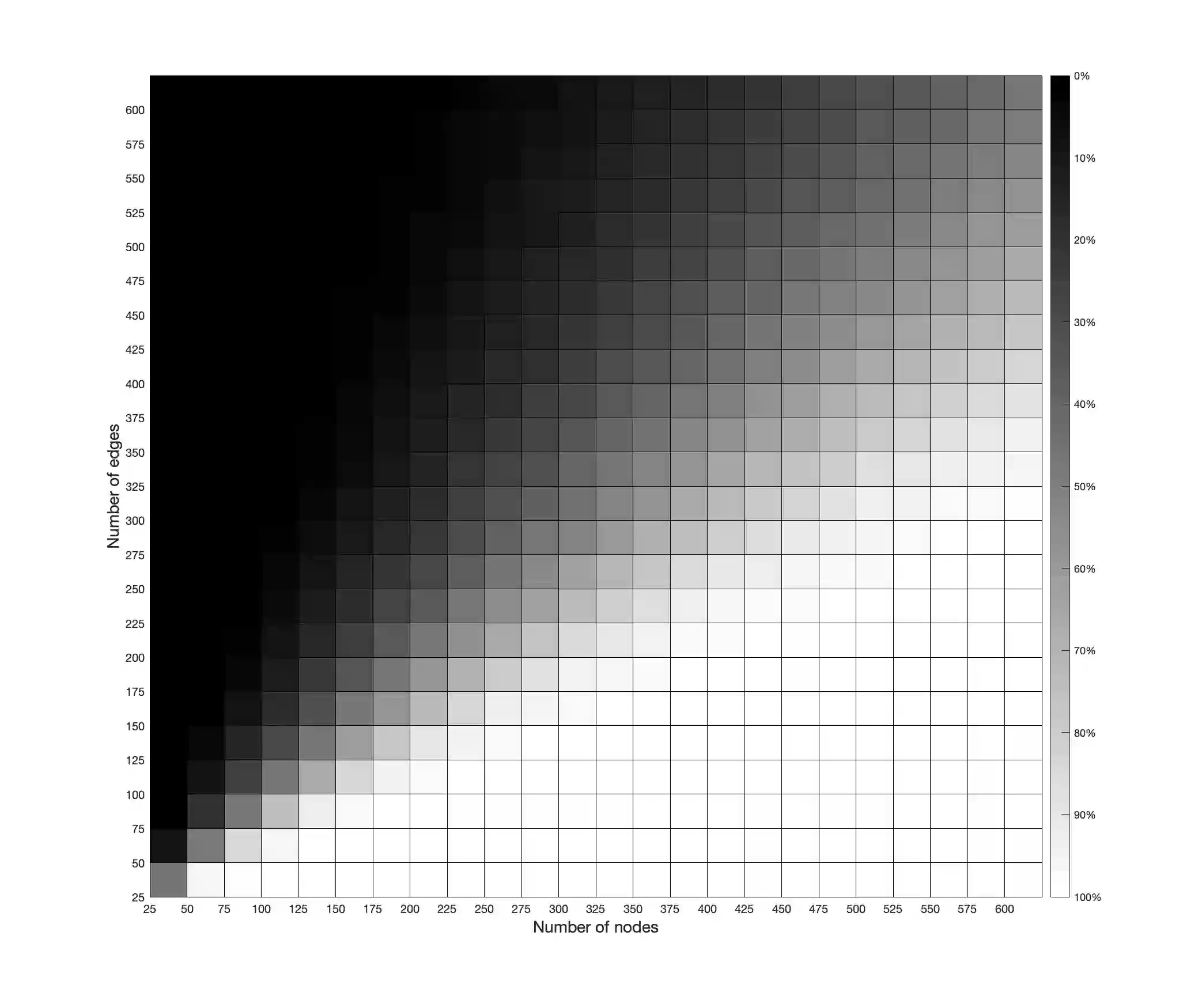
In this work we advance the understanding of the fundamental limits of computation for Binary Polynomial Optimization (BPO), which is the problem of maximizing a given polynomial function over all binary points. In our main result we provide a novel class of BPO that can be solved efficiently both from a theoretical and computational perspective. In fact, we give a strongly polynomial-time algorithm for instances whose corresponding hypergraph is beta-acyclic. We note that the beta-acyclicity assumption is natural in several applications including relational database schemes and the lifted multicut problem on trees. Due to the novelty of our proving technique, we obtain an algorithm which is interesting also from a practical viewpoint. This is because our algorithm is very simple to implement and the running time is a polynomial of very low degree in the number of nodes and edges of the hypergraph. Our result completely settles the computational complexity of BPO over acyclic hypergraphs, since the problem is NP-hard on alpha-acyclic instances. Our algorithm can also be applied to any general BPO problem that contains beta-cycles. For these problems, the algorithm returns a smaller instance together with a rule to extend any optimal solution of the smaller instance to an optimal solution of the original instance.
翻译:在这项工作中,我们增进了对二进制多元优化(BPO)计算基本限值的理解,这是在所有二进制点上最大限度地实现给定多式功能的问题。在我们的主要结果中,我们提供了一种新型的BPO,从理论和计算角度都能有效解决。事实上,我们给相应的高光度高光度高光度高光度的事例提供了强烈的多元时间算法。我们注意到,在包括关系数据库计划和树上的多重切割问题在内的若干应用中,乙周期性假设是自然的。由于我们检验技术的新颖性,我们获得了一种也从实际角度引人注意的算法。这是因为我们的算法非常简单,运行时间是高光度节点和边缘非常低的多元数。我们的结果完全解决了BPO相对于环度高光度高光度高光度的计算复杂性,因为问题在阿尔法周期上是硬化的。由于我们的验证技术的新颖性,我们也可以从一个实用角度获得一种有趣的算法。这是因为我们的算法非常简单,我们的算法可以用来执行,而运行时间是用来把最佳的比标准法返回任何比最优的自动的方法。