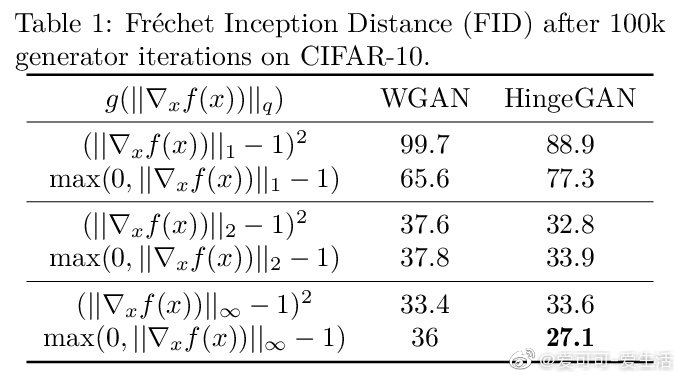
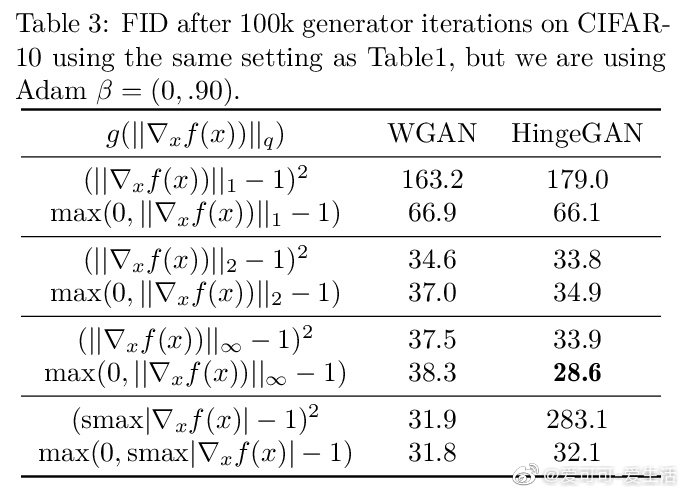
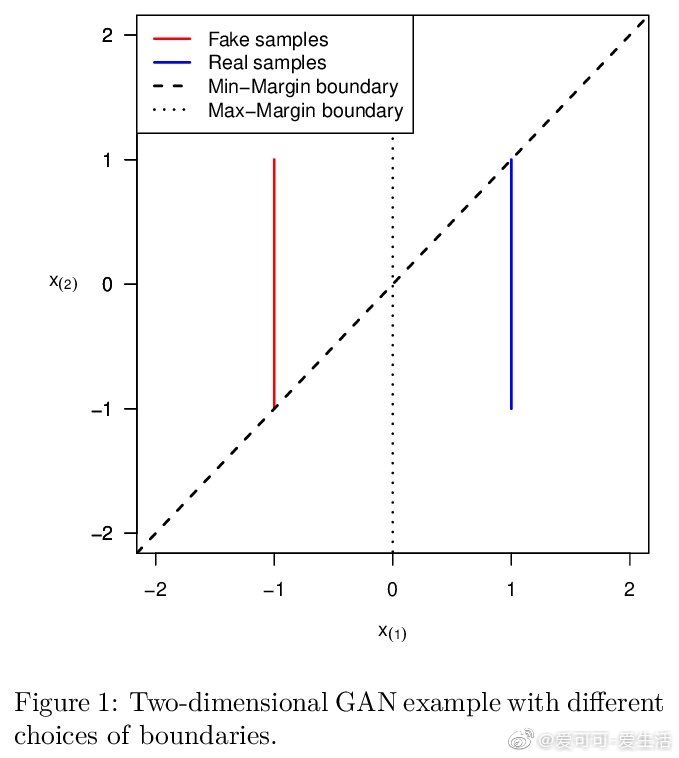
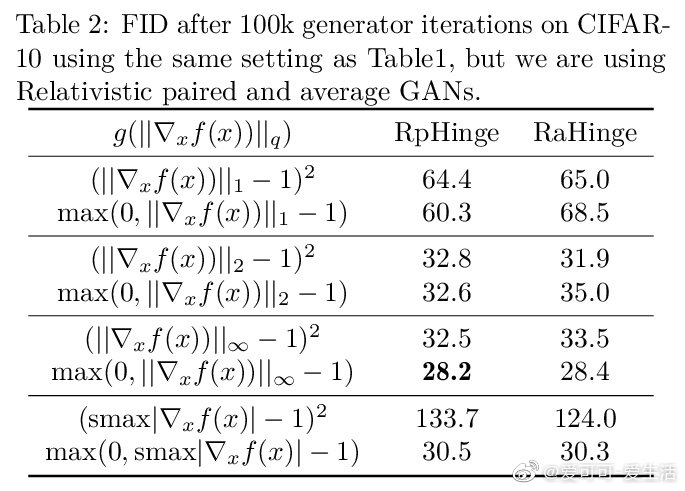
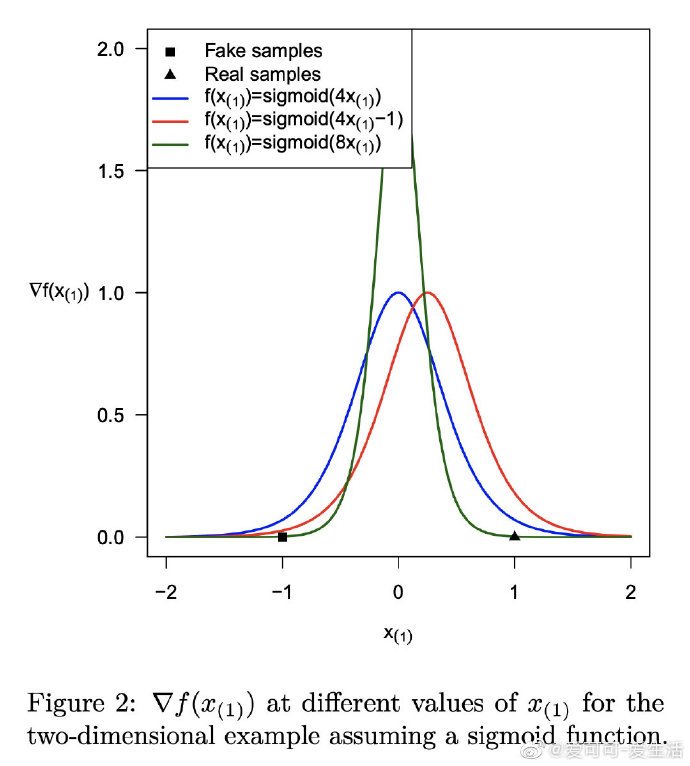
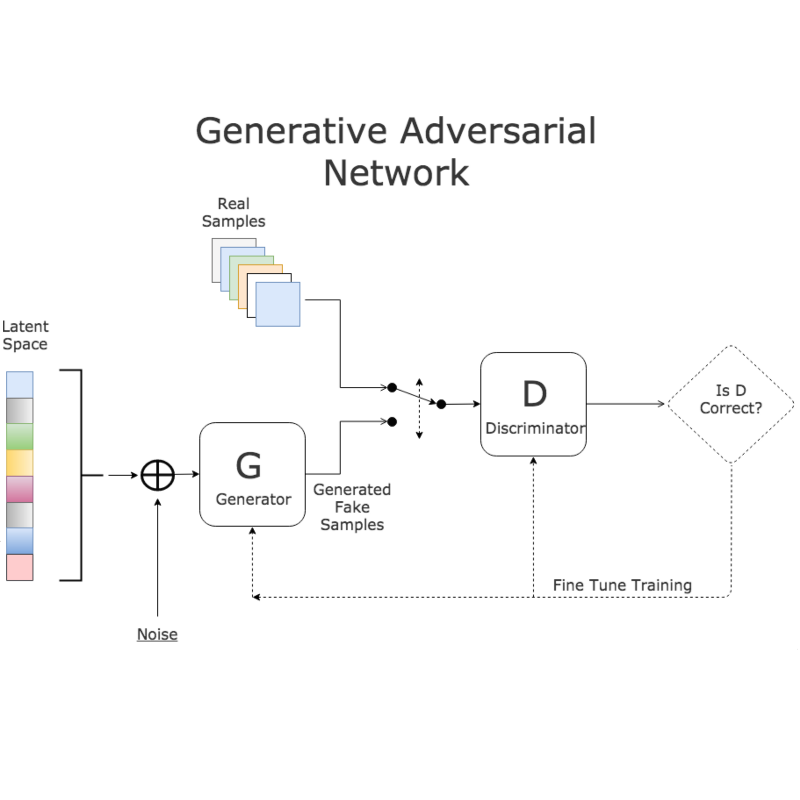
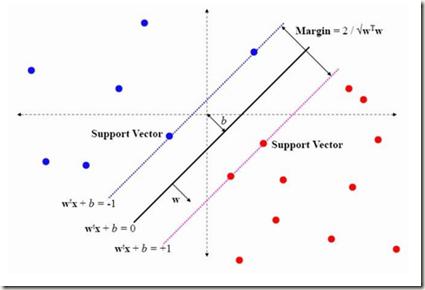
*《Connections between Support Vector Machines, Wasserstein distance and gradient-penalty GANs》A Jolicoeur-Martineau, I Mitliagkas [Mila] (2019)
成为VIP会员查看完整内容
相关内容
We propose a scalable Gromov-Wasserstein learning (S-GWL) method and establish a novel and theoretically-supported paradigm for large-scale graph analysis. The proposed method is based on the fact that Gromov-Wasserstein discrepancy is a pseudometric on graphs. Given two graphs, the optimal transport associated with their Gromov-Wasserstein discrepancy provides the correspondence between their nodes and achieves graph matching. When one of the graphs has isolated but self-connected nodes ($i.e.$, a disconnected graph), the optimal transport indicates the clustering structure of the other graph and achieves graph partitioning. Using this concept, we extend our method to multi-graph partitioning and matching by learning a Gromov-Wasserstein barycenter graph for multiple observed graphs; the barycenter graph plays the role of the disconnected graph, and since it is learned, so is the clustering. Our method combines a recursive $K$-partition mechanism with a regularized proximal gradient algorithm, whose time complexity is $\mathcal{O}(K(E+V)\log_K V)$ for graphs with $V$ nodes and $E$ edges. To our knowledge, our method is the first attempt to make Gromov-Wasserstein discrepancy applicable to large-scale graph analysis and unify graph partitioning and matching into the same framework. It outperforms state-of-the-art graph partitioning and matching methods, achieving a trade-off between accuracy and efficiency.
This paper focuses on the discrimination capacity of aggregation functions: these are the permutation invariant functions used by graph neural networks to combine the features of nodes. Realizing that the most powerful aggregation functions suffer from a dimensionality curse, we consider a restricted setting. In particular, we show that the standard sum and a novel histogram-based function have the capacity to discriminate between any fixed number of inputs chosen by an adversary. Based on our insights, we design a graph neural network aiming, not to maximize discrimination capacity, but to learn discriminative graph representations that generalize well. Our empirical evaluation provides evidence that our choices can yield benefits to the problem of structural graph classification.
Over the past decade, knowledge graphs became popular for capturing structured domain knowledge. Relational learning models enable the prediction of missing links inside knowledge graphs. More specifically, latent distance approaches model the relationships among entities via a distance between latent representations. Translating embedding models (e.g., TransE) are among the most popular latent distance approaches which use one distance function to learn multiple relation patterns. However, they are not capable of capturing symmetric relations. They also force relations with reflexive patterns to become symmetric and transitive. In order to improve distance based embedding, we propose multi-distance embeddings (MDE). Our solution is based on the idea that by learning independent embedding vectors for each entity and relation one can aggregate contrasting distance functions. Benefiting from MDE, we also develop supplementary distances resolving the above-mentioned limitations of TransE. We further propose an extended loss function for distance based embeddings and show that MDE and TransE are fully expressive using this loss function. Furthermore, we obtain a bound on the size of their embeddings for full expressivity. Our empirical results show that MDE significantly improves the translating embeddings and outperforms several state-of-the-art embedding models on benchmark datasets.
In this paper we study the convergence of generative adversarial networks (GANs) from the perspective of the informativeness of the gradient of the optimal discriminative function. We show that GANs without restriction on the discriminative function space commonly suffer from the problem that the gradient produced by the discriminator is uninformative to guide the generator. By contrast, Wasserstein GAN (WGAN), where the discriminative function is restricted to $1$-Lipschitz, does not suffer from such a gradient uninformativeness problem. We further show in the paper that the model with a compact dual form of Wasserstein distance, where the Lipschitz condition is relaxed, also suffers from this issue. This implies the importance of Lipschitz condition and motivates us to study the general formulation of GANs with Lipschitz constraint, which leads to a new family of GANs that we call Lipschitz GANs (LGANs). We show that LGANs guarantee the existence and uniqueness of the optimal discriminative function as well as the existence of a unique Nash equilibrium. We prove that LGANs are generally capable of eliminating the gradient uninformativeness problem. According to our empirical analysis, LGANs are more stable and generate consistently higher quality samples compared with WGAN.
We know SGAN may have a risk of gradient vanishing. A significant improvement is WGAN, with the help of 1-Lipschitz constraint on discriminator to prevent from gradient vanishing. Is there any GAN having no gradient vanishing and no 1-Lipschitz constraint on discriminator? We do find one, called GAN-QP. To construct a new framework of Generative Adversarial Network (GAN) usually includes three steps: 1. choose a probability divergence; 2. convert it into a dual form; 3. play a min-max game. In this articles, we demonstrate that the first step is not necessary. We can analyse the property of divergence and even construct new divergence in dual space directly. As a reward, we obtain a simpler alternative of WGAN: GAN-QP. We demonstrate that GAN-QP have a better performance than WGAN in theory and practice.
While Generative Adversarial Networks (GANs) have empirically produced impressive results on learning complex real-world distributions, recent work has shown that they suffer from lack of diversity or mode collapse. The theoretical work of Arora et al.~\cite{AroraGeLiMaZh17} suggests a dilemma about GANs' statistical properties: powerful discriminators cause overfitting, whereas weak discriminators cannot detect mode collapse. In contrast, we show in this paper that GANs can in principle learn distributions in Wasserstein distance (or KL-divergence in many cases) with polynomial sample complexity, if the discriminator class has strong distinguishing power against the particular generator class (instead of against all possible generators). For various generator classes such as mixture of Gaussians, exponential families, and invertible neural networks generators, we design corresponding discriminators (which are often neural nets of specific architectures) such that the Integral Probability Metric (IPM) induced by the discriminators can provably approximate the Wasserstein distance and/or KL-divergence. This implies that if the training is successful, then the learned distribution is close to the true distribution in Wasserstein distance or KL divergence, and thus cannot drop modes. Our preliminary experiments show that on synthetic datasets the test IPM is well correlated with KL divergence, indicating that the lack of diversity may be caused by the sub-optimality in optimization instead of statistical inefficiency.
The potential of graph convolutional neural networks for the task of zero-shot learning has been demonstrated recently. These models are highly sample efficient as related concepts in the graph structure share statistical strength allowing generalization to new classes when faced with a lack of data. However, knowledge from distant nodes can get diluted when propagating through intermediate nodes, because current approaches to zero-shot learning use graph propagation schemes that perform Laplacian smoothing at each layer. We show that extensive smoothing does not help the task of regressing classifier weights in zero-shot learning. In order to still incorporate information from distant nodes and utilize the graph structure, we propose an Attentive Dense Graph Propagation Module (ADGPM). ADGPM allows us to exploit the hierarchical graph structure of the knowledge graph through additional connections. These connections are added based on a node's relationship to its ancestors and descendants and an attention scheme is further used to weigh their contribution depending on the distance to the node. Finally, we illustrate that finetuning of the feature representation after training the ADGPM leads to considerable improvements. Our method achieves competitive results, outperforming previous zero-shot learning approaches.
We propose the Wasserstein Auto-Encoder (WAE)---a new algorithm for building a generative model of the data distribution. WAE minimizes a penalized form of the Wasserstein distance between the model distribution and the target distribution, which leads to a different regularizer than the one used by the Variational Auto-Encoder (VAE). This regularizer encourages the encoded training distribution to match the prior. We compare our algorithm with several other techniques and show that it is a generalization of adversarial auto-encoders (AAE). Our experiments show that WAE shares many of the properties of VAEs (stable training, encoder-decoder architecture, nice latent manifold structure) while generating samples of better quality, as measured by the FID score.
Methods that align distributions by minimizing an adversarial distance between them have recently achieved impressive results. However, these approaches are difficult to optimize with gradient descent and they often do not converge well without careful hyperparameter tuning and proper initialization. We investigate whether turning the adversarial min-max problem into an optimization problem by replacing the maximization part with its dual improves the quality of the resulting alignment and explore its connections to Maximum Mean Discrepancy. Our empirical results suggest that using the dual formulation for the restricted family of linear discriminators results in a more stable convergence to a desirable solution when compared with the performance of a primal min-max GAN-like objective and an MMD objective under the same restrictions. We test our hypothesis on the problem of aligning two synthetic point clouds on a plane and on a real-image domain adaptation problem on digits. In both cases, the dual formulation yields an iterative procedure that gives more stable and monotonic improvement over time.
Partially inspired by successful applications of variational recurrent neural networks, we propose a novel variational recurrent neural machine translation (VRNMT) model in this paper. Different from the variational NMT, VRNMT introduces a series of latent random variables to model the translation procedure of a sentence in a generative way, instead of a single latent variable. Specifically, the latent random variables are included into the hidden states of the NMT decoder with elements from the variational autoencoder. In this way, these variables are recurrently generated, which enables them to further capture strong and complex dependencies among the output translations at different timesteps. In order to deal with the challenges in performing efficient posterior inference and large-scale training during the incorporation of latent variables, we build a neural posterior approximator, and equip it with a reparameterization technique to estimate the variational lower bound. Experiments on Chinese-English and English-German translation tasks demonstrate that the proposed model achieves significant improvements over both the conventional and variational NMT models.
相关VIP内容
专知会员服务
31+阅读 · 2020年3月5日
专知会员服务
20+阅读 · 2019年10月30日
相关资讯
相关论文
Hongteng Xu,Dixin Luo,Lawrence Carin
3+阅读 · 2019年10月9日
Younjoo Seo,Andreas Loukas,Nathanaël Perraudin
4+阅读 · 2019年6月5日
Afshin Sadeghi,Damien Graux,Jens Lehmann
4+阅读 · 2019年5月29日
Zhiming Zhou,Jiadong Liang,Yuxuan Song,Lantao Yu,Hongwei Wang,Weinan Zhang,Yong Yu,Zhihua Zhang
7+阅读 · 2019年2月15日
Jianlin Su
4+阅读 · 2018年12月15日
Yu Bai,Tengyu Ma,Andrej Risteski
4+阅读 · 2018年6月27日
Michael Kampffmeyer,Yinbo Chen,Xiaodan Liang,Hao Wang,Yujia Zhang,Eric P. Xing
13+阅读 · 2018年5月31日
Ilya Tolstikhin,Olivier Bousquet,Sylvain Gelly,Bernhard Schoelkopf
6+阅读 · 2018年3月12日
Ben Usman,Kate Saenko,Brian Kulis
3+阅读 · 2018年1月30日
Jinsong Su,Shan Wu,Deyi Xiong,Yaojie Lu,Xianpei Han,Biao Zhang
5+阅读 · 2018年1月16日