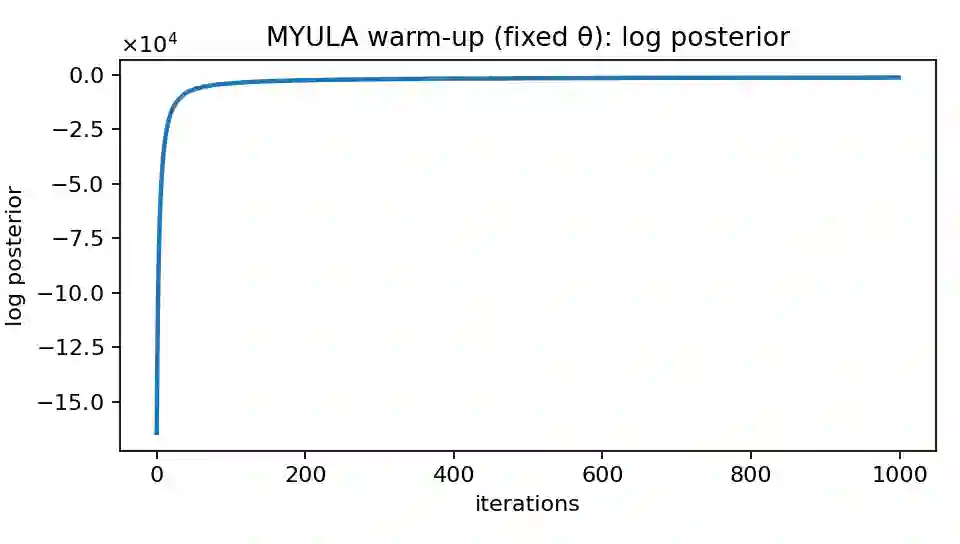
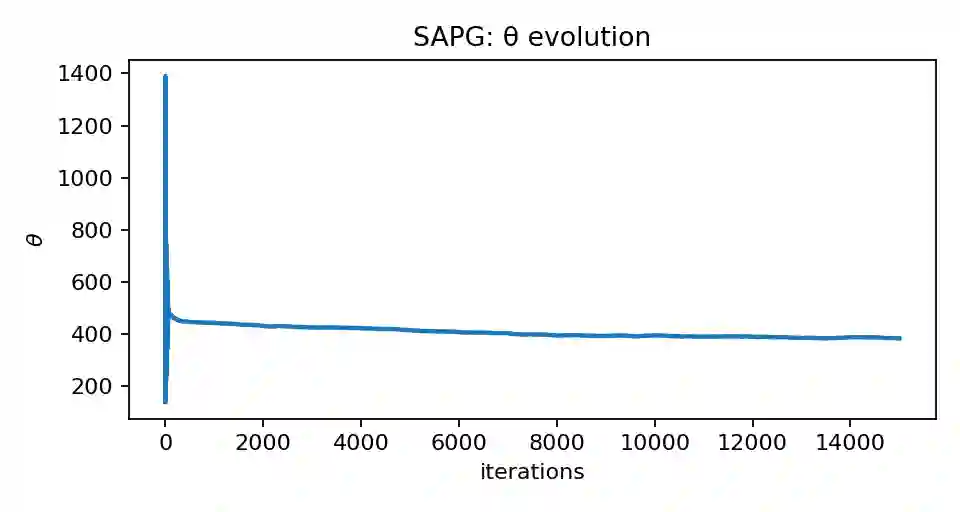
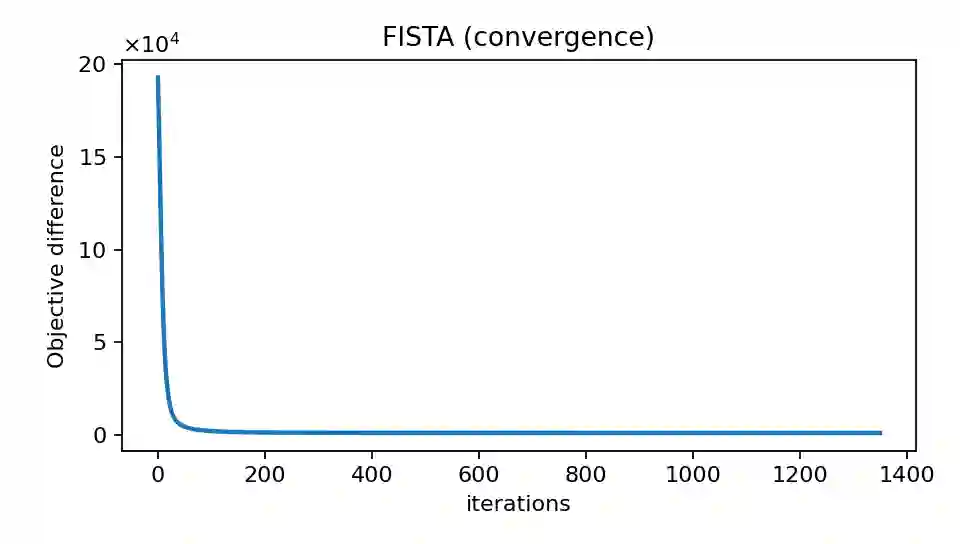
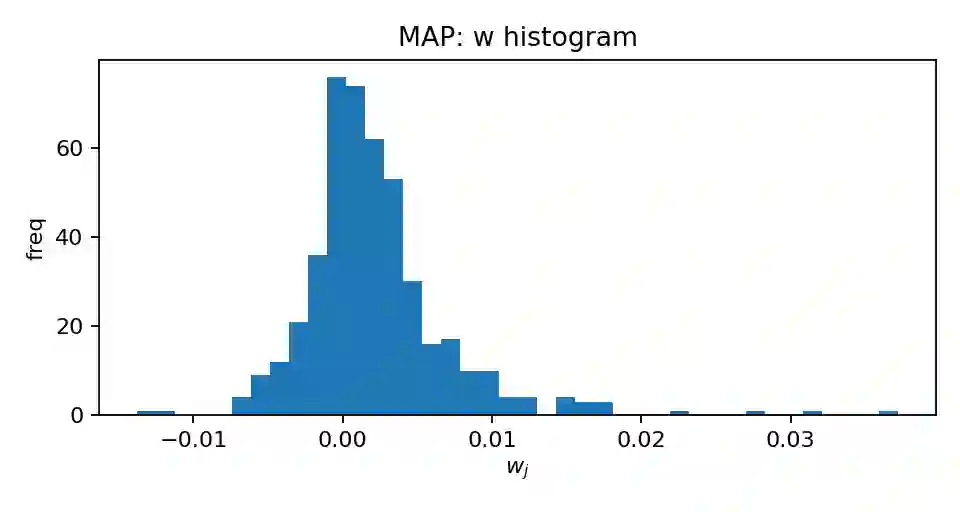
We study the construction and rebalancing of sparse index-tracking portfolios from an operational research perspective, with explicit emphasis on uncertainty quantification and implementability. The decision variables are portfolio weights constrained to sum to one; the aims are to track a reference index closely while controlling the number of names and the turnover induced by rebalancing. We cast index tracking as a high-dimensional linear regression of index returns on constituent returns, and employ a sparsity-inducing Laplace prior on the weights. A single global shrinkage parameter controls the trade-off between tracking error and sparsity, and is calibrated by an empirical-Bayes stochastic approximation scheme. Conditional on this calibration, we approximate the posterior distribution of the portfolio weights using proximal Langevin-type Markov chain Monte Carlo algorithms tailored to the budget constraint. This yields posterior uncertainty on tracking error, portfolio composition and prospective rebalancing moves. Building on these posterior samples, we propose rules for rebalancing that gate trades through magnitude-based thresholds and posterior activation probabilities, thereby trading off expected tracking error against turnover and portfolio size. A case study on tracking the S&P~500 index is carried out to showcase how our tools shape the decision process from portfolio construction to rebalancing.
翻译:本研究从运筹学视角探讨稀疏指数跟踪投资组合的构建与再平衡问题,重点关注不确定性量化与可实施性。决策变量为总和约束为1的投资组合权重;目标是在控制持仓数量与再平衡所致换手率的同时紧密跟踪基准指数。我们将指数跟踪问题建模为指数收益对成分股收益的高维线性回归,并对权重施加诱导稀疏性的拉普拉斯先验。通过单一全局收缩参数权衡跟踪误差与稀疏性,并采用经验贝叶斯随机逼近方案进行校准。在此校准条件下,我们采用针对预算约束设计的近端朗之万型马尔可夫链蒙特卡洛算法近似投资组合权重的后验分布,从而获得跟踪误差、投资组合构成及预期再平衡操作的后验不确定性。基于这些后验样本,我们提出通过幅度阈值与后验激活概率控制交易的再平衡规则,从而在预期跟踪误差与换手率、投资组合规模之间进行权衡。通过对标普500指数的案例研究,展示我们的工具如何塑造从投资组合构建到再平衡的决策过程。