第一集团军司令部(第一集团军)负责规划与管理预备役部队的动员行动,该部队由美国陆军预备役(USAR)与陆军国民警卫队(ARNG)组成。这些预备役部队的战备状态较低且资源配备不如陆军现役部队。陆军预备役与陆军国民警卫队依赖动员部队生成基地(MFGI)进行快速训练并为全球部署做准备。第一集团军采用基于启发式的流程来分配单位并安排动员部队生成基地的训练计划。当前流程可能需要数周时间生成解决方案,可能提供不可行的解决方案,且难以扩展至大规模行动。本研究开发了一种整数线性规划模型,用于在大规模动员行动中将单位分配至动员部队生成基地。使用开源与商业求解器评估模型在仿真数据上的性能。经证明,该模型能在更短时间内针对更大规模问题生成最优解决方案。本研究为第一集团军提供了灵活的动员规划工具。
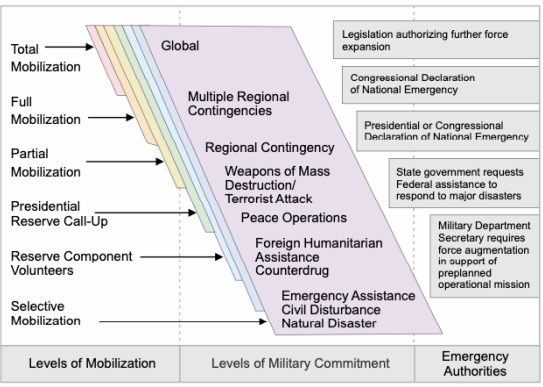
图2.1。按军事承诺的动员水平。军事承诺的增加要求更高的当局批准更大规模的动员。
第一集团军司令部(第一集团军)负责规划与管理陆军预备役及陆军国民警卫队的动员行动。第一集团军必须确定单位在动员规划期间进行训练的时间与地点。他们当前使用由少数参谋军官执行的基于启发式的流程。该流程可能需要数周时间制定解决方案,缺乏分配决策透明性,且在参谋人员更替时存在流程性能下降的风险。这些局限在稳态可预测的动员行动中尚可管理,但在大规模动员行动中将无法应对。第一集团军需要更好的方法来确定单位动员的时间与地点。
本研究开发了一种优化模型,用于确定陆军预备役与陆军国民警卫队单位的动员时间与地点。该模型是一种具有基于惩罚的目标函数的整数线性规划。单位被赋予在动员期间完成训练的指定日期。训练计划若在任何其他日期完成训练或训练持续时间过长将受到惩罚。目标函数还使用单位特定权重,使用户能够针对同一问题实例探索具有不同质量的解决方案。通过简单问题对比,展示了模型相对于朴素方法的性能。使用免费与商业求解器比较模型在人工数据集上的性能。采用免费求解器时,该模型可解决代表第一集团军最常见动员类型的问题。商业求解器使模型能够解决在六个月内对多达100个单位与10个军事基地具有严格训练要求的实例。
该优化模型提升了第一集团军规划动员行动的能力。模型可在一天而非数周内生成解决方案。许多先前难以处理的问题可直接求解。即使问题实例规模过大,模型仍可在数分钟内生成可行解。模型可生成支持军事决策过程的多种解决方案。该模型正与第一集团军在“陆军优势”平台上的现有流程集成。本研究可改进第一集团军的稳态动员行动,降低实施大规模动员行动的门槛,并为陆军提供战略工具。
本研究分为五个章节:引言、背景、方法论、分析与结论。第二章为背景部分。背景部分通过概述联合动员流程来界定问题,讨论大规模动员行动与常规动员的差异,概述第一集团军采用的当前流程,并整合相关研究。第三章为方法论部分。方法论章节阐述了影响设计选择的限制与假设,借助简单问题讨论模型,并介绍人工数据集。第四章为分析部分。分析章节阐述了问题规模对模型的影响,讨论了实施完全热启动的流程,分析了模型性能,并评估了使用商业求解器的价值。第五章为结论部分。结论部分总结了研究成果及其应用,为第一集团军提供建议,并指出未来工作的机遇。