《反潜战中的效能评估研究》最新77页报告

本论文研究了搜索潜艇使用对数螺旋搜索模式重新定位近期丢失目标潜艇的能力。研究通过开发随机时间步进仿真模型进行数据采集与定量分析，核心效能指标包括重获接触时间、重获接触时的距离以及总体探测概率。自变量涵盖目标潜艇的假定航速、搜索潜艇的初始距离以及目标机动频率。研究发现：该搜索模式在前两小时内效能最优，此后定位目标的可能性显著下降；目标机动频率与探测概率呈正相关，搜索潜艇初始距离与探测概率呈负相关；若搜索潜艇基于目标可能航速的极端值（如最低或最高航速）规划机动策略，其性能将显著降低。本研究通过定量分析验证了对数螺旋搜索模式的有效性，并为未来反潜战术开发提供了框架支撑。

背景与战略意义
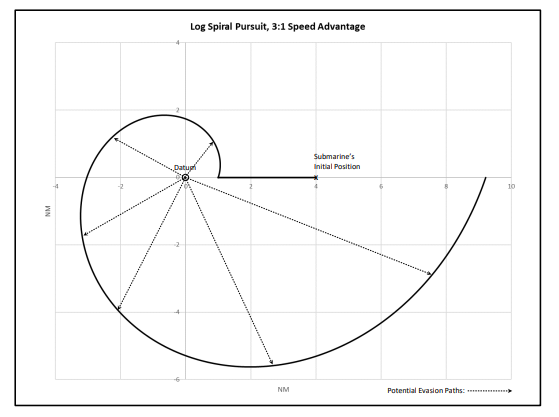
在大国竞争时代，美国及其近等对手正通过军事、经济、政治与外交手段争夺全球影响力（Savoy与Staguhn，2022年）。就军事手段而言，制海权的核心要素之一是潜艇。鉴于潜艇的多功能性与隐蔽性，全球各国持续投入大量资源发展潜艇技术。为应对对手的技术飞跃，美国持续研发技术与战术以维持水下优势。自二战以来，潜艇已采用平行搜索、蛇行搜索、方形搜索、扇形搜索及屏障巡逻等多种模式定位敌方潜艇（Champagne等，2003年）。然而，理论上还存在基于严密数学推导的搜索模式，例如对数螺旋搜索模式（见图1，搜索潜艇与目标潜艇的相对速度比为3:1）（Nahin，2007年，第85-90页）。

理论假设与仿真模型
该搜索模式在数学上被证明能够确保目标定位，但其有效性依赖四项假设：1）搜索潜艇保持声学优势；2）目标潜艇无法探测搜索潜艇（Cares，2024年）；3）搜索潜艇对目标具有显著速度优势（Cares，2024年）；4）目标潜艇保持恒定的规避航向与航速（Cares，2024年）。本研究通过仿真模拟挑战上述假设：构建包含蓝方（搜索潜艇）与红方（目标潜艇）的随机时间步进仿真模型。红方潜艇采用二维随机游走模型，其航向在每次机动时从0至2π弧度的均匀分布中随机抽取，航速从6至14节的均匀整数分布中随机选择。红方机动间隔时间服从泊松过程，每次间隔为随机指数变量。蓝方潜艇在每次场景中起始于红方初始位置的正南方，初始距离可变。蓝方机动分为两阶段：第一阶段朝红方最后已知位置抵近至1海里内；第二阶段启动螺旋搜索。

探测概率建模与效能指标
蓝方潜艇在每个时间步的探测概率由分段函数定义，最大探测距离为4海里。若红方潜艇航向与蓝方航向夹角在±30度范围内（正对或背对），探测概率将乘以0.1的衰减系数，以模拟此类方位下潜艇声学辐射能量的衰减效应。本仿真的效能指标（MOE）包括重获接触时间、重获接触距离以及红方潜艇的总体探测概率。这些指标对评估对数螺旋机动的效能与安全性至关重要：重获接触时间越短，目标完全丢失的可能性越低；重获接触距离影响潜艇安全性与反探测风险；总体探测概率直接反映战术有效性。通过对初始分离距离、红方假定航速及红方机动频率等变量的分析，研究得出以下结论：