【ICML2025】免费的Fisher？通过回收平方梯度累加器近似Fisher信息矩阵

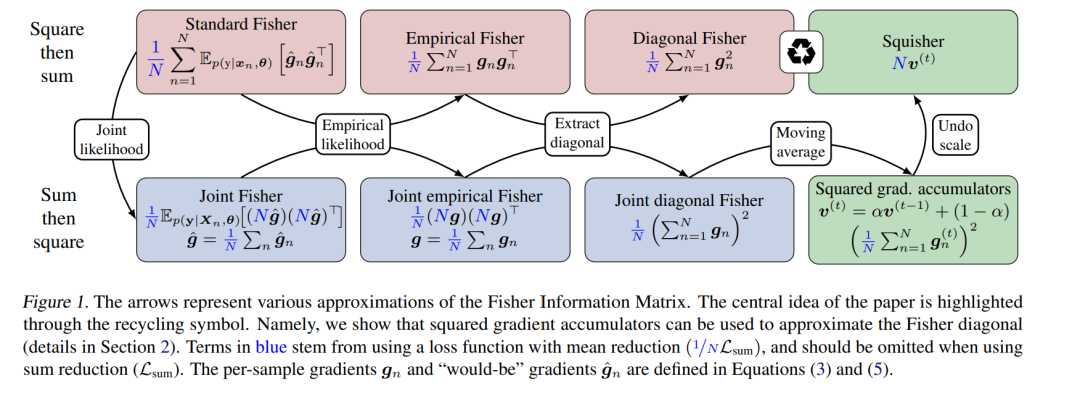
模型的Fisher信息矩阵的对角线部分（即“Fisher对角线”）常被用作衡量参数敏感性的一种方式。 通常，Fisher对角线是通过对模型似然函数关于其参数的梯度平方进行采样估计，并在几百到几千个样本上取平均而得到的——这一过程会带来不小的计算开销。与此同时，诸如广泛使用的Adam优化器这类自适应梯度方法，在训练过程中会计算梯度平方的滑动平均。 因此，本文探索了一个问题：是否可以通过“回收”在训练过程中已计算好的平方梯度累加器，从而“免费”获得Fisher对角线的近似值。 通过覆盖Fisher对角线五种应用场景的一系列综合实验证明，这种方法（我们称之为“Squisher”，即以平方梯度累加器近似Fisher）在表现上与Fisher对角线一致，并优于其他基线方法。 此外，我们还阐明了Squisher与Fisher对角线之间的具体差异，并对它们各自的影响进行了实证量化。