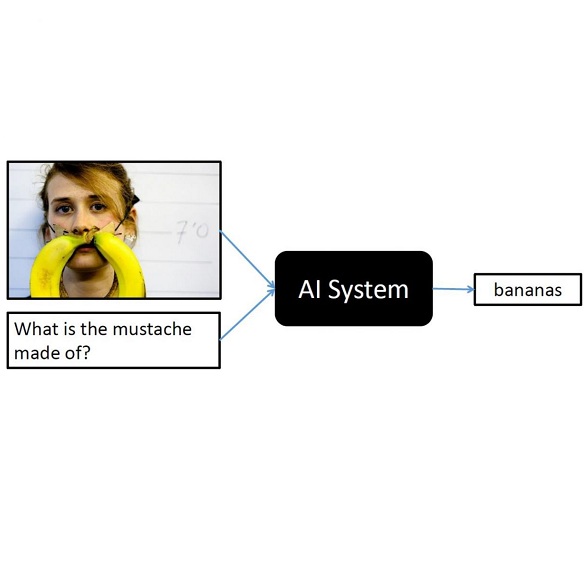
Accurately answering a question about a given image requires combining observations with general knowledge. While this is effortless for humans, reasoning with general knowledge remains an algorithmic challenge. To advance research in this direction a novel `fact-based' visual question answering (FVQA) task has been introduced recently along with a large set of curated facts which link two entities, i.e., two possible answers, via a relation. Given a question-image pair, deep network techniques have been employed to successively reduce the large set of facts until one of the two entities of the final remaining fact is predicted as the answer. We observe that a successive process which considers one fact at a time to form a local decision is sub-optimal. Instead, we develop an entity graph and use a graph convolutional network to `reason' about the correct answer by jointly considering all entities. We show on the challenging FVQA dataset that this leads to an improvement in accuracy of around 7% compared to the state of the art.
翻译:准确回答关于特定图像的问题需要结合观察和一般知识。 虽然对于人类来说,这是毫无努力的,但一般知识的推理仍然是一个算法挑战。为了推进这方面的研究,最近提出了一个新的“基于事实”的视觉问题回答(FVQA)任务,同时提出了大量经过分析的事实,将两个实体联系起来,即通过关系,两个可能的答案。鉴于一个问题-图像对,深网络技术被用来连续减少大量事实,直到最后最后两个实体中的一个被预测为答案。我们观察到,一个在时间考虑一个事实以形成当地决定的连续过程是次最佳的。相反,我们开发了一个实体图,并使用一个图形革命网络,通过共同考虑所有实体来“推理”正确答案。我们用具有挑战性的FVQA数据集显示,这导致比艺术状态的准确率提高约7%。