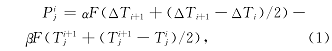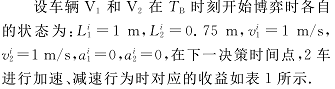上海交大杨明教授：基于博弈论的路口多车协作算法

厚势按：针对无交通灯十字路口，提出了一种基于博弈论的路口多智能车协作算法：

• 首先，利用场图工具建立路口车辆冲突模型；

• 然后，提出无交通灯十字路口冲突车辆的安全因素和时间因素的表达式，进而设计博弈的收益函数；

• 最后，针对冲突车辆设计了基于博弈论的协调算法，使用自主开发的智能车硬件仿真平台对提出的算法进行验证。

实验结果表明：提出的算法在保证车辆安全通过路口的同时，提高了路口的通行效率，降低了能源消耗。

本文来自 2011 年 11 月 11 日出版的《 华中科技大学学报（自然科学版）》，作者是来自上海交通大学自动化系的郭伟、杨明教授、王冰博士和上海交通大学机器人研究所的王春香副教授。

若想了解/回忆博弈论的基础知识，请阅读《 为什么说百度阿波罗画虎不成反类犬？| 厚势 》第 3.3 节。

路口存在许多可能导致事故发生的潜在冲突点，我国对国内城市的交通事故抽样统计表明：发生在平面交叉路口的交通事故率约为 30%。因此，寻找有效的路口协调控制方法，对改善路口通行效率、减少路口交通事故、提高整体交通安全水平均具有十分重要的意义。

目前，多采用交通灯协调不同方向车流的通行，当路口车流量很小时会导致路口车辆空等的现象，造成路口利用率低下。研究无交通灯路口场景下智能车辆的协调控制技术，能够达到保障路口通行安全，改善路口通行效率的目的。

路口多车协作算法主要有基于冲突表的协作算法 [1] 和基于可接受间隙理论的协作算法 [2] 等。本文针对上述问题，提出了基于博弈论的无交通灯路口多车协作控制算法，当路口车辆存在交通冲突时能通过速度控制防止碰撞，避免停车且提高通行效率。

1. 交叉路口冲突模型

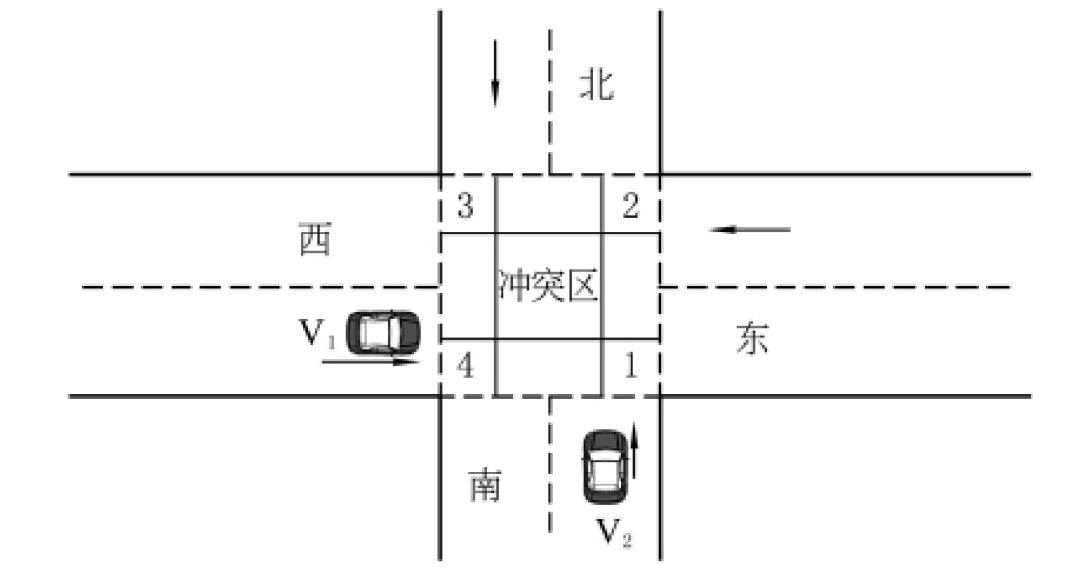
交通冲突 [3] 是一种可以被观察的现象，主要指 2 个或者多个道路使用者在时间和空间上不断靠近，若不改变其运动状态，则会发生碰撞。十字交叉路口存在多个冲突点，这里以自西向东行驶车辆 V1 与自南向北行驶车辆 V2 间的冲突点 1 为例进行分析，分析结果同样适用于路口其他冲突点。

图 1  十字交叉路口示意图

图 1 所示为简单的双向双车道十字交叉路口示意图，该交叉路口没有交通灯控制。为研究方便，本文对该交叉路口做以下假设：车辆通过路口过程中无行人和非机动车干扰；车辆行驶过程中所有车辆通信正常；各方向车辆均直行。

设图 1 中 V1 和 V2 分别为直行车辆，且其速度、加速度和距冲突点的距离分别为 v1，a1，L1 和 v2，a2，L2 ，1、2、3 和 4 为 4 个冲突点。V1 和 V2 通过路口时有 2 种情况：

• 2 车间存在交通冲突，保持当前行驶速度会导致两车发生碰撞；

• 2 车间不存在交通冲突，保持当前行驶速度２车不会发生碰撞。

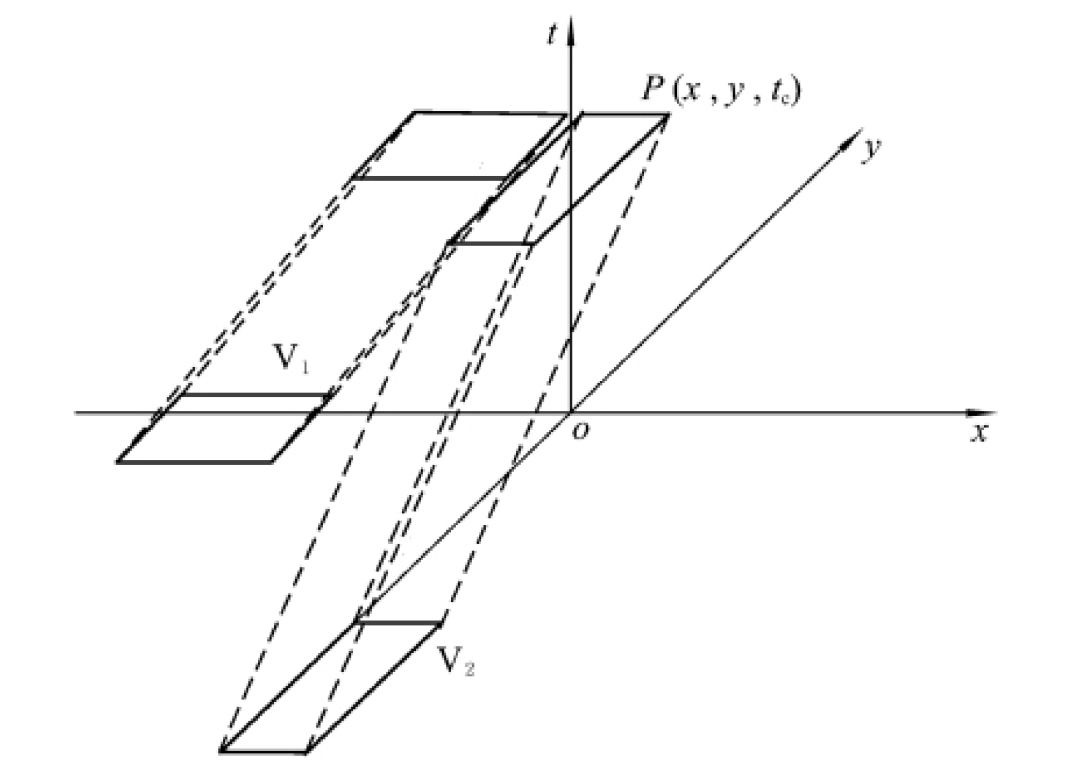
图 2  路口冲突车辆 VTF

为判断 2 车是否处于交通冲突状态，引入场图 [4] 工具来分析冲突判断过程。如图 2 所示，图中，xoy 坐标平面为车辆在地面的投影，包括车辆的外形和大小；t 轴为时间轴，t 轴的原点为当前时刻。若用场图描述车辆未来的运动轨迹，则称为虚拟轨迹场（VTF），这里采用 VTF 的方法预测 2 车未来的运动趋势 [5]，判断冲突状态。

若 2 车的虚拟轨迹场存在相交点 P(x,y,t_c)，则表示 2 车将发生冲突。根据冲突的定义，这意味着如果 2 车都不改变运动状态，那么在 t_c 时间后，2 车会在点（x，y）发生碰撞。 t_c 为碰撞时间，点（x，y）为潜在碰撞点。路口车辆不存在交通冲突时，车辆保持当前车速即可安全通过路口，因此主要分析当路口车辆存在冲突时的协调控制问题。在设计协调算法时，需要确定路口车辆的第一次决策时间点 TB 和最后一次决策时间点 TE，这里取车辆进入路口后第一次发现冲突车辆的时间点为  TB，判断 2 车冲突关系结束的时间点设为 TE。

2. 基于博弈论的协调算法

由有限次重复博弈定理可知，如果阶段博弈 G 有唯一的纯策略纳什均衡，那么，对于任意有限的次数Ｔ，重复博弈 G(T) 有唯一的子博弈精炼纳什均衡，其结果是阶段博弈 Ｇ 的纳什均衡重复 T 次 [6]。

博弈行为包括 3 个基本要素 [7]：

a. 参与者 Di 指博弈的决策主体，参与者的集合为 D = { D1，D2，…，D_N }；

b. 战略空间为 S = { S1，S2，…，S_N }，表示其中战略指参与者在给定信息集下的行动规则。每个参与者的战略形式化为 S_i： D_i → a_i（i = 1,2，…N），其中 a_i 为参与者 D_i 采取的行动；

c. 收益 P_i 指参与者 D_i 在 1 个特定的战略组合 { S1，S2，…，S_N } 下得到的期望收益。

定义博弈的参与者为车辆 V1 和 V2，2 车的战略空间为 S = { S1，S2 } ，其中，S1 ＝ S2 ＝｛加速，减速｝，2 车的收益分别为 P1(S1,S2) 和 P2 (S1,S2) 。将时间区间 [ TB,TE ] 划分为 N 个时间步，V1 和 V2 在每个时间步开始时同时行动。

在路口协作过程中，控制目标在保证车辆安全通过路口的前提下，以尽量少的时间通过十字路口。车辆决策时主要考虑安全因素和时间因素：安全因素指 2 车安全的通过路口，不会发生碰撞；时间因素指车辆以较短的时间通过路口。因此，应从这 2 方面分析，并设计车辆的收益函数。

2 车以第 i 个时间点的速度及加速度通过冲突点的时间差为：

根据上述分析，车辆 V1 和 V2 的收益函数可表示为：

式中：F(·) 为归一化计算；且 α 和 β 分别为安全因素和时间因素的权重系数，α + β =1 。由于路口协作控制的预期是在安全通过的前提下尽可能快速通过路口，因此式 (1) 能正确反映博弈收益。

3. 实验结果分析

采用自主研发的智能车硬件仿真实验平台对算法进行验证。该平台使用的车模是真实车辆的微缩，对车辆的仿真具有很好的现实意义。

实验环境为宽度为 1.5 m 的十字路口，2 实验车辆以 1m/s 的速度匀速在十字路口交叉通行。博弈过程中车辆加速行为时，加速度为 0.5 m/s^2 ，减速行为时，加速度为 -0.5 m/s^2，α = 0.5，β = 0.5。

由表 1 可知，阶段博弈存在唯一纳什均衡（0.3282,0.8048）。根据有限次重复博弈定理可知，有限次重复博弈有唯一的子博弈精炼纳什均衡，其结果是阶段博弈的纳什均衡重复 T 次，即在整个博弈过程中 2 车会延续第一次阶段博弈时 2 车的行为。

表 1  阶段博弈过程中纳什均衡

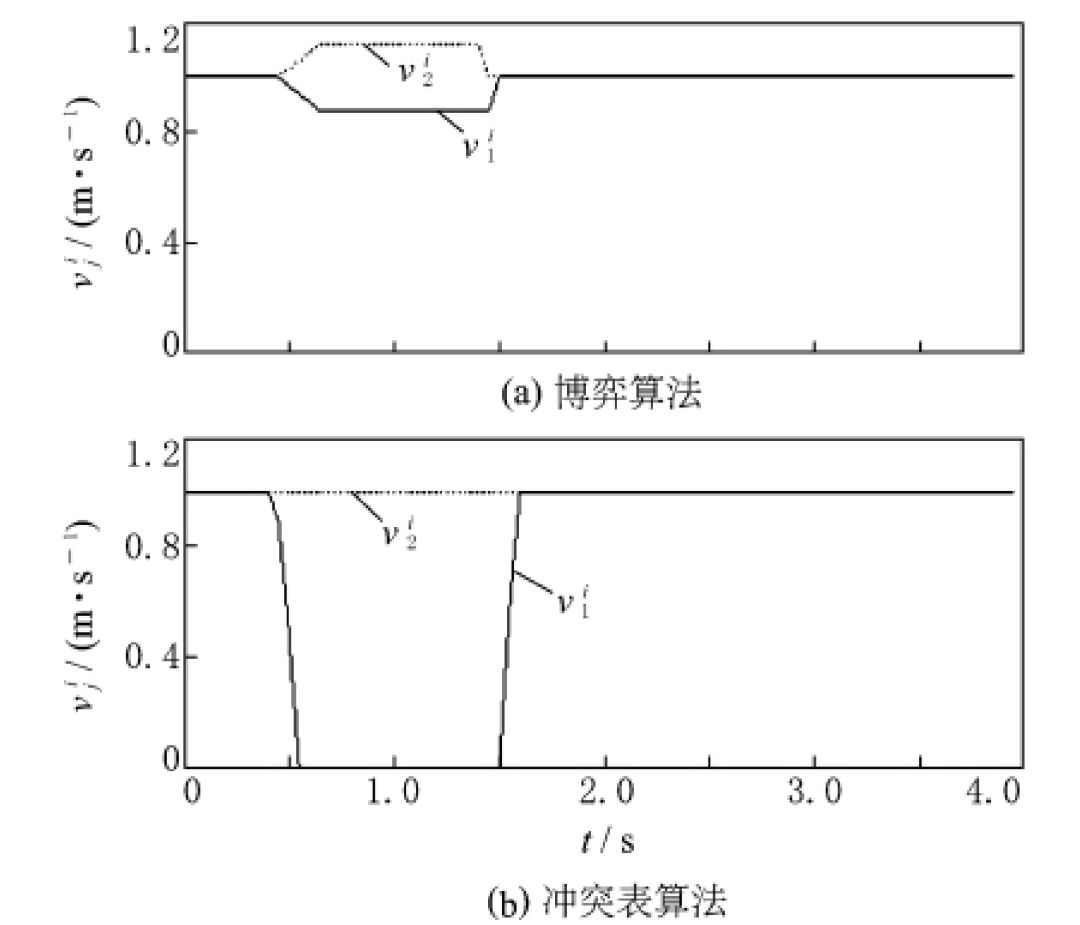
图 3  基于 2 种控制算法的车速对比

为验证本文算法的高效性，选择基于冲突表的路口协作算法作为对比，对 2 种算法分别进行实验，实验结果如图 3 和 4 所示，图中 t 为时间。

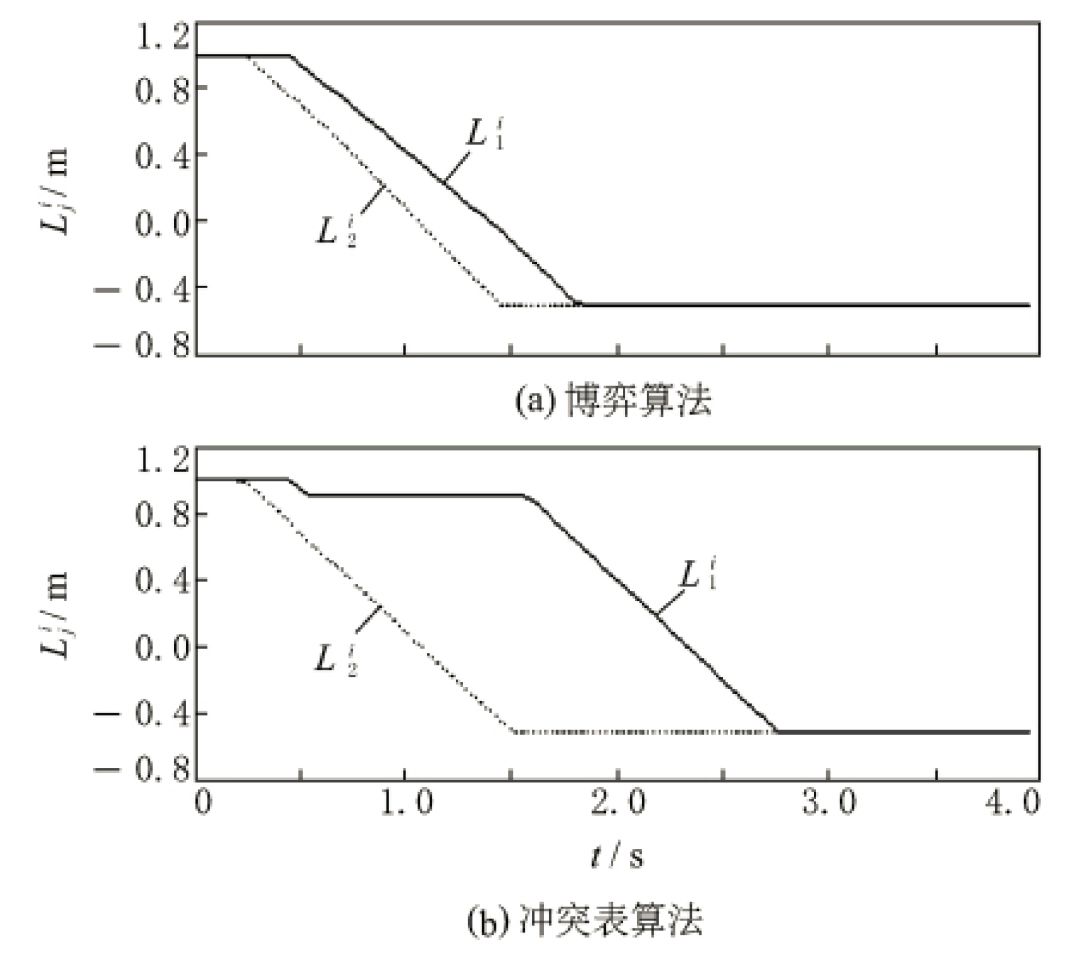
图 4  基于 2 种控制算法距冲突点的距离对比

为直观表示出车辆通过路口的时间，图 4 中只给出在路口区域内（距冲突点距离在 -0.5 ~ 1 m 之间）车辆距冲突点距离的变化，在路口区域外视为车辆距离冲突点始终为 1m 和 -0.5 m。

由图 4 可见：采用本文算法时，冲突车辆全部通过路口所用的时间明显小于采用冲突表算法所用的时间，可见本文算法能提高冲突车辆通过路口的效率。

从实验结果可以看出：

• 采用本文算法，在路口车辆存在交通冲突时能通过速度控制实现避让；

• 而采用冲突表算法则需要车辆在路口停车等待冲突车辆通过路口，本文算法可以使车辆更早通过路口，提高路口的通行效率，降低了车辆启动过程中的能源消耗。

编辑整理：厚势分析师伊龙马

转载请注明来自厚势和厚势公号：iHoushi

-END-

文章精选

企业家

马斯克和贾跃亭 ｜福特CEO下台｜正道汽车仰融

任正非裁员｜电池大牛凯尔提离开特斯拉

智能驾驶

BBC自动驾驶纪录片｜自动驾驶第一案，谷歌讼Uber

高精地图｜自动驾驶的灾难｜英特尔收购Mobileye

清华汽车李客强教授：智能车辆运动控制研究综述

Mobileye创始人：无人驾驶汽车如何自证清白？

智能电动汽车的感知、决策与控制等关键基础问题及对策研究

北理工：一种评价无人驾驶车辆智能水平的新方法

埃森哲：汽车保险业如何应对自动驾驶的到来？

新能源汽车

全国50个新能源汽车项目大盘点

锂电池发展趋势｜中国汽车产业电动化进程

苹果收购特斯拉？｜丰田和特斯拉决裂

中科院物理所：电动汽车动力电池技术研究进展

电动汽车共享商业模式的发展

一文了解电动汽车无线充电技术及其商业应用

项目和评论

以色列最强10家自动驾驶创业公司

 37个汽车分时项目盘点｜百度投资蔚来汽车

马化腾或为共享单车最大赢家｜汽车产业3大趋势

Momenta获$4000万B轮

百度系自动驾驶初创公司 Pony.ai 的突围之路

这些大神从Google出走，创办了五家（命运各异的）无人车公司

戴世智能带你读懂自动驾驶高精度行车定位技术

厚

势

汽

车

为您对接资本和产业

新能源汽车 自动驾驶 车联网

联系邮箱

bp@ihoushi.com

点击阅读原文，查看文章「官宣！上汽与蔚来获准上路测试自动驾驶汽车 」