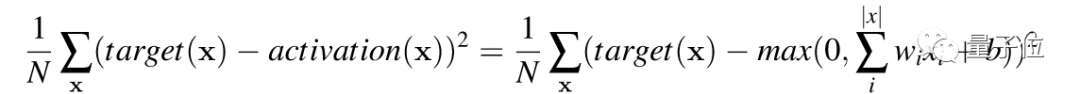一文读懂深度学习中的矩阵微积分，fast.ai创始人&ANTLR之父出品 | 免费资源

鱼羊 编译整理
量子位 报道 | 公众号 QbitAI

想要真正了解深度神经网络是如何训练的，免不了从矩阵微积分说起。

虽然网络上已经有不少关于多元微积分和线性代数的在线资料，但它们通常都被视作两门独立的课程，资料相对孤立，也相对晦涩。

不过，先别打退堂鼓，来自旧金山大学的Terence Parr教授说：矩阵微积分真的没有那么难。

这位ANTLR之父和fast.ai创始人Jeremy Howard一起推出了一篇免费教程，旨在帮你快速入门深度学习中的矩阵微积分。简明，易懂。

DeepMind研究科学家Andrew Trask评价说：

如果你想跳过不相干的内容，一文看尽深度学习中所需的数学知识，那么就是这份资源没错了。

只需一点关于微积分和神经网络的基础知识，就能单刀直入，开始以下的学习啦。

深度学习所需的矩阵微积分

先来看一眼这篇教程都涵盖了哪些内容：

• 基本概念

• 矩阵微积分

• 神经元激活的梯度

• 神经网络损失函数的梯度

文章开篇，先介绍了一下人工神经元。
          

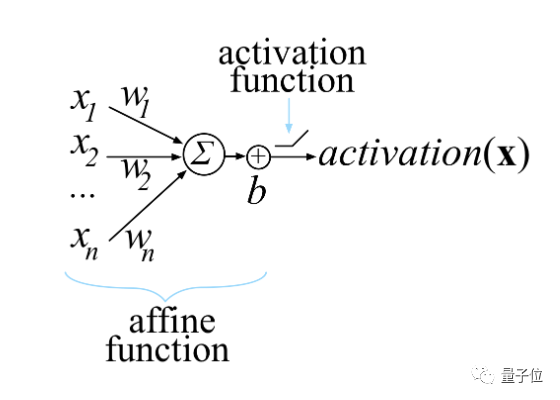
神经网络中单个计算单元的激活函数，通常使用权重向量w与输入向量x的点积来计算。

神经网络由许多这样的单位组成。它们被组织成称为层的神经元集合。上一层单元的激活成为下一层单元的输入，最后一层中一个或多个单元的激活称为网络输出。

训练神经元意味着对权重w和偏差b的选择。我们的目标是逐步调整w和b，使总损失函数在所有输入x上都保持较小。

导数规则、向量计算、偏导数……复习完需要掌握的先导知识，文章开始进入重要规则的推导，这些规则涉及矢量偏导数的计算，是神经网络训练的基础。

比如在矩阵微积分这一节中，涵盖：

• 雅可比式（Jacobian）的推广

• 向量element-wise二元算子的导数

• 涉及标量展开的导数

• 向量和降维

• 链式法则

每一小节中，都有简洁明了的示例，由浅入深，层层递进。

如果你在学习的过程中遇到不理解的地方，不要着急，耐心返回上一节阅读，重新演算一下文中的示例，或许就能理顺思路。

如果实在是卡住了无法推进，你还可以在fast.ai论坛（链接见文末）的“Theory”分类下提问，向Parr和Howard本人求解答。

而在文章的末尾，作者附上了所有数学符号的对照表。

以及重点概念的详细补充信息。

值得注意的是，Parr和Howard也强调了，与其他学术方法不同，他们强烈建议先学会如何训练和使用神经网络，然后再深入了解背后的基础数学。因为有了实践经验，数学会变得刚容易理解。

传送门

网页版：
https://explained.ai/matrix-calculus/index.html

PDF：
https://arxiv.org/abs/1802.01528

fast.ai论坛：
http://forums.fast.ai/

作者系网易新闻·网易号“各有态度”签约作者

— 完 —

大咖齐聚！参会嘉宾重磅揭晓

量子位 MEET 2020 智能未来大会启幕，李开复、倪光南、景鲲、周伯文、吴明辉、曹旭东、叶杰平、唐文斌、王砚峰、黄刚、马原等AI大咖与你一起读懂人工智能。观众票即将售罄，扫码报名预定席位 ~

量子位 QbitAI · 头条号签约作者

վ'ᴗ' ի 追踪AI技术和产品新动态

喜欢就点「在看」吧 !