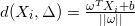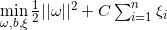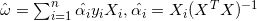数据分析师应该知道的16种回归方法：支持向量回归

2018 年 9 月 3 日 数萃大数据

支持向量回归(SVR)的工作原则类似与支持向量机(SVM)，可以说SVR是SVM在因变量为数值变量或连续变量情况下的应用。SVM的主要思想是：给定训练样本，建立一个超平面作为决策曲面，使得正例和负例之间的间隔最大化。SVR的基本思想是：让所有样本点逼近超平面，使得样本点到超平面的总偏差达到最小。同简单线性回归(SLR)相比,SVR不要求变量间的高斯-马尔科夫假设，仅依赖于核函数。SVR的另一个优势是：它允许在不改变解释变量的情况下构建非线性模型，因而可以更好地解释生成的模型。下面开始介绍SVR及其在R中的实现。

首先考虑简单二分类问题。设,为样本向量，根据SVM的的基本思想，构建模型：

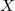
其中为样本向量的法向量，为偏移常量。因此，样本空间可通过如下超平面分割：

样本点到距离为：

如果这个问题是线性可分的(即在当前空间存在一个超平面可以把正负例样本分开)，就会存在无数解。为此我们考虑

下面开始寻找分割最大间隔(即使上图中的淡黄色区域达到最大)，我们需要解决如下优化问题：

object:

subject to:

直接对上述目标函数优化一般不存在有效解。我们考虑形最小间隔为1的情形即,此时上述带约束优化问题变为：

object:

subject to:

为了便于计算，将上述目标函数写为：

在实际问题中，训练集也可能会出现不可分的样本点（称为离群点），它们会影响分类超平面的形成。为处理不可分离的数据点，可引入松弛变量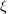，用于度量数据点对模式可分理想条件的偏离程度。此时，最优化问题变为：

object:

subject to:

为惩罚因子,,越大，对目标函数的损失也越大，此时就暗示着你非常不愿意放弃这些离群点，最极端的情况是你把定为无限大，这样只要稍有一个点离群，目标函数的值马上变成无限大，马上让问题变成无解。

对于上述线性可分和线性不可分的最优化问题，可以采用拉格朗日乘子法来求解。对于线性可分情况，添加拉格朗日乘子,其拉格朗日量为：

考虑上式的对偶问题

object:

subject to:

其中

对于线性不可分情形，添加拉格朗日乘子,其拉格朗日量为：

其对偶问题

object:

subject to:

其中

上述两个问题都转化为二次规划问题，因此存在全局最优解。这两个问题的最优解都为：

对比OLS，则SVR的预测值为：

对于非线性问题，超平面已经无法进行分类，可通过核函数将线性不可分问题转化成高维空间的线性问题，接收低维空间的输入值，然后计算出高维空间的内积值。对于非线性SVR问题，将线性SVR中内积用核函数替代即可。目前常用的核函数有：

高斯核
- 多项式核
- 线性核
- Laplacian核

案例

本案例使用pressure数据集，该数据集描述摄氏温度和水银蒸汽压之间的关系如下图所示

SVR使用e1071包，KSVR使用kernlab，下图绘制了四种KSVR与原始SVR的拟合曲线，出线性KSVR外，其余KSVR通过调谐参数都可以很好对数据进行拟合，而且优于SVR。

  
  
    
   
   
     cols=RColorBrewer::brewer.pal(8,'Dark2')
   
   
     plot(pressure$temperature,pressure$pressure,pch=16,cex=2,col='gray70',
   
   
          xlab='temperature',ylab='pressure')
   
   
     library(e1071)
   
   
     modelsvm = svm(pressure~temperature,pressure)
   
   
     predsvm = predict(modelsvm, pressure)
   
   
     lines(pressure$temperature, predsvm, col = cols[1], lty=1,lwd=2)
   
   
     
   
   
     library(kernlab)
   
   
     test1 <- ksvm(pressure~temperature,data=pressure,kernel="rbfdot",
   
   
                   kpar=list(sigma=0.5),C=50,cross=3)
   
   
     predksvm1 = predict(test1, pressure)
   
   
     lines(pressure$temperature, predksvm1, col = cols[2], lty=1,lwd=2)
   
   
     
   
   
     test2 <- ksvm(pressure~temperature,data=pressure,kernel="polydot",
   
   
                   kpar=list(degree=3, scale=1, offset=1 ),C=5,cross=3)
   
   
     predksvm2 = predict(test2, pressure)
   
   
     lines(pressure$temperature, predksvm2, col = cols[3], lty=1,lwd=2)
   
   
     
   
   
     test3 <- ksvm(pressure~temperature,data=pressure,kernel="laplacedot",
   
   
                   kpar=list(sigma = 2),C=5,cross=3)
   
   
     predksvm3 = predict(test3, pressure)
   
   
     lines(pressure$temperature, predksvm3, col = cols[4], lty=1,lwd=2)
   
   
     
   
   
     linepot <- function(x,y) {sqrt(sum((x-y)^2))}
   
   
     class(linepot) <- "kernel"
   
   
     test4 <- ksvm(pressure~temperature,data=pressure,kernel=linepot
   
   
                   ,C=5,cross=3)
   
   
     predksvm4 = predict(test4, pressure)
   
   
     lines(pressure$temperature, predksvm4, col = cols[5], lty=1,lwd=2)
   
   
     
   
   
     legend('topleft',c('SVR','kSVR(gauss)','kSVR(poly)','kSVR(laplace)',
   
   
                        'kSVR(line)'),col= cols[1:5],lty=1,lwd=2,bty='n')