在机器学习中，支持向量机（SVM，也称为支持向量网络）是带有相关学习算法的监督学习模型，该算法分析用于分类和回归分析的数据。支持向量机（SVM）算法是一种流行的机器学习工具，可为分类和回归问题提供解决方案。给定一组训练示例，每个训练示例都标记为属于两个类别中的一个或另一个，则SVM训练算法会构建一个模型，该模型将新示例分配给一个类别或另一个类别，使其成为非概率二进制线性分类器（尽管方法存在诸如Platt缩放的问题，以便在概率分类设置中使用SVM）。SVM模型是将示例表示为空间中的点，并进行了映射，以使各个类别的示例被尽可能宽的明显间隙分开。然后，将新示例映射到相同的空间，并根据它们落入的间隙的侧面来预测属于一个类别。

知识荟萃

支持向量机 SVM

基础入门

1.是-sklearn库官方介绍英文版作者：开源库 http://scikit-learn.org/stable/modules/svm.html

可参照官方教材进行学习，适合有一定英语基础，对sklearn有更深认识。

2.scikit-learn 0.18 中文文档作者：ApacheCN Apache中文网 http://cwiki.apachecn.org/pages/viewpage.action?pageId=10030181

中文教材，参照上面的英文教材一起学习。

3.支持向量机（SVM）居然是这种机作者：王大宝的CD http://blog.csdn.net/sinat_22594309/article/details/61615946

描述：今天想说的呢是SVM支持向量机（support vector machine），我觉得这个算法它初始出发的想法真的是非常符合人性，特征空间上间隔最大的分类器，你随便问一个人分开空间上的两坨点最佳的平面是什么，他的直觉也会告诉他是介于两坨之间然后比较中间的那个位置，如果不说人话，那就是SVM。

4.手把手教你实现SVM算法（一）作者：自在逍遥 http://blog.csdn.net/alvine008/article/details/9097105

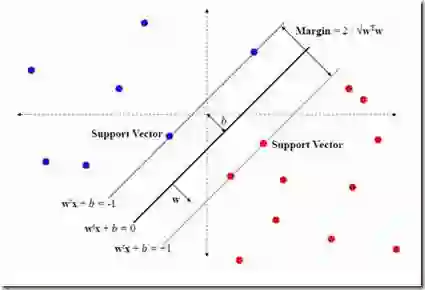
描述：SVM从线性可分情况下的最优分类面发展而来。最优分类面就是要求分类线不但能将两类正确分开(训练错误率为0),且使分类间隔最大。SVM考虑寻找一个满足分类要求的超平面,并且使训练集中的点距离分类面尽可能的远,也就是寻找一个分类面使它两侧的空白区域(margin)最大。

5.手把手教你实现SVM算法（二）作者：自在逍遥 http://blog.csdn.net/alvine008/article/details/9097111

描述：SMO算法和以往的一些SVM改进算法一样，是把整个二次规划问题分解为很多较易处理的小问题，所不同的是，只有SMO算法把问题分解到可能达到的最小规模：每次优化只处理两个样本的优化问题，并且用解析的方法进行处理。我们将会看到，这种与众不同的方法带来了一系列不可比拟的优势。

6.支持向量机通俗导论（理解SVM的三层境界）作者：v_JULY_v http://blog.csdn.net/v_july_v/article/details/7624837

描述：OK，此文从最初2012年5月开始动笔，到后续不断的修改，创造了三个之最，即所写时间最长，所花心血最大，所改次数最多，因为我的目标是让没有任何机器学习基础的都能看懂此文，所以总是不停的改，不停的改，不想放过任何一个小的细节。再者，引用侯捷的一句话是：天下大作，必作于细。

7.SVM理解作者：viewcode http://blog.csdn.net/viewcode/article/details/12840405

描述：SVM的文章介绍多如牛毛，很多介绍都非常详尽，而我却一点都不开窍，始终无法理解其中的奥秘。这次，我要用自己粗浅的语言，来撩开我与SVM之间的面纱

8.Stanford机器学习---第八讲. 支持向量机SVM 作者：Rachel-Zhang http://blog.csdn.net/abcjennifer/article/details/7849812/

描述：本章内容为支持向量机Support Vector Machine（SVM）的导论性讲解，在一般机器学习模型的理解上，引入SVM的概念。原先很多人，也包括我自己觉得SVM是个很神奇的概念，读完本文你会觉得，其实只是拥有不同的目标函数，不同的模型而已，Machine Learning的本质还没有变，呵呵~ 完成本文花了我很长时间，为了搞懂后面还有程序方便和参考网站大家实验，希望对大家有所帮助。

9.支持向量机（SVM）的详细推导过程及注解（一）作者：风之忧伤 http://blog.sina.com.cn/s/blog_4298002e010144k8.html

描述：支持向量机的原理很简单，就是VC维理论和最小化结构风险。在阅读相关论文的时候，发现很多文章都语焉不详，就连《A Tutorial on Support Vector Machines for Pattern Recognition》这篇文章对拉格朗日条件极值问题的对偶变换都只是一笔带过，让很多人觉得很困惑。下面我将就SVM对线性可分的情况作详尽的推导。

10.开发者自述：我是怎样理解支持向量机（SVM）与神经网络的作者：AI研习社 https://www.leiphone.com/news/201705/v10u2BOvGHEbzBpV.html

描述：支持向量机并不是神经网络，这两个完全是两条不一样的路吧。不过详细来说，线性SVM的计算部分就像一个单层的神经网络一样，而非线性SVM就完全和神经网络不一样了（是的没错，现实生活中大多问题是非线性的）

11.机器学习之旅---SVM分类器作者：taotao1233 http://blog.csdn.net/jinshengtao/article/details/40900865

描述：本次内容主要讲解什么是支持向量，SVM分类是如何推导的，最小序列SMO算法部分推导。最后给出线性和非线性2分类问题的smo算法matlab实现代码。

12.程序员训练机器学习 SVM算法分享作者：Greg Lamp http://www.csdn.net/article/2012-12-28/2813275-Support-Vector-Machine

描述：支持向量机（Support Vector Machine）已经成为一种非常受欢迎的算法。在这篇文章里，Greg Lamp简单解释了它是如何进行工作的，同时他也给出了使用Python Scikits库的几个示例。所有代码在Github上都是可用的，Greg Lamp以后还会对使用Scikits以及Sklearn的细节问题进行更深一步的阐述。CSDN对本篇技术性文章进行了编译整理：