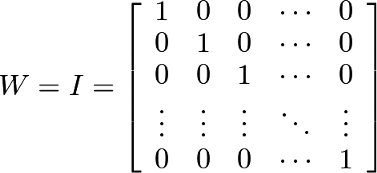如何优化深度神经网络?

训练一个深度神经网络并使其获取最佳的性能是一件具有挑战的任务。
原标题 | Optimization Problem in Deep Neural Networks
翻译 | Ryan(西安理工大学)、肖书忠(深信服)
编辑 | Pita (注:相关链接可点击阅读原文访问)
训练一个深度神经网络并使其获取最佳的性能是一件具有挑战的任务。在本文中,我将会探索这项任务中最常见的问题及其解决方案。这些任务中包括网络训练时间过长,梯度消失与爆炸,还有网络初始化方法等问题,这些我们在此统称为优化问题。至于其余在训练网络中出现的问题则认为是正则化问题,我在之前的文章中已经讨论过了。如果你现在并没有阅读过它,请先阅读前文:
Improving Deep Neural Networks (https://towardsdatascience.com/improving-deep-neural-networks-b5984e29e336)
输入数据 标准化
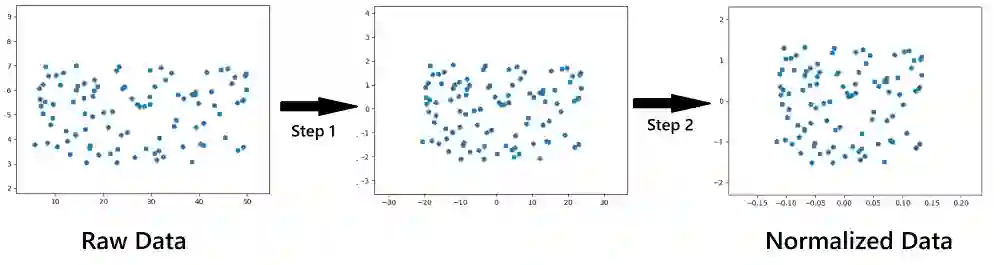
当我们在训练神经网络时,我们可能会注意到模型训练的时间比预期的要久。这是因为输入数据没有进行标准化,让我们尝试通过下方仅有两个特征的输入数据来理解标准化的含义。
在原始数据中,数据的X轴(特征X)取值区间为5-50,Y轴(特征Y)取值区间为3-7。另一方面,在标准化后的数据中,X轴取值区间时-0.15~0.15, Y轴的取值区间时-1.5~1.5。
通过标准化数据,我们缩放后的特征值范围与原始数据类似:而标准化数据只需要两步过程。
通过将数据减去其均值,使得数据的均值为0,并让其除以其方差,得到标准化数据。
mu = np.mean(X)X = X - musigma = np.linalg.norm(X)X = X/sigma
这里有一点需要注意,我们需要使用同样的均值和方差去转换我们的测试数据,因为我们想用同样的方法来缩放它们。
为什么标准化会起作用呢?
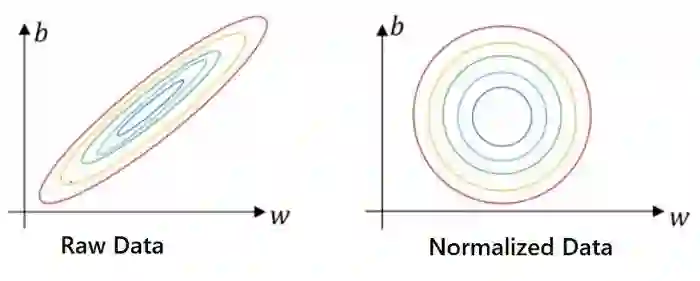
既然我们已经知道了如何标准化数据集,那么让我们试着理解为什么标准化适用于下面的示例。下面是代价值J,权重W和偏差b之间的等高线图。中心表示我们必须达到的最小代价。
右边的图看起来更对称,这是标准化背后工作原理的关键。
如果特征的范围差异很大,则不同权重的值也会有很大的差异,并且将花费更多的时间来选择完美的权重集。然而,如果我们使用标准化数据,那么权重就不会有很大的变化,我们将在较短的时间内获得理想的权重集。
此外,如果使用原始数据,则必须使用较低的学习率来适应不同的等高线高度。但是在归一化数据的情况下,我们有更多的球面轮廓,通过选择更大的学习速率,我们可以直接达到最小值。
当特征在相似的尺度上时,优化权重和偏差变得容易。
梯度消失和梯度爆炸
梯度消失和梯度爆炸问题源于权值的初始化。以上两个问题都导致网络的训练不当和较慢。正如他们的名字所暗示的那样,当权重消失并最终变得太小时,会出现梯度消失;而在梯度爆炸时,权重会爆炸并变得过大。让我们在一个例子的帮助下更好地理解它们。
设W 是与单位矩阵 I 相近的所有层的权重矩阵。
在前向传播中,一个特定层的输出 Z 由以下公式定义,其中 W 是权重矩阵,X 是输入,b 是偏差:
如果我们在 L 层(L 为层数)上执行上述计算,那么我们可以假设权重矩阵 W 将乘以 L 次,忽略偏差。
现在,如果一个大于1的特定值,例如1.5,则层的激活将呈指数递增,梯度将变大的,并且梯度下降将采取大的步长,网络将花费很长时间来达到最小值。这种问题被称为梯度爆炸。
同样的,如果一个小于1的特定值,例如0.9,则层的激活将呈指数递减,梯度将变得很小,并且梯度下降将采取小的步长,网络将需要很长时间才能达到最小值。这种问题被称为梯度消失。
为了避免梯度爆炸和梯度消失的问题,我们应该遵循以下规则 :
1. 激活层的均值应该为0
2. 激活层的方差应该在每一层都保持不变。
如果遵循上述规则,则确保梯度下降不会采取太大或太小的步长,并以有序的方式向最小值方向移动,避免了梯度爆炸和梯度消失。这也意味着网络将以更快的速度进行训练和优化。由于问题的根源在于权值的初始化不当,所以我们可以通过正确地初始化权值来解决这个问题。
Xavier 初始化
当特定层的激活函数为 Tanh 时,使用Xavier初始化。我们可以按照以下方式使用Xavier初始化:
# Let the dimesnion of weight matrix be(5,3)# The variance is(1/neurons in previous layer)# Randn ensure that the mean = 0W = np.random.randn(5,3) * np.sqrt(1/3))
He 初始化
当特定层的激活函数为 ReLU 时,使用 He初始化。我们可以通过以下方式使用 He初始化:
# Let the shape of the weight matrix be(5,3)# The variance is(2/neurons in previous layer)# Randn ensure that the mean = 0W = np.random.randn(5,3) * np.sqrt(2/3))
参考文献
1. Deep Learning Notes(http://www.deeplearning.ai/ai-notes/initialization/)
2. Coursera — Deep Learning Course 2(https://www.coursera.org/learn/deep-neural-network/home/welcome)
感谢阅读这篇文章的读者,如果您有任何问题或疑问,欢迎在下面的评论部分提问。我非常乐意回答并帮助你。如果你喜欢这个文章,我将定期更新一个新的文章,欢迎大家来阅读。欢迎读者提出任何能改善我的文章的建议。
访问本文相关链接,可点击底部阅读原文或用浏览器打开以下地址访问:
https://ai.yanxishe.com/page/TextTranslation/1918
via https://medium.com/analytics-vidhya/optimization-problem-in-deep-neural-networks-400f853af406