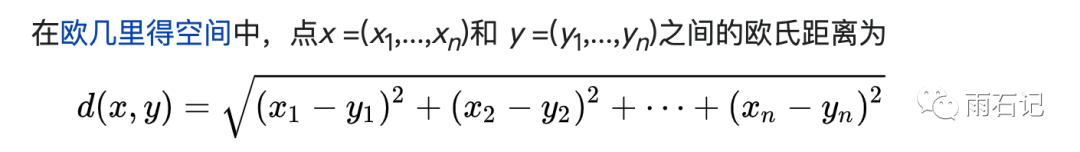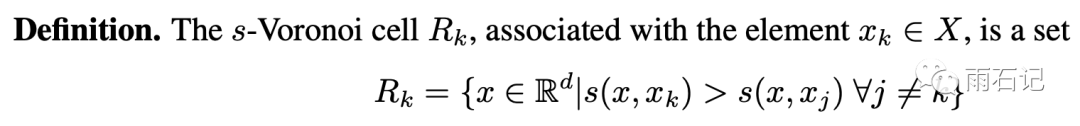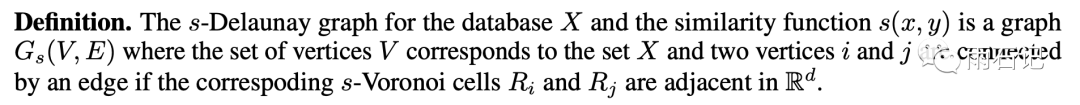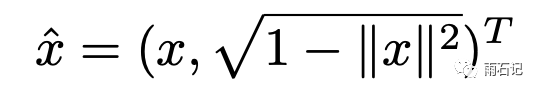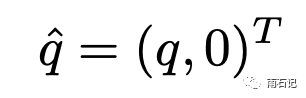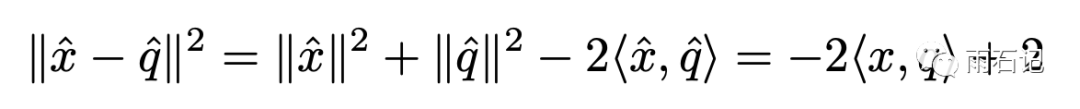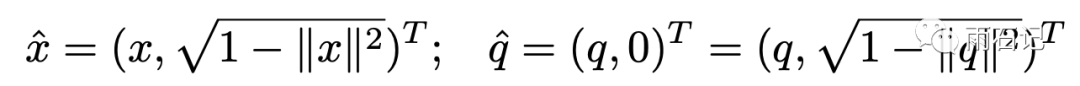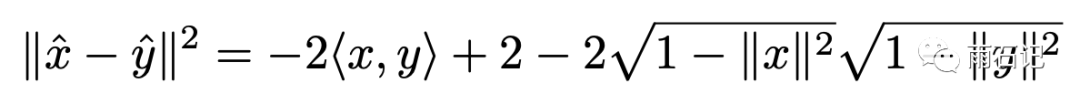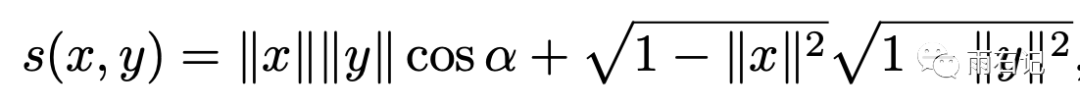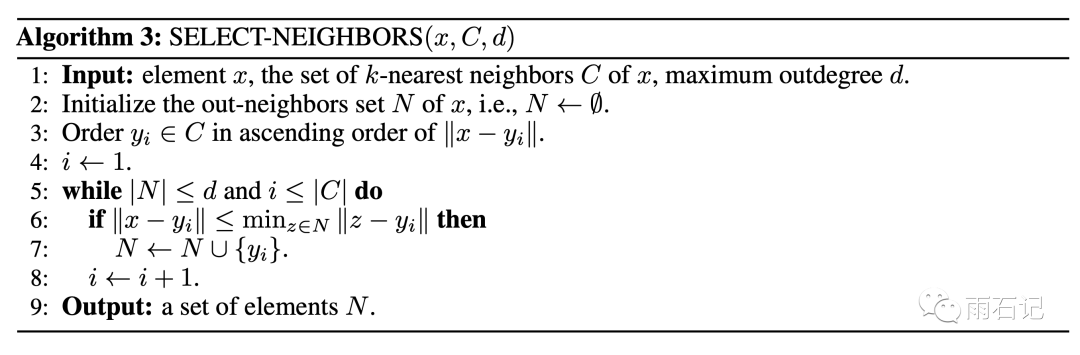基于Delaunay图的快速最大内积搜索算法

2020 年 9 月 25 日 AINLP

本文是参考文献[1-5]的知识点总结。

最大内积搜索算法，英文是Maximum Inner Product Search，简称MIPS。

我们在之前分别介绍过百度的点击率预估和阿里的推荐算法：

随着深度学习的广泛使用，越来越多的样本被表达成embedding，因而，在很多服务中，寻找Top-K内积向量的需求也越来越多，比如上面链接中百度的广告搜索业务，阿里的电商业务等。更广泛的，在很多NLP任务中也需要快速内积搜索算法，比如Bert系列的Reformer，语言模型中的下一个词语预测等。

那么在大规模数据的条件下，如何进行快速的最大内积搜索呢？暴力算法自然是直接遍历，时间复杂度是O(nd)，n是样本数，d是样本维度。但显然，在样本过亿甚至过十亿的数据下，线性算法是无法达到毫秒级的延迟需求的。

目前主流的方法如下几种：

局部敏感哈希，用哈希函数对样本进行压缩和索引，方便快速找到。
基于内积上界去做过滤，典型的方法如Cauchy-Schwarz不等性。这一点暂时先不关注。
将MIPS问题给转化成最近邻搜索NNS(Nearest Neighbor Search)问题，这样就可以采用NNS上的方法，包括基于图的搜索以及基于哈希的搜索等。
直接将NNS上的方法应用在MIPS上。

本文主要展开讲后两点的方法。

层次化德劳内图

在上一部分，有一个关于在已有的点上找最近的M个点的操作的讨论。即有些跨度较大的边能起到高速公路的效果。但这点是没有保证的，效果好还是不好依赖于shuffle的结果，有点看天吃饭的意思。

然后在搜索的时候，如何决定走向也是不明确的，为了能先走跨度大的路径，需要依赖点的边的数目来计算这个点是不是跨度大的边上的点，然后决定走不走这条边，所有的这些使得贪心遍历有了太多的预设，算法复杂且不一定好。

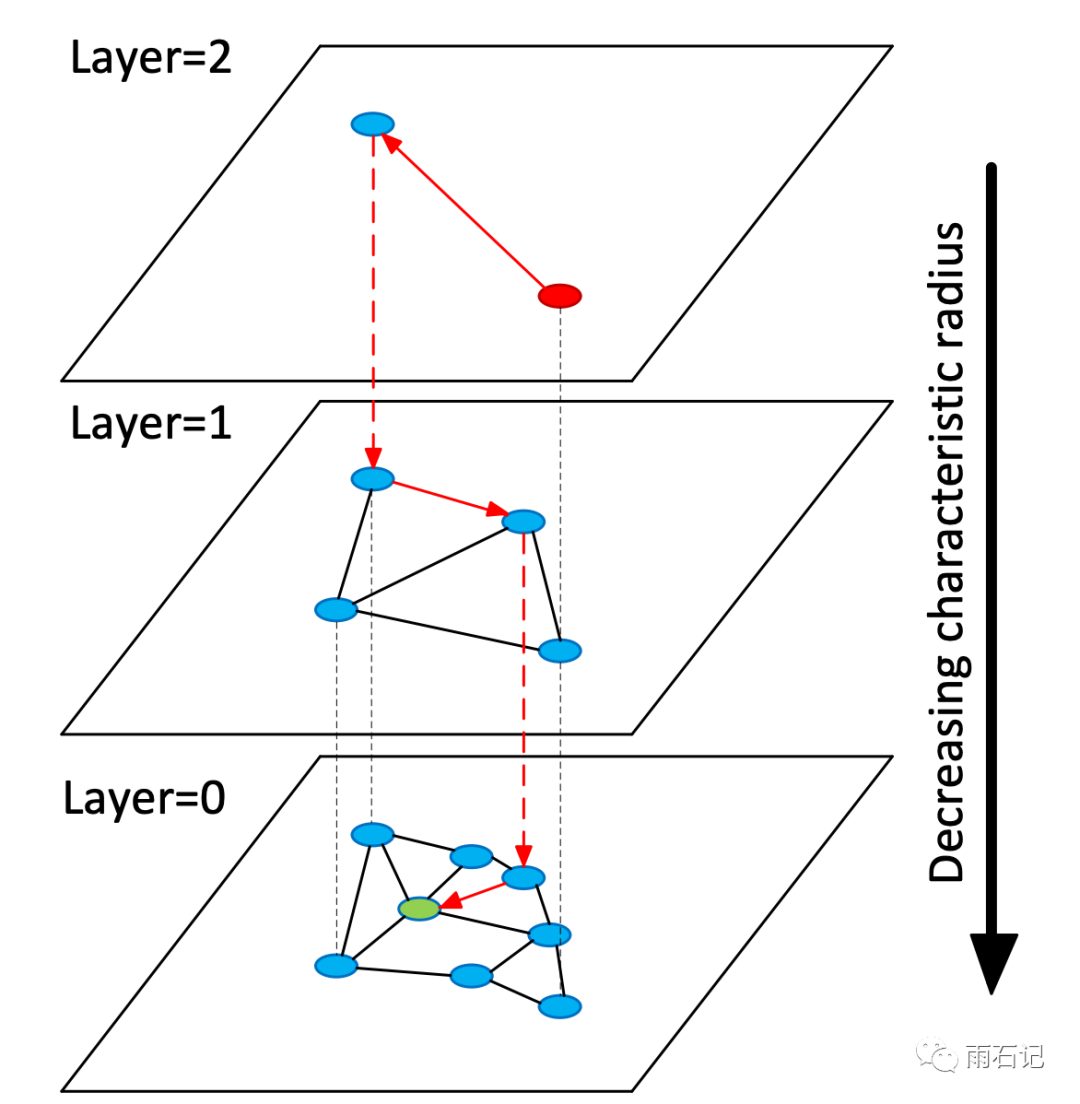
所以就有了层次化的德劳内图如下：

根据距离的大小，在不同的距离范围内构建多层德劳内图，这样，跨度大的搜索和跨度小的搜索可以分开。破了看天吃饭的壁，输入数据点前也不用shuffle了。在遍历的时候，先在跨度大的层次上遍历，一定程度后就下沉一层继续遍历，直到最后。

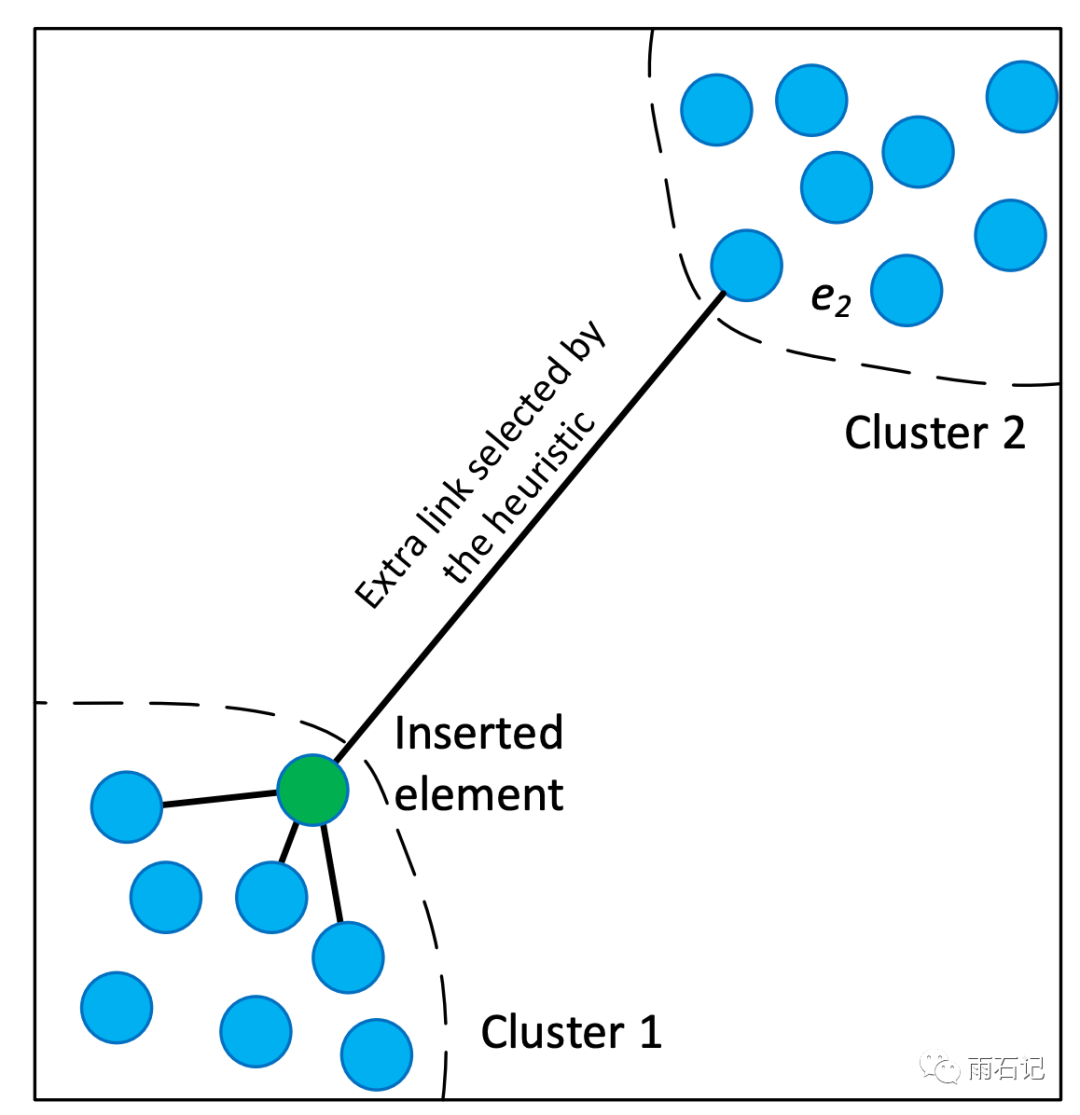
另外，为了防止数据不同簇之间内卷，还需要基于启发式的添加一些特殊的边：

不同簇之间要有一定的边连接才能保证数据都被reach到。

以上是参考论文[3]的主要内容，这里忽略了很多实现的细节，感兴趣的可以去看论文原文。

将MIPS转化为NNS

转化的方法其实不难，看下面三个公式还有两个限制，将x和q进行变换

变化后的x和q去做l2-norm就跟做内积是等价的。

这样的变换要求||x||<=1， ||q||= 1。这样能推出变换后的x和q的norm值是1。

但显然，我们通过同比例缩放x和q可以达到||x||<=1,但||q||在缩放后未必是1。变换后的q不为1就导致了上面的等价公式不一定成立。

于是，我们再泛化一下，让||q||也<=1，x和q的变化如下：

变换后的x和q做内积如下：

根据余弦定理，还可以继续转化：

这个公式就很有意思了，为什么呢？因为这个余弦系数，随着维度的增高，临近的点的余弦值会变得很越来越小，导致这个公式很容易被后一项所主导，而前一项才是我们所关注的。

这也就解释了为什么将MIPS问题转化成NNS会有问题。

本部分内容来自于论文[1].

基于内积的德劳内图——ip-Delaunay

那我们该怎么办呢？我们在最近邻搜索中使用的Metric计算方法是-||x-y||，我们可以直接换成<x, y>内积吗？

以下是定理和证明：

我们要论证的是内积德劳内图中的局部极值就是全局极值。

这个论证是反证法论证。我不带公式的试着翻译：假如一个点是局部极值，那么假设它不是全局极值，那么必然另外存在一个全局极值。此时如果我把局部极值点以及它的相邻点还有这个全局极值点之外的所有点都删掉。那么整个空间必定被局部极值点还有相邻点的沃罗诺伊块塞满，全局极值点也必属于其中一个，那么这就说明局部极值点不是极值点，因为相邻的沃罗诺伊块内有个跟query距离更小的点。矛盾，所以得证。

有了这个证明之后，就能推出在内积德劳内图上也能通过贪心游走的算法得到最后的结果。

还有一个更有意思的推论。

这个推论的含义是如果metric计算是线性的(内积计算就是线性的)，那么如果两个点是极值点，那么这两个点上的任何一点就是极值点。

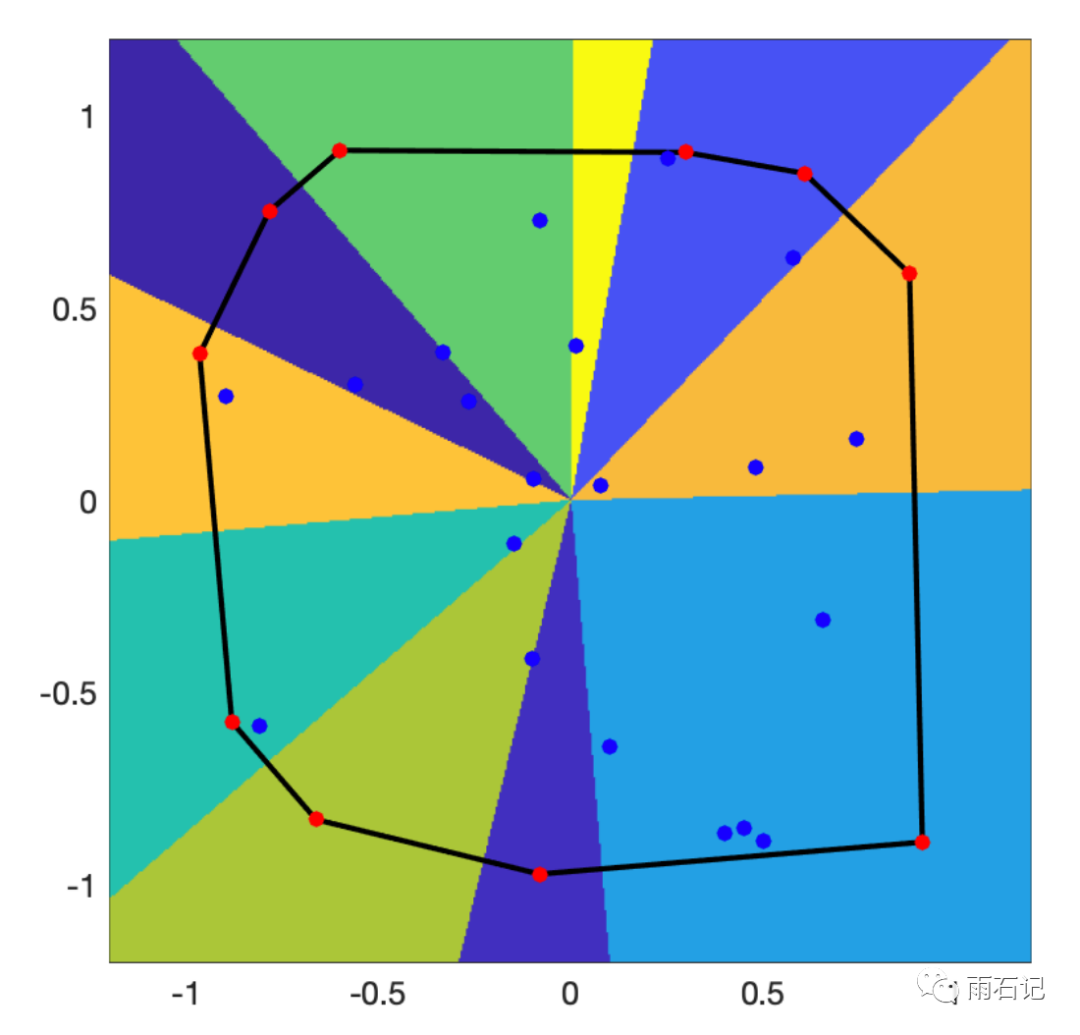
这就使我们得到一个很有意思的图：

这张图是内积的沃罗诺伊块。它跟上面的基于-||x-y||的沃罗诺伊块有这么几个区别：

蓝色的点是没有沃罗诺伊块的，因为对于任意的q，总会有一个点和q的内积比蓝色点要大。
红色的点是有沃罗诺伊块的，这些点又被称为极点，因为对于任意的q，一定和某个红色点的内积是最大的。
这些红色的点，组成了一个凸包。

本部分内容来源于参考文献[1].

莫比乌斯变换——连接l2-Delaunay和ip-Delaunay的桥梁

ip-Delaunay图虽然可行，但是却有一些缺点，那就是很多在l2-Delaunay上能够应用的技巧都不怎么起效，比如：

在层次德劳内图上可以使用的选边技巧都不能使用
层次德劳内图在ANN上可以起效，但是在MIPS上收效甚微。

听起来还是要使用l2-Delaunay才可以，但是该怎么应用呢？

这就要靠一个神奇的变换——莫比乌斯变换。

莫比乌斯变换不是一个变换，而是一组变换。

在这里，使用的莫比乌斯变换是y = x / ||x||^2，即每个向量除以自己的平方。大家注意到这里的这个||x||^2其实是x这个点距离原点的距离的平方，所以在变换后点到原点的距离变成1/||x||。因而原来距离远点越远的点，在经过这个变换后就越近。

然后，大家在上一部分的内积的沃罗诺伊块的图上，会发现，ip-Delaunay上所使用的点是距离原点比较远的那一批，因而，在经过这个变换后，这些点都变成了距离原点比较近的那一批。

因而，这个时候，我们在变换后的数据上加入原点，然后构建好l2-Delaunay后，那么原点的所有neighbors就是ip-Delaunay上的点，它们是同构的。

论文[5]花费了大量的篇幅来从数学的角度证明这个同构性，但是因为我数学基础有限，已经无法解释，撞到了我自己的智子墙壁。后悔大学没有学二学位。

所以构建德劳内图的方法就变成：

需要注意的是，在使用变换后的数据构建了l2-Delaunay图后，保持这个结构，记录下来原点的所有邻居节点集合N，然后移除原点，再用对应的原数据替换这些变换后的数据点。而在搜索的时候，就从集合N出发，用一种类似beam search的算法去进行BFS。

然后，其他的算法部分伪代码如下：

本部分主要来源于参考论文[5]。

回到ip-Delaunay

莫比乌斯转换算是一种曲线救国之策，那么，有没有可能继续从纯种的ip-Delaunay上考虑呢？

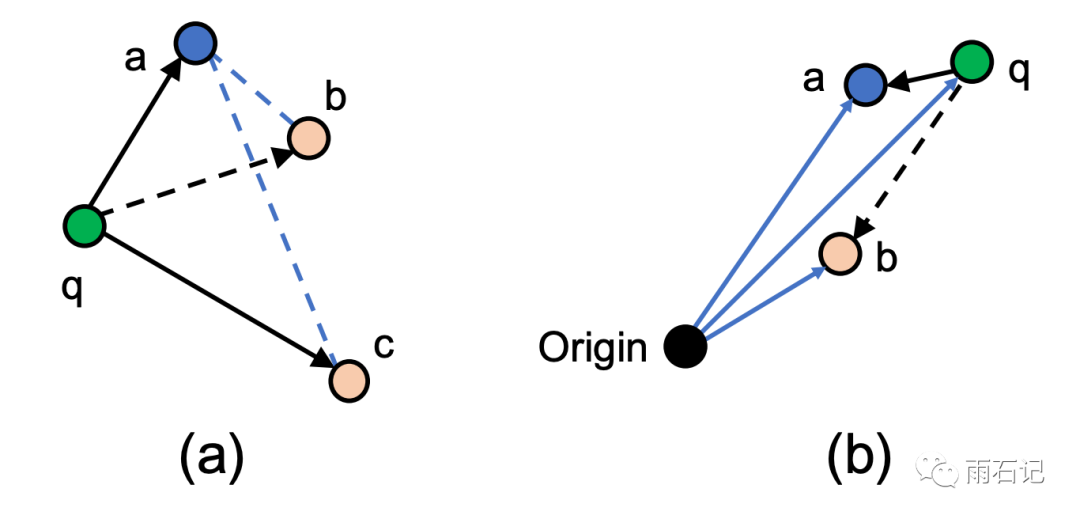
答案是有的，之前的l2-Delaunay上的策略不好用，那么把策略改掉不就可以了？如下图：

在l2-Delaunay中，为了保证点的多样性，假设a是已经在图中的点，那么对于q点来说，首先q->a边已经添加，那么在考虑b和c的时候，因为dis(q, b) < dis(a, b)，所以认为b需要被a连接而不是被q，所以q->b这条边不应该添加。同理，q->c需要被添加。这是在l2空间上的策略。

但是在ip-Delaunay中，这样的策略就不适用。因为，虽然dis(q, b) > dis(a, b)，但是对于大部分的q'来说，dis(q', a) > dis(q', b),意味着b这个点可有可无，因而需要判断的条件是dis(b, b) > dis(a, b)。

这部分的伪代码如下17-28行：

另外一个可以改进的地方是极点，因为极点是ip-Delaunay的骨干和精髓，所以极点上的边应该多一些，但是使用贪心策略构建德劳内图的时候，边多的点不是极点而是先加入的点。这就会导致变差了。所以提出了一种循环更新法，即在构建好Delaunay图之后，对于每个点，再重新更新一遍邻居节点。

搜索算法如下：

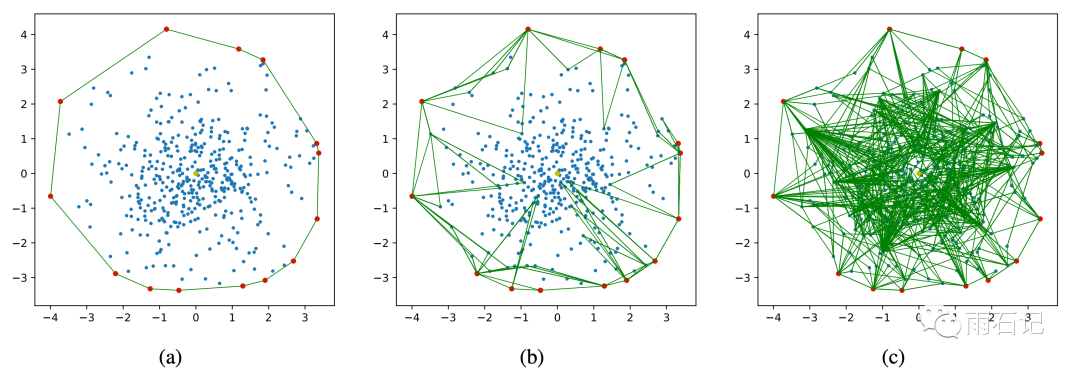
使用了上面两种方法后，构建的ip-Delaunay非常接近理想状态，如下图：

左图是理想状态，中图是改进后算法，右图是原来的贪心算法构建的图。

本部分内容主要来自于参考文献[4]。

总结

本文为大家详细解释了最大内积搜索算法中的基于图的解决方法，也是现在海量数据上非常行之有效的向量查询算法。

其中，给大家讲述了两个概念，德劳内图和沃罗诺伊块。以及基于它们是怎么去做最近邻搜索的。然后解释了最近邻搜索和内积搜索的区别和联系。然后介绍了内积搜索的几种优化方法，包括层次化Delaunay，莫比乌斯变换，策略更新等。

这种基于图的方式相比与基于哈希的方式，损失更小，可解释性更强。

新学之知识，难免有疏漏，望大家不吝赐教。

参考文献

Morozov S, Babenko A. Non-metric similarity graphs for maximum inner product search[C]//Advances in Neural Information Processing Systems. 2018: 4721-4730.
Malkov Y, Ponomarenko A, Logvinov A, et al. Approximate nearest neighbor algorithm based on navigable small world graphs[J]. Information Systems, 2014, 45: 61-68.
Malkov Y A, Yashunin D A. Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs[J]. IEEE transactions on pattern analysis and machine intelligence, 2018.
Tan S, Zhou Z, Xu Z, et al. On efficient retrieval of top similarity vectors[C]//Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). 2019: 5239-5249.
Zhou Z, Tan S, Xu Z, et al. Möbius Transformation for Fast Inner Product Search on Graph[C]//Advances in Neural Information Processing Systems. 2019: 8216-8227.

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方"AINLP"，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。