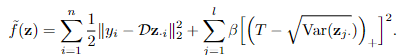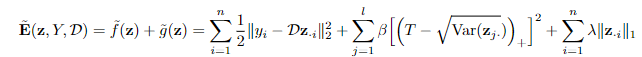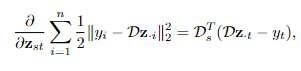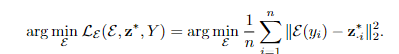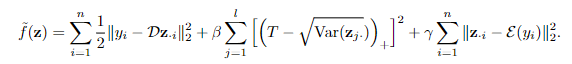LeCun新作，一张卡就能训！方差正则，抛弃L1正则，稀疏编码器不再崩溃

---

  新智元报道  

编辑：LRS

【新智元导读】最近LeCun又发新作，依然是崩溃问题，依然是自监督，这次提出了一个新的正则化方法：方差正则，可以有效防止编码崩溃，还能提升重构质量，一张显卡就能训！

神经网络中有一类学习特别受研究人员的青睐，那就是自监督学习（self-supervised learning SSL）。

 

 

只要给足够多的数据，自监督学习能够在完全不需要人工标注的情况下，学习到文本、图像的表征，并且数据量越大、模型参数量越大，效果越好。

 

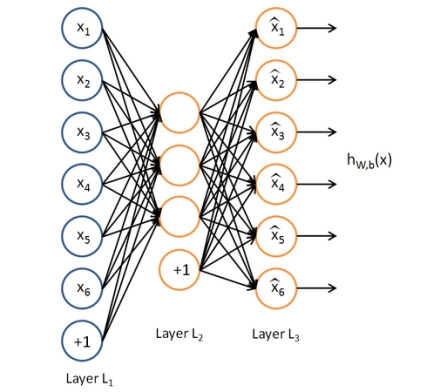
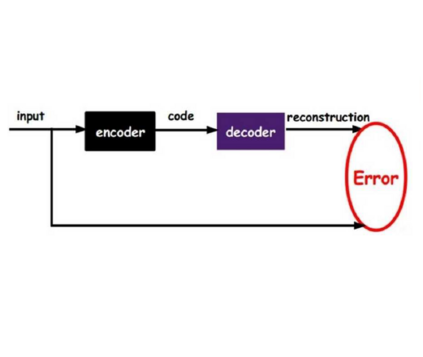
自监督学习的工作原理也很简单：例如应用场景是图片的话，我们可以把SSL模型的输入和输出都设置为同一张图片，中间加入一个隐藏层，然后开训！

 

一个最简单的自编码器AutoEncoder就弄好了。

 

 

通常来说隐藏层的神经元数量是要小于输入图片的，这样训练后，自编码器的中间隐藏层就可以作为图片的表征向量，因为训练过程的目标就是仅用该隐藏向量即可还原图片。

 

自编码器最初提出是基于降维的思想，但是当隐层节点比输入节点多时，自编码器就会失去自动学习样本特征的能力，此时就需要对隐藏层节点进行一定的约束。

 

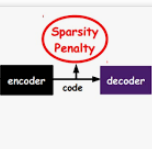
稀疏自编码器应运而生，约束的出发点来自于：高维而稀疏的表达是好的。所以只需要对隐藏层节点进行稀疏性约束即可。

 

常用的稀疏编码方式当然是L1正则。

 

最近LeCun提出了一种新的稀疏编码协议可以防止编码的崩溃，而不需要对解码器进行正则化处理。新的编码协议直接对编码进行正则化，使每个潜码成分（latent code component）在一组给定的输入的稀疏表示上具有大于固定阈值的方差。

 

论文：https://arxiv.org/abs/2112.09214

开源代码：https://github.com/kevtimova/deep-sparse

 

此外，研究人员还探索了如何利用多层解码器来有效训练稀疏编码系统的方法，可以比线性字典（linear dictionary）模拟更复杂的关系。

 

在对MNIST和自然图像块（natural image patch）的实验中，实验结果表明使用新方法学习到的解码器在线性和多层情况下都有可解释的特征。

 

与使用线性字典的自动编码器相比，使用方差正则化方法训练的具有多层解码器的稀疏自动编码器可以产生更高质量的重建，也表明方差正则化方法得到的稀疏表征在低数据量下的去噪和分类等下游任务中很有用。

 

论文中LeCun的作者单位也是从FAIR更名为Meta AI Research（MAIR）。

 

方差正则

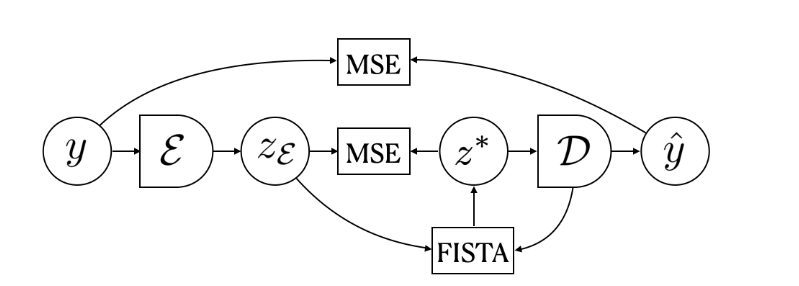
给定一个输入y和一个固定的解码器D，研究人员使用FISTA算法（近似梯度方法ISTA的快速版）进行推理来找到一个稀疏编码z*，得到的z*可以使用D中的元素最好地重建输入y。

 

解码器D的权重是通过最小化输入y和从z∗计算出的重构y之间的平均平方误差（MSE）来训练得到的。

 

编码器E的权重则是通过预测FISTA的输出z∗得到。

 

 

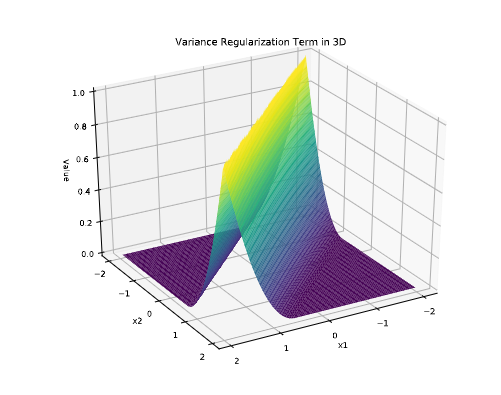
为了防止潜码的L1正则崩溃，研究人员加入了一个限制条件，确保每个潜码方差大于预先设定的阈值。主要实现方法就是对能量函数加入一个正则化项，从而能够促使所有潜码分量的方差保持在预设的阈值以上。

 

 

更具体地说，研究人员修改了推理过程中的目标函数来最小化能量。

 

 

其中hinge项与L1惩罚项相抵消作为新的正则化项，新的方程可以鼓励每个潜伏代码成分的方差保持在的阈值以上，从而可以防止潜码的L1正则崩溃，进而无需对解码器权重进行正则化。

 

重构项求和之后的梯度和潜码z对应。

 

 

对于线性解码器来说，尽管hinge项不是光滑的凸函数，但梯度是一条线（line）意味着hinge项在局部表现得像一个凸二次函数。

 

 

训练过程中，研究人员将编码器E与解码器D同时训练来预测FISTA推理计算的稀疏编码。

 

同时训练的第一个原因是为了避免在解码器训练完成后使用批量统计来计算编码。事实上，应该可以为不同的输入独立地计算编码。

 

第二个原因是为了减少推理时间。编码器和解码器的训练完成后，编码器可以直接计算输入的稀疏表示，这样就不需要用FISTA进行推理，即编码器可以进行amoritized推理。

 

 

编码器的正则项可以促使FISTA找到可以被编码器学习到的编码。在实验设置中，编码器的预测通常被视为常数（constants），用作FIST编码的初始值。

 

 

如果编码器提供了一个好的初始值，则可以通过减少FISTA迭代的次数来减少推理时间。

 

实验设置

实验中的编码器为一个LISTA（Learned ISTA）编码器，它的设计是为了模仿ISTA推理的输出，类似于一个递归神经网络。编码器由两个全连接层，一个偏置项，以及ReLU激活函数组成。

 

 

线性解码器的参数简单地说是一个线性变换，将编码映射到输入数据的重构维度上，在线性变换中没有偏置项。

 

在非线性解码器的情况下，使用一个大小为m的隐藏层和大小为l的输入层（潜码的size）的全连接网络，使用ReLU作为隐藏层的激活函数。将输入代码映射到隐含表征的层中有一个偏置项，而将隐含表征映射到输出的层没有偏置项。

 

在推理过程中，编码z被限制为非负值。MNIST实验中潜码的维度为128，在ImageNet patch的实验中则是256，当batch size为250时，对于VDL中每个潜成分（latent component）的方差的正则化项来说是足够大的。

 

将FISTA的最大迭代次数K设置为200次，已经足以实现一个效果不错的重构模型了。

 

在自编码器训练中，研究人员设置MNIST的epoch为200，image patch则为100。在SDL和SDL-NL实验中，将解码器的全连接层W、W1和W2中的列的L2正则固定为1，并保存输出平均能量最低的自编码器。

 

研究人员还对SDL-NL和VDL-NL模型中的偏置项b1以及LISTA编码器中的偏置项b增加了权重衰减，以防止其正则化项无限膨胀。

 

模型的训练只需要一块NVIDIA RTX 8000 GPU卡，并且所有实验的运行时间都在24小时以内。

 

实验结果可以看到，对于两个SDL和两个VDL的字典元素（dictionary elements）来说，在稀疏度λ较低的情况下（0.001， 0.005）解码器似乎可以学到方向、笔划，甚至是是数字图形中的一部分。

 

随着λ值的提高，生成的图像也越来越像一个完整的数字，完成了从笔划到数字的演化。

 

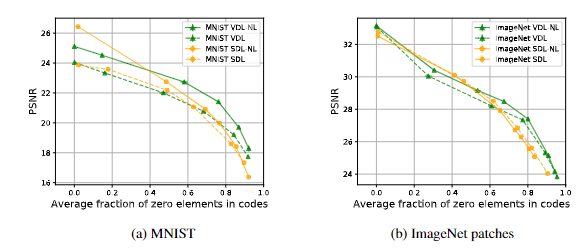
在重构质量上，SDL和VDL模型的编码器的曲线显示了由未激活编码（值为0）成分的平均百分比衡量的稀疏程度和由平均PSNR衡量的重建质量之间的权衡。

 

 

在5个随机种子上的测试集所衡量的重建质量和预期相符，较高的稀疏度会导致更差的重建效果，但用文中提出的方差正则化方法训练出来的模型则会比SDL 模型在更高的稀疏程度下产生更好的重建效果，从而证实了方差正则化确实是有效的。

参考资料：

https://arxiv.org/abs/2112.09214