Mimetic finite difference schemes for transport operators with divergence-free advective field and applications to plasma physics

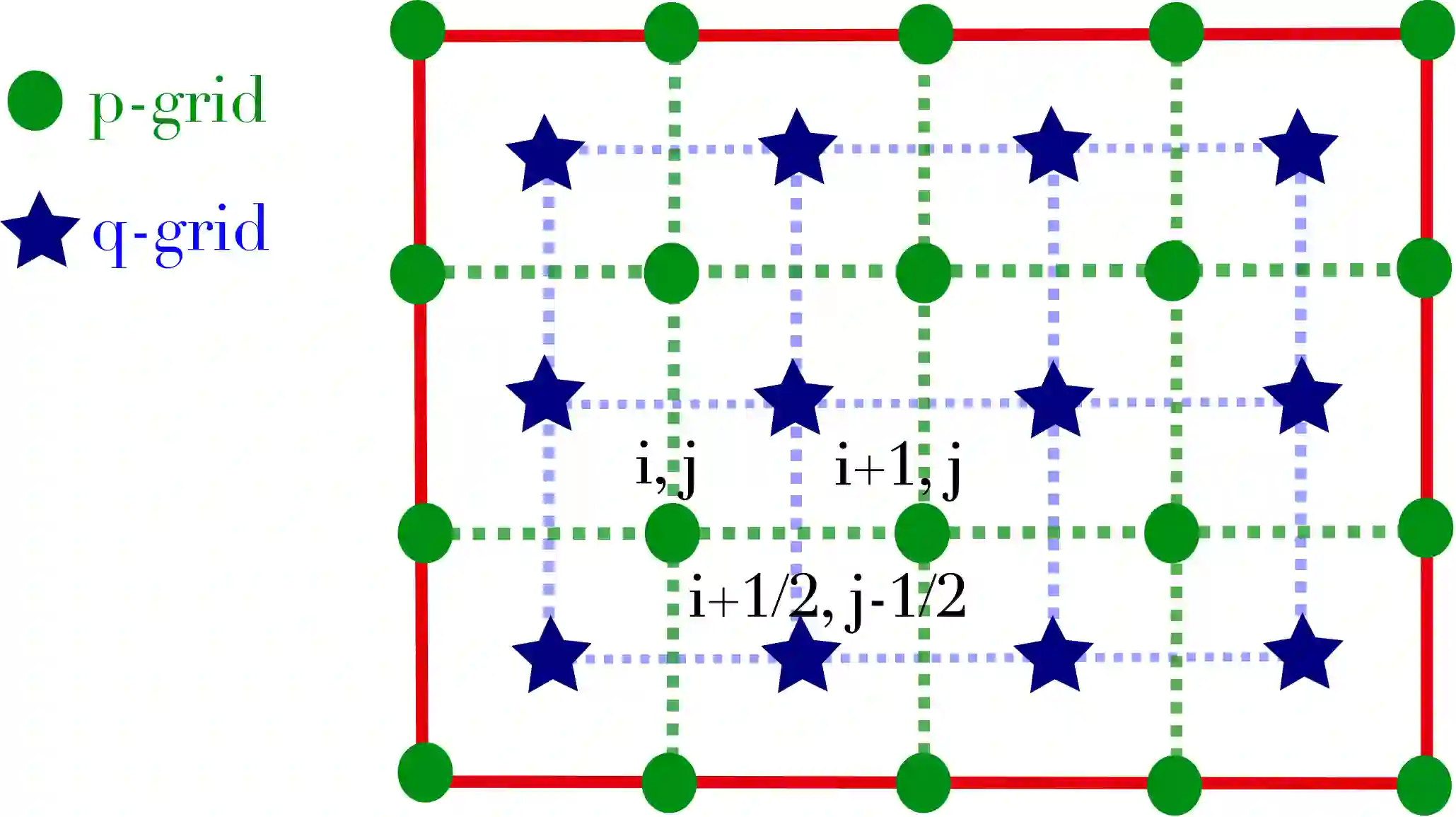
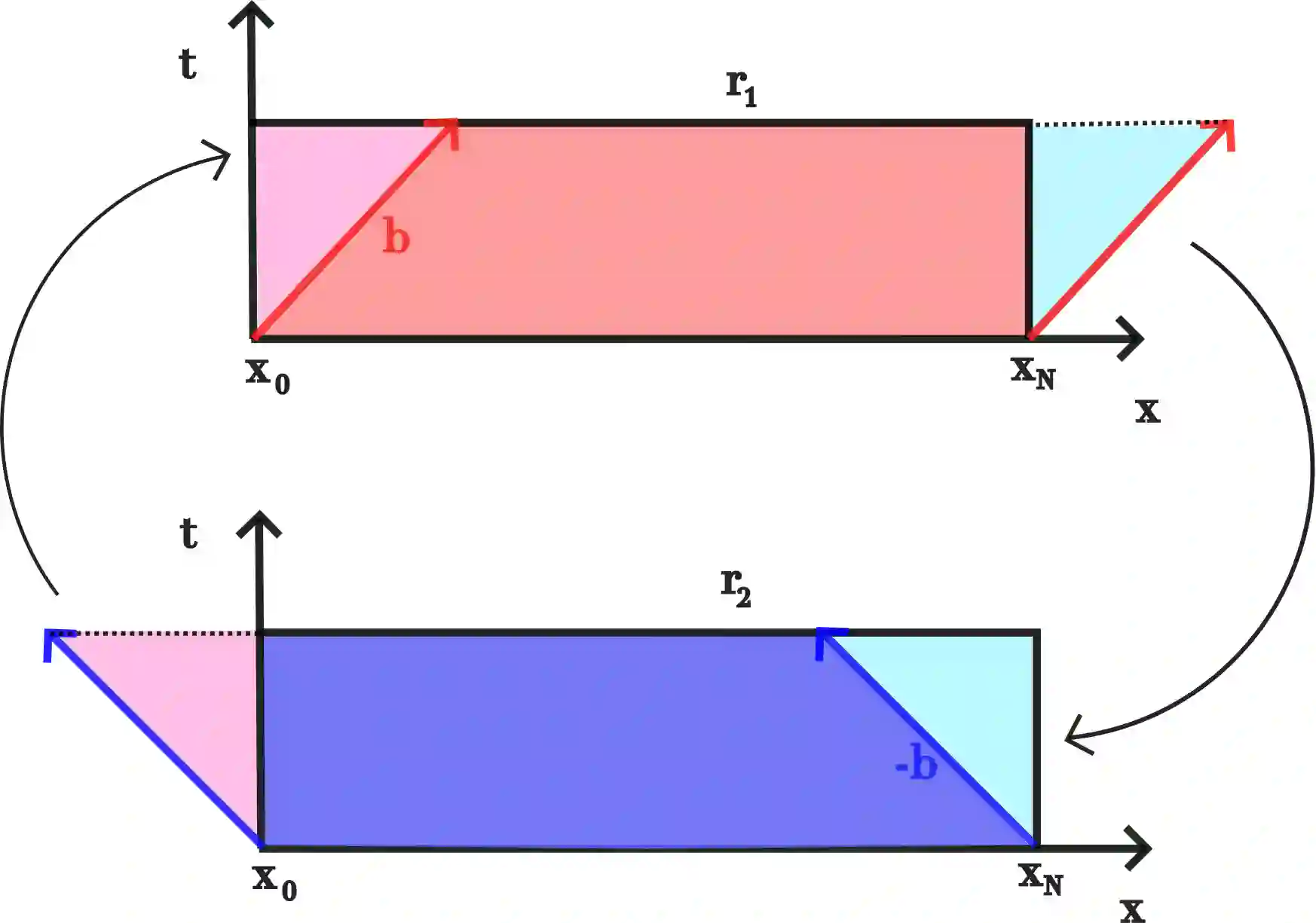
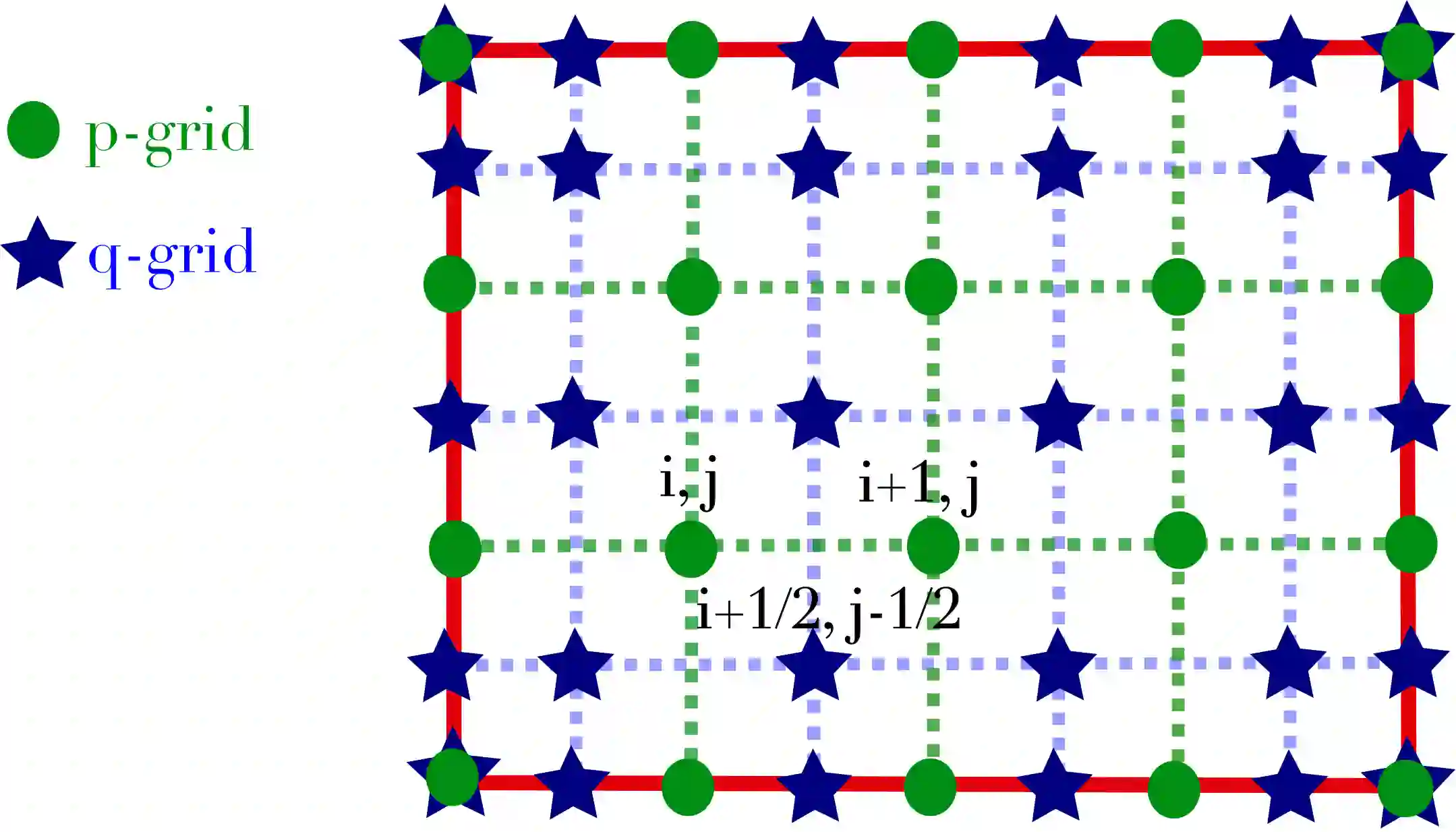
In wave propagation problems, finite difference methods implemented on staggered grids are commonly used to avoid checkerboard patterns and to improve accuracy in the approximation of short-wavelength components of the solutions. In this study, we develop a mimetic finite difference (MFD) method on staggered grids for transport operators with divergence-free advective field that is proven to be energy-preserving in wave problems. This method mimics some characteristics of the summation-by-parts (SBP) operators framework, in particular it preserves the divergence theorem at the discrete level. Its design is intended to be versatile and applicable to wave problems characterized by a divergence-free velocity. As an application, we consider the electrostatic shear Alfv\'en waves (SAWs), appearing in the modeling of plasmas. These waves are solved in a magnetic field configuration recalling that of a tokamak device. The study of the generalized eigenvalue problem associated with the SAWs shows the energy conservation of the discretization scheme, demonstrating the stability of the numerical solution.