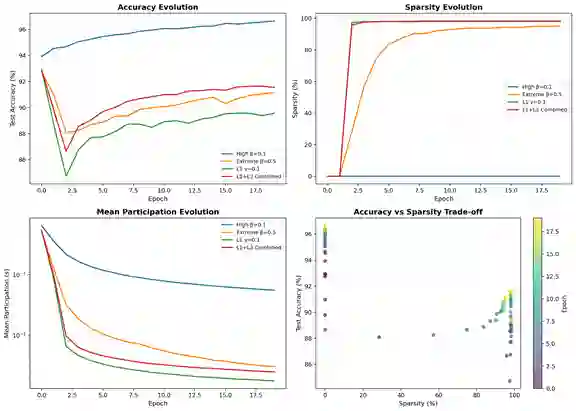
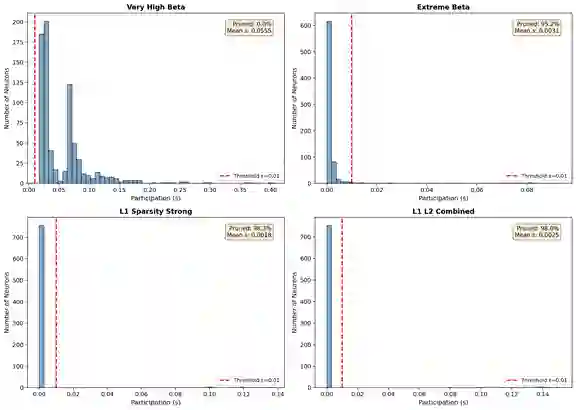
Neural network pruning is widely used to reduce model size and computational cost. Yet, most existing methods treat sparsity as an externally imposed constraint, enforced through heuristic importance scores or training-time regularization. In this work, we propose a fundamentally different perspective: pruning as an equilibrium outcome of strategic interaction among model components. We model parameter groups such as weights, neurons, or filters as players in a continuous non-cooperative game, where each player selects its level of participation in the network to balance contribution against redundancy and competition. Within this formulation, sparsity emerges naturally when continued participation becomes a dominated strategy at equilibrium. We analyze the resulting game and show that dominated players collapse to zero participation under mild conditions, providing a principled explanation for pruning behavior. Building on this insight, we derive a simple equilibrium-driven pruning algorithm that jointly updates network parameters and participation variables without relying on explicit importance scores. This work focuses on establishing a principled formulation and empirical validation of pruning as an equilibrium phenomenon, rather than exhaustive architectural or large-scale benchmarking. Experiments on standard benchmarks demonstrate that the proposed approach achieves competitive sparsity-accuracy trade-offs while offering an interpretable, theory-grounded alternative to existing pruning methods.
翻译:神经网络剪枝被广泛用于减小模型规模与计算开销。然而,现有方法大多将稀疏性视为外部施加的约束,通过启发式重要性评分或训练时正则化来强制执行。本文提出一种根本不同的视角:将剪枝视为模型组件间策略交互的均衡结果。我们将权重、神经元或滤波器等参数组建模为连续非合作博弈中的参与者,每个参与者选择其在网络中的参与程度,以平衡自身贡献与冗余及竞争之间的关系。在此框架下,当持续参与在均衡状态下成为被占优策略时,稀疏性便自然涌现。我们分析了所构建的博弈模型,证明在温和条件下被占优的参与者会退化为零参与,从而为剪枝行为提供了理论解释。基于这一洞见,我们推导出一种简单的均衡驱动剪枝算法,该算法联合更新网络参数与参与变量,无需依赖显式的重要性评分。本文重点在于建立剪枝作为均衡现象的理论框架并进行实证验证,而非进行详尽的架构探索或大规模基准测试。在标准基准上的实验表明,所提方法在实现具有竞争力的稀疏性-准确性权衡的同时,为现有剪枝方法提供了一种可解释且理论依据充分的替代方案。