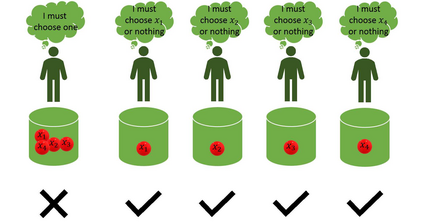
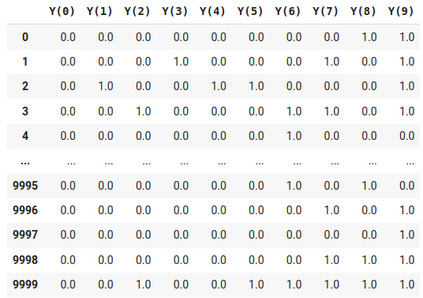
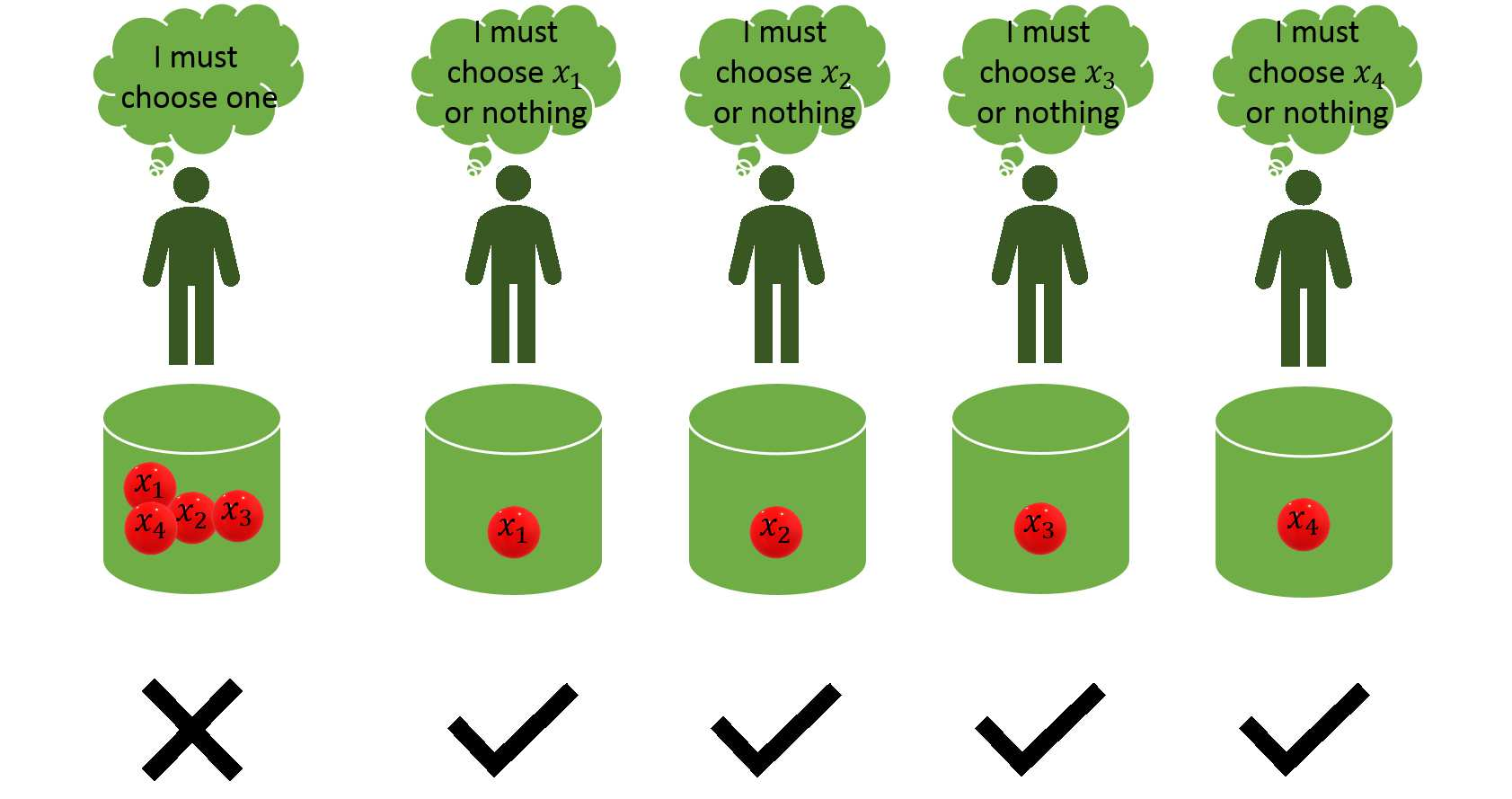
In this paper, we introduce a fundamental framework to create a bridge between Probability Theory and Fuzzy Logic. Indeed, our theory formulates a random experiment of selecting crisp elements with the criterion of having a certain fuzzy attribute. To do so, we associate some specific crisp random variables to the random experiment. Then, several formulas are presented, which make it easier to compute different conditional probabilities and expected values of these random variables. Also, we provide measure theoretical basis for our probabilistic fuzzy logic framework. Note that in our theory, the probability density functions of continuous distributions which come from the aforementioned random variables include the Dirac delta function as a term. Further, we introduce an application of our theory in Causal Inference.
翻译:在本文中,我们引入了一个在概率理论和模糊逻辑逻辑之间搭桥的基本框架。 事实上, 我们的理论将选择精密元素的随机实验与具有某种模糊属性的标准相提并论。 为此, 我们将某些具体的精密随机变量与随机实验联系起来。 然后, 我们提出几种公式, 从而更容易计算这些随机变量不同的有条件概率和预期值。 此外, 我们还为我们概率模糊逻辑框架提供了测量理论基础。 注意在我们的理论中, 来自上述随机变量的连续分布的概率密度函数包括Dirac delta 函数作为一个术语。 此外, 我们还在Causal Inference 中引入了我们理论的应用。