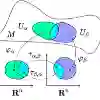
Being infinite dimensional, non-parametric information geometry has long faced an "intractability barrier" due to the fact that the Fisher-Rao metric is now a functional incurring difficulties in defining its inverse. This paper introduces a novel framework to resolve the intractability with an Orthogonal Decomposition of the Tangent Space ($T_fM=S \oplus S^{\perp}$), where S represents an observable covariate subspace. Through the decomposition, we derive the Covariate Fisher Information Matrix (cFIM), denoted as $G_f$, which is a finite-dimensional and computable representative of information extractable from the manifold's geometry. Indeed, by proving the Trace Theorem: $H_G(f)=\text{Tr}(G_f)$, we establish a rigorous foundation for the G-entropy previously introduced by us, thereby identifying it not merely as a gradient-based regularizer, but also as a fundamental geometric invariant representing the total explainable statistical information captured by the probability distribution associated with the model. Furthermore, we establish a link between $G_f$ and the second-order derivative (i.e. the curvature) of the KL-divergence, leading to the notion of Covariate Cramér-Rao Lower Bound(CRLB). We demonstrate that $G_f$ is congruent to the Efficient Fisher Information Matrix, thereby providing fundamental limits of variance for semi-parametric estimators. Finally, we apply our geometric framework to the Manifold Hypothesis, lifting the latter from a heuristic assumption into a testable condition of rank-deficiency within the cFIM. By defining the Information Capture Ratio, we provide a rigorous method for estimating intrinsic dimensionality in high-dimensional data. In short, our work bridges the gap between abstract information geometry and the demand of explainable AI, by providing a tractable path for revealing the statistical coverage and the efficiency of non-parametric models.
翻译:无限维非参数信息几何长期面临"难处理性壁垒",其根源在于Fisher-Rao度量现为泛函,导致其逆的定义存在困难。本文提出一种创新框架,通过切空间的正交分解($T_fM=S \oplus S^{\perp}$)解决该难题,其中S表示可观测协变量子空间。通过该分解,我们推导出协变量Fisher信息矩阵(cFIM),记为$G_f$,它是从流形几何中可提取信息的有限维可计算表示。事实上,通过证明迹定理:$H_G(f)=\text{Tr}(G_f)$,我们为先前提出的G-熵建立了严格理论基础,从而将其不仅识别为基于梯度的正则化项,更确认为表征模型相关概率分布所捕获可解释统计信息总量的基本几何不变量。此外,我们建立了$G_f$与KL散度二阶导数(即曲率)的关联,由此引出协变量Cramér-Rao下界(CRLB)的概念。我们证明$G_f$与有效Fisher信息矩阵合同,从而为半参数估计量提供了方差的基本下界。最后,我们将该几何框架应用于流形假设,将后者从启发式假设提升为cFIM内秩亏缺的可检验条件。通过定义信息捕获比,我们为高维数据本征维度的估计提供了严格方法。简言之,本研究通过开辟揭示非参数模型统计覆盖范围与效率的可处理路径,弥合了抽象信息几何与可解释AI需求之间的鸿沟。