Efficient Data Structures for Exploiting Sparsity and Structure in Representation of Polynomial Optimization Problems: Implementation in SOSTOOLS

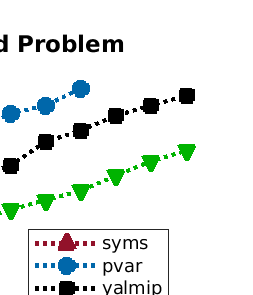
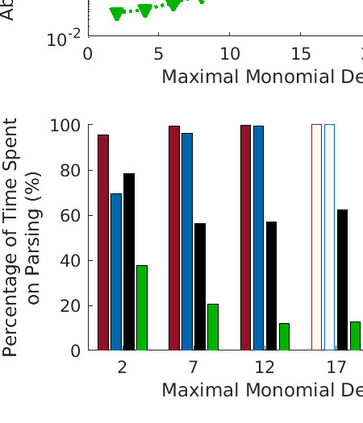
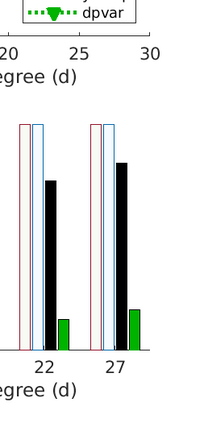
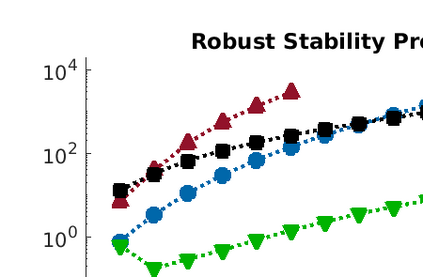
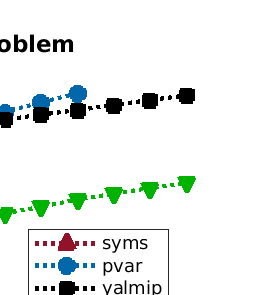
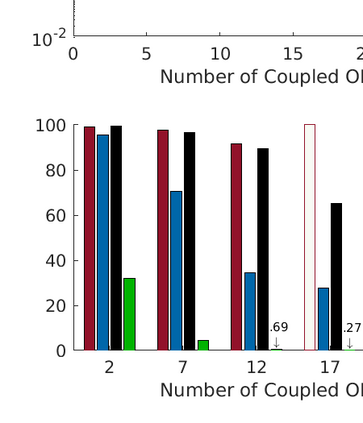
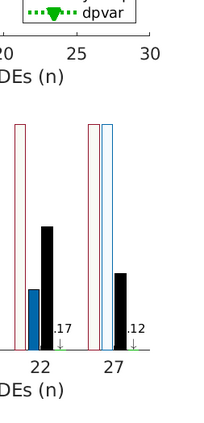
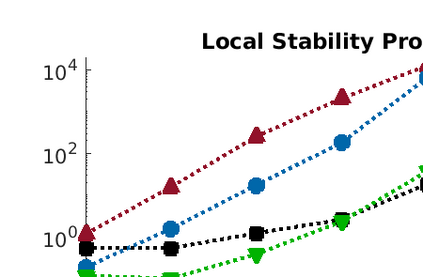
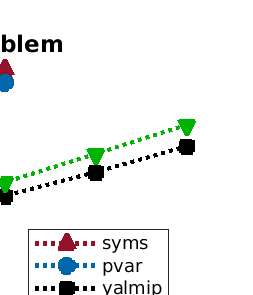
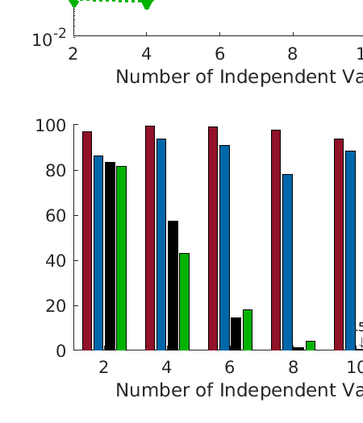
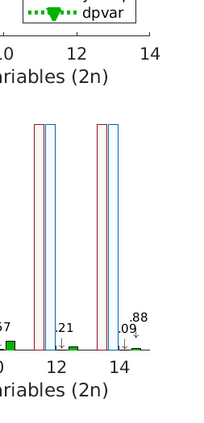
We present a new data structure for representation of polynomial variables in the parsing of sum-of-squares (SOS) programs. In SOS programs, the variables $s(x;P)$ are polynomial in the independent variables $x$, but linear in the decision variables $P$. Current SOS parsers, however, fail to exploit the semi-linear structure of the polynomial variables, treating the decision variables as independent variables in their representation. This results in unnecessary overhead in storage and manipulation of the polynomial variables, prohibiting the parser from addressing larger-scale optimization problems. To eliminate this computational overhead, we introduce a new representation of polynomial variables, the "dpvar" structure, that is affine in the decision variables. We show that the complexity of operations on variables in the dpvar representation scales favorably with the number of decision variables. We further show that the required memory for storing polynomial variables is relatively small using the dpvar structure, particularly when exploiting the MATLAB sparse storage structure. Finally, we incorporate the dpvar data structure into SOSTOOLS 4.00, and test the performance of the parser for several polynomial optimization problems.