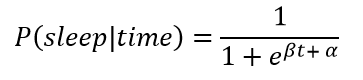用Python入门不明觉厉的马尔可夫链蒙特卡罗（附案例代码）

大数据文摘作品

编译：Niki、张南星、Shan LIU、Aileen

这篇文章让小白也能读懂什么是人们常说的Markov Chain Monte Carlo。

在过去几个月里，我在数据科学的世界里反复遇到一个词：马尔可夫链蒙特卡洛（Markov Chain Monte Carlo , MCMC）。在我的研究室、podcast和文章里，每每遇到这个词我都会“不明觉厉”地点点头，觉得这个算法听起来很酷，但每次听人提起也只是有个模模糊糊的概念。

我屡次尝试学习MCMC和贝叶斯推论，而一拿起书，又很快就放弃了。无奈之下，我选择了学习任何新东西最佳的方法：应用到一个实际问题中。

通过使用一些我曾试图分析的睡眠数据和一本实操类的、基于应用教学的书（《写给开发者的贝叶斯方法》，我最终通过一个实际项目搞明白了MCMC。

《写给开发者的贝叶斯方法》

https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers

和学习其他东西一样，当我把这些技术性的概念应用于一个实际问题中而不是单纯地通过看书去了解这些抽象概念，我更容易理解这些知识，并且更享受学习的过程。

这篇文章介绍了马尔可夫链蒙特卡洛在Python中入门级的应用操作，这个实际应用最终也使我学会使用这个强大的建模分析工具。

此项目全部的代码和数据：

https://github.com/WillKoehrsen/ai-projects/blob/master/bayesian/bayesian_inference.ipynb

这篇文章侧重于应用和结果，因此很多知识点只会粗浅的介绍，但对于那些想了解更多知识的读者，在文章也尝试提供了一些学习链接。

案例简介

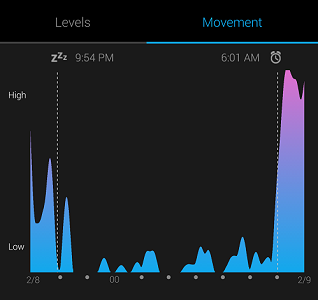
我的智能手环在我入睡和起床时会根据心率和运动进行记录。它不是100%准确的，但现实世界中的数据永远不可能是完美的，不过我们依然可以运用正确的模型从这些噪声数据提取出有价值的信息。

典型睡眠数据

这个项目的目的在于运用睡眠数据建立一个能够确立睡眠相对于时间的后验分布模型。由于时间是个连续变量，我们无法知道后验分布的具体表达式，因此我们转向能够近似后验分布的算法，比如马尔可夫链蒙特卡洛（MCMC）。

选择一个概率分布

在我们开始MCMC之前，我们需要为睡眠的后验分布模型选择一个合适的函数。一种简单的做法是观察数据所呈现的图像。下图呈现了当我入睡时时间函数的数据分布。

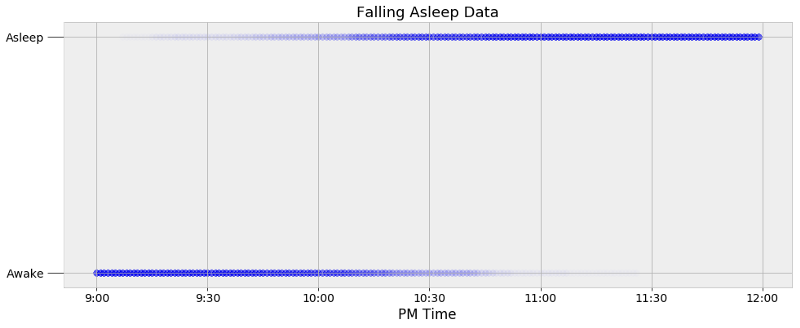
睡眠数据

每个数据点用一个点来表示，点的密度展现了在固定时刻的观测个数。我的智能手表只记录我入睡的那个时刻，因此为了扩展数据，我在每分钟的两端添加了数据点。如果我的手表记录我在晚上10：05入睡，那么所有在此之前的时间点被记为0（醒着），所有在此之后的时间点记为1（睡着）。这样一来，原本大约60夜的观察量被扩展成11340个数据点。

可以看到我趋向于在10：00后几分钟入睡，但我们希望建立一个把从醒到入睡的转变用概率进行表达的模型。我们可以用一个简单的阶梯函数作为模型，在一个精确时间点从醒着（0）变到入睡（1），但这不能代表数据中的不确定性。

我不会每天在同一时间入睡，因此我们需要一个能够模拟出这个个渐变过程的函数来展现变化当中的差异性。在现有数据下最好的选择是logistic函数，在0到1之前平滑地移动。下面这个公式是睡眠状态相对时间的概率分布，也是一个logistic公式。

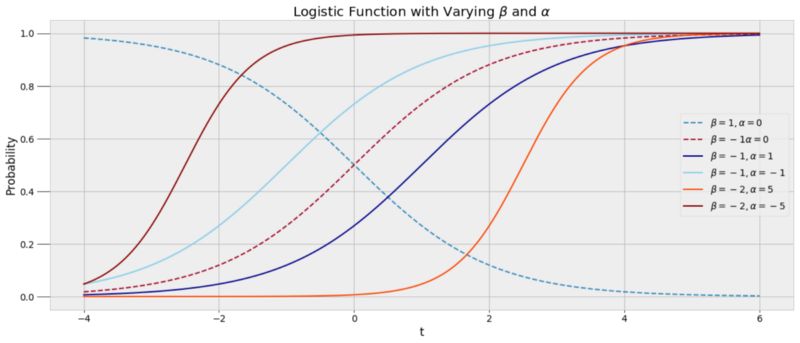
在这里，β (beta) 和 α (alpha) 是模型的参数，我们只能通过MCMC去模拟它们的值。下面展示了一个参数变化的logistic函数。

一个logistic函数能够很好的拟合数据，因为在logistic函数中入睡的概率在逐渐改变，捕捉了我睡眠模式的变化性。我们希望能够带入一个具体的时间t到函数中，从而得到一个在0到1之间的睡眠状态的概率分布。我们并不会直接得到我是否在10：00睡着了的准确答案，而是一个概率。创建这个模型，我们通过数据和马尔可夫链蒙特卡洛去寻找最优的alpha和beta系数估计。

马尔可夫链蒙特卡洛

马尔可夫链蒙特卡罗是一组从概率分布中抽样，从而建立最近似原分布的函数的方法。因为我们不能直接去计算logistic分布，所以我们为系数(alpha 和 beta)生成成千上万的数值-被称为样本-去建立分布的一个模拟。MCMC背后的基本思想就是当我们生成越多的样本，我们的模拟就更近似于真实的分布。

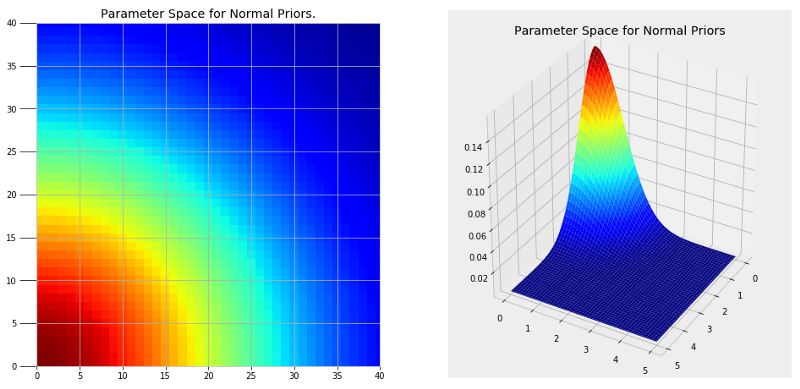
马尔可夫链蒙特卡洛由两部分组成。蒙特卡洛代表运用重复随机的样本来获取一个准确答案的一种模拟方法。蒙特卡洛可以被看做大量重复性的实验，每次更改变量的值并观察结果。通过选择随机的数值，我们可以在系数的范围空间，也就是变量可取值的范围，更大比例地探索。下图展示了在我们的问题中，一个使用高斯分布作为先验的系数空间。

能够清楚地看到我们不能在这些图中一一找出单个的点，但通过在更高概率的区域（红色）进行随机抽样，我们就能够建立最近似的模型。

马尔可夫链（Markov Chain）

马尔可夫链是一个“下个状态值只取决于当前状态”的过程。（在这里，一个状态指代当前时间系数的数值分配）。一个马尔可夫链是“健忘”的，因为如何到达当前状态并不要紧，只有当前的状态值是关键。如果这有些难以理解的话，让我们来设想一个每天都会经历的情景--天气。

如果我们希望预测明天的天气，那么仅仅使用今天的天气状况我们就能够得到一个较为合理的预测。如果今天下雪，我们可以观测有关下雪后第二天天气的历史数据去预测明天各种天气状况的可能性。马尔可夫链的定义就是我们不需要知道一个过程中的全部历史状态去预测下一节点的状态，这种近似在许多现实问题中都很有用。

把马尔可夫链（Markov Chain）和蒙特卡洛（Monte Carlo），两者放到一起，就有了MCMC。MCMC是一种基于当前值，重复为概率分布系数抽取随机数值的方法。每个样本都是随机的，但是数值的选择也受当前值和系数先验分布的影响。MCMC可以被看做是一个最终趋于真实分布的随机游走。

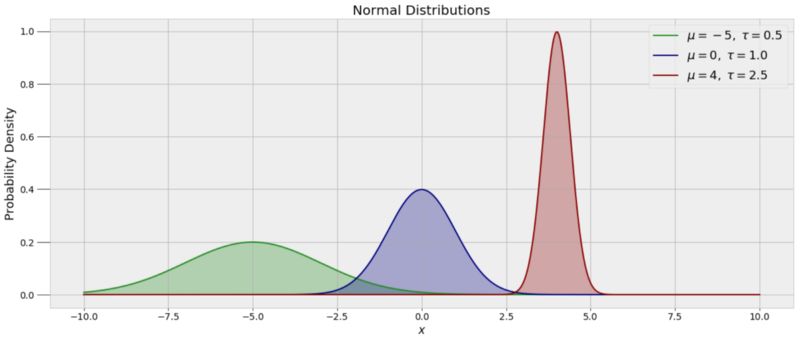
为了能够抽取alpha 和 beta的随机值，我们需要为每个系数假设一个先验分布。因为我们没有对于这两个系数的任何假设，我们可以使用正太分布作为先验。正太分布，也称高斯分布，是由均值（展示数据分布），和方差（展示离散性）来定义的。下图展示了多个不同均值和离散型的正态分布。

具体的MCMC算法被称作Metropolis Hastings。为了连接我们的观察数据到模型中，每次一组随机值被抽取，算法将把它们与数据进行比较。一旦它们与数据不吻合（在这里我简化了一部分内容），这些值就会被舍弃，模型将停留在当前的状态值。

如果这些随机值与数据吻合，那么这些值就被接纳为各个系数新的值，成为当前的状态值。这个过程会有一个提前设置好的迭代次数，次数越多，模型的精确度也就越高。

把上面介绍的整合到一起，就能得到在我们的问题中所需进行的最基本的MCMC步骤：

• 为logistic函数的系数alpha 和beta选择初始值。

  
  

• 基于当前状态值随机分配给alpha 和beta新的值。

  
  

• 检查新的随机值是否与观察数据吻合。如果不是，舍弃掉这个值，并回到上一状态值。如果吻合，接受这个新的值作为当前状态值。

  
  

• 重复步骤2和3（重复次数提前设置好）。

  
  

• 这个算法会给出所有它所生成的alpha 和beta值。我们可以用这些值的平均数作为alpha 和beta在logistic函数中可能性最大的终值。MCMC不会返回“真实”的数值，而是函数分布的近似值。睡眠状态概率分布的最终模型将会是以alph和beta均值作为系数的logistic函数。

Python实施

我再三思考模拟上面提到的细节，最终我开始用Python将它们变成现实。观察一手的结果会比阅读别人的经验贴有帮助得多。想要在Python中实施MCMC，我们需要用到PyMC3贝叶斯库，它省略了很多细节，方便我们创建模型，避免迷失在理论之中。

通过下面的这些代码可以创建完整的模型，其中包含了参数alpha 、beta、概率p以及观测值observed，step变量是指特定的算法，sleep_trace包含了模型创建的所有参数值。

with pm.Model() as sleep_model:
    
    # Create the alpha and beta parameters
    # Assume a normal distribution
    alpha = pm.Normal('alpha', mu=0.0, tau=0.05, testval=0.0)
    beta = pm.Normal('beta', mu=0.0, tau=0.05, testval=0.0)
    
    # The sleep probability is modeled as a logistic function
    p = pm.Deterministic('p', 1. / (1. + tt.exp(beta * time + alpha)))
    
    # Create the bernoulli parameter which uses observed data to inform the algorithm
    observed = pm.Bernoulli('obs', p, observed=sleep_obs)
    
    # Using Metropolis Hastings Sampling
    step = pm.Metropolis()
    
    # Draw the specified number of samples
    sleep_trace = pm.sample(N_SAMPLES, step=step);

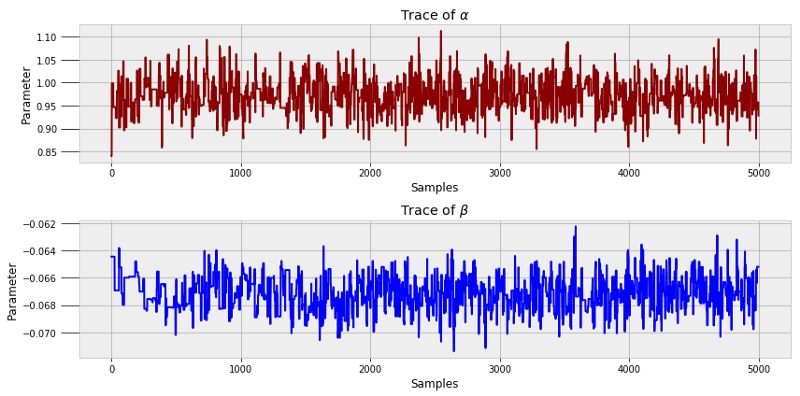
为了更直观地展现代码运行的效果，我们可以看一下模型运行时alpha和beta生成的值。

这些图叫做轨迹图，可以看到每个状态都与其历史状态相关，即马尔可夫链；同时每个值剧烈波动，即蒙特卡洛抽样。

使用MCMC时，常常需要放弃轨迹图中90%的值。这个算法并不能立即展现真实的分布情况，最初生成的值往往是不准确的。随着算法的运行，后产生的参数值才是我们真正需要用来建模的值。我使用了一万个样本，放弃了前50%的值，但真正在行业中应用时，样本量可达成千上万个、甚至上百万个。

通过足够多的迭代，MCMC逐渐趋近于真实的值，但是估算收敛性并不容易。这篇文章中并不会涉及到具体的估算方法（方法之一就是计算轨迹的自我相关性），但是这是得到最准确结果的必要条件。PyMC3的函数能够评估模型的质量，包括对轨迹、自相关图的评估。

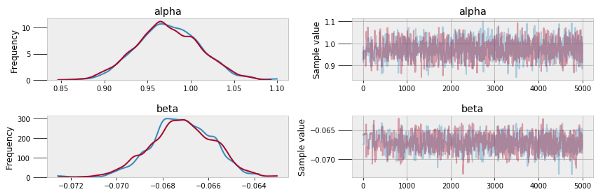
pm.traceplot(sleep_trace, ['alpha', 'beta'])
pm.autocorrplot(sleep_trace, ['alpha', 'beta'])

轨迹图（左）和自相关性图（右）

睡眠模型

建模、模型运行完成后，该最终结果上场了。我们将使用最终的5000个alpha和beta值作为参数的可能值，最终创建了一个单曲线来展现事后睡眠概率：

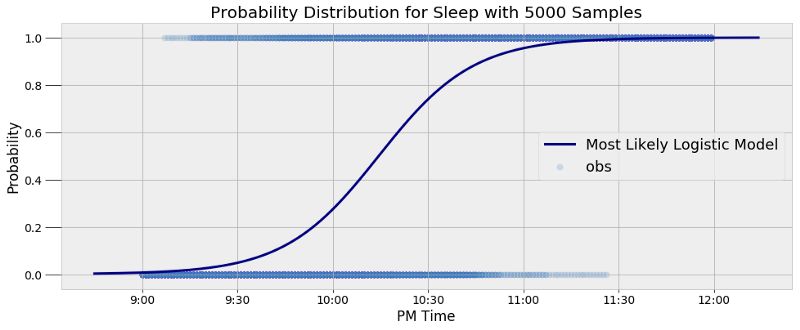
基于5000个样本的睡眠概率分布

这个模型能够很好的代表样本数据，并且展现了我睡眠模式的内在变异性。这个模型给出的答案并不是简单的“是”或“否”，而是给我们一个概率。举个例子，我们可以通过这个模型找出我在特定时间点睡觉的概率，或是找出我睡觉概率超过50%的时间点：

9:30  PM probability of being asleep: 4.80%.
10:00 PM probability of being asleep: 27.44%.
10:30 PM probability of being asleep: 73.91%.
The probability of sleep increases to above 50% at 10:14 PM.

虽然我希望在晚上10点入睡，但很明显大多时候并不是这样。我们可以看到，平均来看，我的就寝时刻是在晚上10:14。

这些值是基于样本数据的最有可能值，但这些概率值都有一定的不确定性，因为模型本身就是近似的。为了展现这种不确定性，我们可以使用所有的alpha、beta值来估计某个时间点的睡觉概率，而不是使用平均值，并且把这些概率值展现在图中。

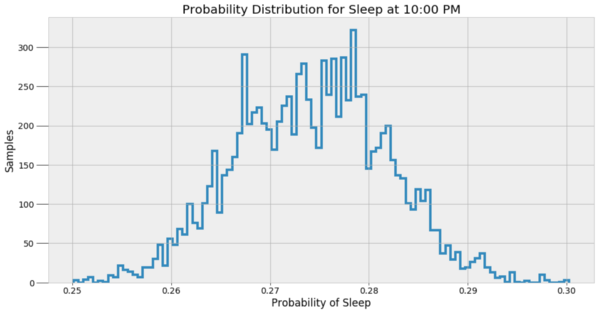
晚上10:00睡觉的概率分布

这些结果能够更好地展现MCMC模型真正在做的事情，即它并不是在寻找单一的答案，而是一系列可能值。贝叶斯推论在现实世界中非常有用，因为它是对概率进行了预测。我们可以说存在一个最可能的答案，但其实更准确的回复应当是：每个预测都有一系列的可能值。

起床模型

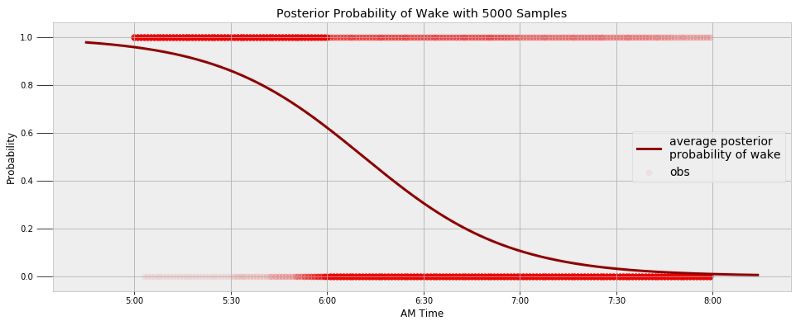
同样我可以用我的起床数据创建类似的模型。我希望能够在闹钟的帮助下总能在早上6:00起床，但实际上并不如此。下面这张图展现了基于观测值我起床的最终模型：

基于5000个样本的起床事后概率

可以通过模型得出我在某个特定时间起床的概率，以及我最有可能起床的时间：

Probability of being awake at 5:30 AM: 14.10%. 
Probability of being awake at 6:00 AM: 37.94%. 
Probability of being awake at 6:30 AM: 69.49%.
The probability of being awake passes 50% at 6:11 AM.

看来我需要一个更生猛的闹钟了….

睡眠的时间

出于好奇以及实践需求，最后我想创建的模型是我的睡眠时间模型。首先，我们需要寻找到一个描述数据分布的函数。事先，我认为应该是正态函数，但无论如何我们需要用数据来证明。

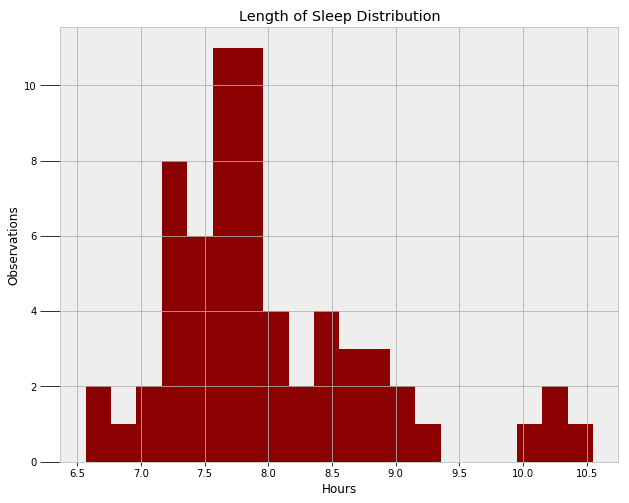
睡眠时间长短分布

正态分布的确能够解释大部分数据，但是图中右侧的异常值却无法得到解释（当我睡懒觉的时候）。我们可以用两个单独的正态分布来代表两种模式，但我要用偏态分布。偏态分布有三个参数：平均值、偏离值，以及alpha倾斜值。这三个参数的值都需要从MCMC算法中得到。下面的代码创建了模型，并且使用了Metropolis Hastings抽样。

with pm.Model() as duration_model:
    # Three parameters to sample
    alpha_skew = pm.Normal('alpha_skew', mu=0, tau=0.5, testval=3.0)
    mu_ = pm.Normal('mu', mu=0, tau=0.5, testval=7.4)
    tau_ = pm.Normal('tau', mu=0, tau=0.5, testval=1.0)
    
    # Duration is a deterministic variable
    duration_ = pm.SkewNormal('duration', alpha = alpha_skew, mu = mu_, 
                              sd = 1/tau_, observed = duration)
    
    # Metropolis Hastings for sampling
    step = pm.Metropolis()
    duration_trace = pm.sample(N_SAMPLES, step=step)

现在，我们可以使用三个参数的平均值来建立最有可能的分布模型了。下图为基于数据的最终偏态分布模型。

时长模型

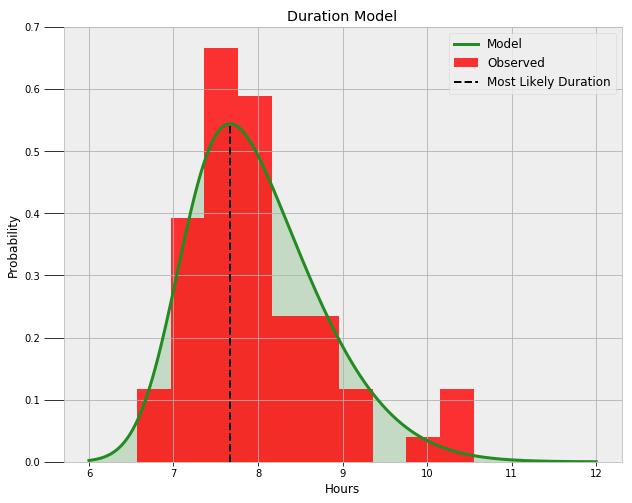
模型看上去很完美！通过模型可以找出我至少睡多长时长的可能性，以及我最经常的睡觉时长：

Probability of at least 6.5 hours of sleep = 99.16%.
Probability of at least 8.0 hours of sleep = 44.53%.
Probability of at least 9.0 hours of sleep = 10.94%.
The most likely duration of sleep is 7.67 hours.

结论

我想再次强调，完成这个项目让我体会到解决问题的重要性，尤其是有现实应用意义的项目！在我尝试使用马尔可夫链蒙特卡洛来端到端建立贝叶斯推论的时候，我重新熟悉了许多基础知识，并且非常享受这个过程。

我不仅了解到自身需要改进的习惯，而且当别人在谈论MCMC和贝叶斯推论时，我终于真的明白他们在谈论什么了！数据科学正是关于持续不断地在你自己的知识库中输入新的工具，而这最有效的办法就是发现一个问题，然后应用你所学的去解决问题！

原文链接：

https://towardsdatascience.com/markov-chain-monte-carlo-in-python-44f7e609be98

【今日机器学习概念】

Have a Great Definition

早鸟优惠倒计时第2天

数据科学实训营第5期

优秀助教推荐|土豆

现今纷纷扰扰的数据科学培训市场，是不是早已让你眼花缭乱，无处落足，还没有找到组织？不必慌张，土豆老司机拉住你的手，语重心长的要为你指条明道：究竟优质的数据科学教育培训是什么样的？

课程干货满满还不失风趣，讲师精力充沛还热爱分享，助教认真批改还热情反馈。

没错！数据科学实训营就是这样的明星课程！从基础的 Python 编程和Scrapy爬虫，到熟练运用 Numpy/Pandas/Matplotlib/Seaborn/Scikit-learn 等多种Python库，打通机器学习的任督二脉，在真实的数据科学竞赛案例和数据挖掘项目的打磨下，完成从数据科学小白到骨灰级玩家的华丽转变！

作为第4/5期的实训营助教，寄语小白学员：坚持跟上课程进度，按时完成所有作业，认真做好学习笔记，最终一定可以实现轻松入门数据科学哈！

志愿者介绍